Начальные понятия
Существуют различные подходы к определению понятия расстояния между точками. Например, в учебниках А.Н. Колмогорова, изданных во второй половине XX века, это понятие определяется аксиоматически, а длиной отрезка называется расстояние между его концами. В современных учебниках понятие «расстояние между точками», как правило, определяется через понятие «длина отрезка». Рассмотрим начальные понятия из курсов планиметрии и стереометрии.
| Отрезок | – геометрическая фигура, которая состоит из двух точек прямой и всех её точек, лежащих между данными точками. Эти точки называются концами отрезка |
| Равные отрезки | – отрезки, которые при наложении совмещаются |
| Середина отрезка | – точка, делящая его на два равных отрезка |
| Длина отрезка | – геометрическая величина, соответствующая отрезку, обладающая следующими свойствами: 1) При выбранной единице измерения каждый отрезок имеет длину, которая больше нуля; для любого положительного числа существует отрезок, длина которого выражается этим числом. 2) Равные отрезки имеют равные длины; отрезки, имеющие равные длины, равны. 3) Длина отрезка равна сумме длин отрезков, на которые он делится любой точкой. Метр – одна из множества имеющихся единиц измерения длины, соответствующая длине пути, проходимого светом в вакууме за (1/299 792 458) секунды (принято в 1983 г., до этого 1 метр определяли иначе – изучите историю вопроса самостоятельно!). Длина отрезка есть результат его сравнения с отрезком мерой 1 метр и его частями (1 см = 1/100 м - сантиметр, 1 мм = 1/1000 м – миллиметр и т.д.), т.е. результат, полученный в процессе измерения. На практике длину отрезка определяют с помощью линейки |
| Перпендикуляр к прямой (плоскости) | – отрезок прямой, проходящей через данную точку перпендикулярно данной прямой (плоскости), одним из концов которого является точка пересечения этих прямых (прямой и плоскости); эту точку пересечения называют основанием перпендикуляра. |
| Ортогональная проекция точки на прямую (на плоскость) | – основание перпендикуляра, проведённого из этой точки к данной прямой (плоскости) |
| Ортогональная проекция геометрической фигуры на плоскость | – геометрическая фигура, состоящая из проекций всех точек данной фигуры на данную плоскость |
| Наклонная к прямой (плоскости) | – отрезок, соединяющий тот конец перпендикуляра, который не лежит на данной прямой (в данной плоскости), с точкой этой прямой (плоскости), не совпадающей с основанием перпендикуляра (эту точку называют основанием наклонной). |
| Проекция наклонной на прямую (на плоскость) | – отрезок, соединяющий основания перпендикуляра и наклонной, проведённых к этой прямой (плоскости) |
1.1 Понятие расстояния в пространстве
Определение 1. Расстоянием между двумя точками называется длина отрезка, соединяющего данные точки.
Определение 2. Расстоянием между двумя геометрическими фигурами F 1и F 2(если оно существует)называется наименьшее из расстояний между двумя точками, одна из которых принадлежит фигуре F 1, а другая – фигуре F 2. Обозначается 
.
Если геометрические фигуры имеют общую точку, то расстояние между ними принимается равным 0.
Примеры. 1) Расстояние от центра сферы до этой сферы равно её радиусу.
2) Расстояние от центра шара до этого шара равно нулю.
3) Пусть дан шар (О; R) без границы и точка А, такая, что OA > R. Расстояние от точки А, до такого шара не существует.
Теорема 1. Расстояние от точки, не лежащей на прямой, до этой прямой равно длине перпендикуляра, проведенного из данной точки к данной прямой.
Дано: прямая a, точка M, M Ï a;
прямая b ^ a, M Î b, b Ç a = M 1.
Доказать: r (M; a) = MM 1.
Доказательство.
1) 
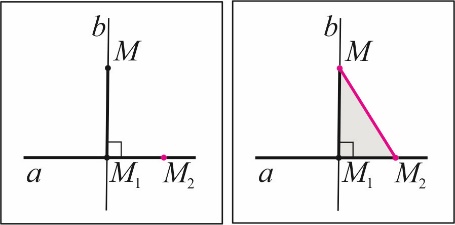На прямой a выберем произвольную точку M 2.
2) В D MM 1 M 2 (Ð M 1 = 90°) катет MM 1 меньше гипотенузы MM 2.
3) Длина отрезка MM 1 – наименьшее из расстояний между точкой M и точками прямой a, следовательно, по определению расстояния между геометрическими фигурами, r (M; a) = MM 1.‡
Задача 1. Найдите расстояние от точки M до луча AB, если расстояние от точки M до прямой AB равно 3 см, а проекция точки M на эту прямую не лежит на луче AB и удалена от его начала на 4 см.
Решение оформить самостоятельно.
Теорема 2. Расстояние от точки, не лежащей на плоскости, до этой плоскости равно длине перпендикуляра, проведенного из данной точки к данной плоскости.
Доказательство оформить самостоятельно.
‡
Теорема 3. Расстояние между двумя параллельными плоскостями равно расстоянию между произвольной точкой одной плоскости и другой плоскостью.
Дано: плоскости a, b; a || b;
точка A Î b;
Доказать: r (a; b) = r (A; a).
Доказательство.
1) 
По теореме 2 расстояние r (A; a) = AA 1, где AA 1 ^ a, A 1 Î a.
2) Пусть B – произвольная точка плоскости b, отличная от точки A. По теореме 2 расстояние r (B; a) = BB 1, где BB 1 ^ a, B 1 Î a.
3) Т.к. AA 1^a, BB 1^a, то AA 1 || BB 1 по признаку параллельных прямых, тогда AA 1 = BB 1, как отрезки параллельных прямых, заключенные между параллельными плоскостями.
4) Длина отрезка AA 1 – наименьшее из расстояний между точками плоскостей a и b, следовательно, по определению расстояния между геометрическими фигурами, r (a; b) = r (A; a).‡
Следствие 1. Расстояние от любой геометрической фигуры, лежащей в одной из параллельных плоскостей, до другой плоскости равно расстоянию между этими плоскостями.
Следствие 2. Расстояние от прямой до параллельной ей плоскости равно расстоянию от произвольной точки этой прямой до плоскости.
Основываясь на теореме 3, можно найти расстояние между двумя геометрическими фигурами, лежащими в параллельных плоскостях, в случае, если их проекции на одну из плоскостей пересекаются.
Типовые задачи, соответствующиерассмотренным понятиям
| Типовая задача | Алгоритм решения |
| Т1. Найти расстояние между точкой и прямой (точкой и плоскостью; двумя плоскостями; прямой иплоскостью) | 1) Определить вид взаимного расположения данных геометрических фигур. 2) Если точка лежит на прямой (точка лежит в плоскости; плоскости пересекаются; прямая и плоскость пересекаются), то сделать вывод, что искомое расстояние равно 0. В противном случае найти перпендикуляр, проведённый из данной точки к данной прямой (из данной точки к плоскости; из любой точки данной прямой к плоскости; из любой точки одной плоскости к другой плоскости). 3) Рассмотреть найденный перпендикуляр в контексте некоторой плоской геометрической фигуры и найти его длину |
| Т2. Построить прямую, проходящую через точку, не лежащую в плоскости и перпендикулярную этой плоскости (ЭСО «Стереометрия» / Глава 3 /§1/Опорные задачи/Вспомогательные ресурсы /Задача 17) | 1) В данной плоскости выбрать произвольную прямую. 2) Через данную точку провести плоскость, перпендикулярную выбранной прямой, и найти прямую пересечения построенной и данной плоскостей. 3) Через данную точку провести прямую, перпендикулярную прямой пересечения плоскостей. Эта прямая – искомая |
| Т3. Построить перпендикуляр из точки, не лежащей на данной прямой, к этой прямой (ЭСО «Стереометрия» / Глава 3 /§2/Опорные задачи/Вспомогательные ресурсы /Задача 19) | 1) Найти плоскость, содержащую данную прямую, и построить ортогональную проекцию данной точки на эту плоскость. 2) В рассматриваемой плоскости построить перпендикуляр из проекции данной точки к данной прямой. 3) Отрезок, соединяющий основание построенного перпендикуляра и данную точку, – искомый |
Задача 2. Боковое ребро FB пирамиды FABCD, основанием которой служит прямоугольник ABCD (Ð ACD =60°), перпендикулярно плоскости основания, его длина равна 3 см. Найдите расстояние от вершины F до диагонали AC, если расстояние от вершины F до стороны AD равно 
см. (ЭСО «Стереометрия» / Глава 3 / §2 / Примеры решений задач /Вспомогательные ресурсы /Задача 1)
Задача 3. Все рёбра прямого параллелепипеда ABCDA 1 B 1 C 1 D 1 равны между собой, Ð BAD =30°, точка O - середина ребра CC 1. Вычислите расстояние от точки C до плоскости AOD, если периметр сечения параллелепипеда плоскостью AOD равен 
см. (ЭСО «Стереометрия» / Глава 3 / §3 / Примеры решений задач /Вспомогательные ресурсы /Задача 2)
Опорные задачи, связанные с рассматриваемыми понятиями
О1. Если вершины основания пирамиды равноудалены от вершины пирамиды (боковые рёбра равны), то основание перпендикуляра, проведённого из вершины пирамиды к плоскости основания, совпадает с центром окружности, описанной около основания пирамиды. (ЭСО «Стереометрия» / Глава 3 / §2 /Опорные задачи / Учебные задания /Задача 14).
О2. Если стороны основания пирамиды равноудалены от вершины пирамиды (высоты боковых граней пирамиды равны), то основание перпендикуляра, проведённого из вершины пирамиды к плоскости основания, совпадает с центром окружности, вписанной в основание пирамиды. (ЭСО «Стереометрия» / Глава 3 / §2 /Опорные задачи / Учебные задания /Задача 15).
1.2 Расстояние между скрещивающимися прямыми
При изучении темы «Параллельность плоскостей» было доказано, что через две скрещивающиеся прямые a и b можно провести две параллельные плоскости a и b (a Ì a, b Ì b), и притом такая пара плоскостей единственная.
Теорема 4. Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, каждая из которых содержит одну из двух данных скрещивающихся прямых.
Дано: прямые a и b; плоскости a, b; a || b; a Ì a, b Ì b.
Доказать: r (a; b) = r (a; b).
Доказательство.
1) Пусть A – произвольная точка прямой b. Т.к. A Î b и b Ì b, то A Î b. По теореме 3 расстояние r (a; b)= AA 1, где AA 1 ^ a, A 1 Î a, то есть длина отрезка AA 1 – наименьшее из расстояний между двумя точками, одна из которых принадлежит плоскости a, а другая – плоскости b. Докажем, что существует отрезок CC 1 = AA 1, один из концов которого принадлежит прямой a, а второй – прямой b.
2) Зададим плоскость g= (b; AA 1), g Ç a = c, c Ç a = C 1. Проведём прямую C 1 C || AA 1, С Î b.
3) Т.к. C 1 C || AA 1 (по построению) и c || b (т.к. плоскость g проходит через прямую b || a), то AA 1 C 1 C – параллелограмм, следовательно, по свойству параллелограмма CC 1= AA 1.
4) Т.к. точка C Î b, точка C 1 Î a и CC 1 = AA 1, то CC 1– наименьший из отрезков, один из концов которого лежит на прямой a, а второй – на прямой b, следовательно, расстояние r (a; b) = r (a; b).‡
Т.к. CC 1 || AA 1 и AA 1 ^ a, AA 1 ^ b, то СС 1 ^ a, СС 1 ^ b.
Определение 3. Общим перпендикуляром двух скрещивающихся прямых называется перпендикулярный им отрезок, концы которого лежат на данных прямых.
Докажите самостоятельно единственность общего перпендикуляра к двум скрещивающимся прямым
‡
Следствие 1. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.
Следствие 2. Расстояние между скрещивающимися прямыми равно расстоянию от одной из скрещивающихся прямых до плоскости, проходящей через другую прямую и параллельной первой прямой.
Типовые задачи по теме «Расстояние между скрещивающимися прямыми»
| Типовая задача | Алгоритм решения |
| Т4. Вычислить расстояние между скрещивающимися прямыми | 1 алгоритм 1) Найти параллельные плоскости, каждая из которых содержит одну из скрещивающихся прямых. 2) Выбрать на одной из плоскостей точку и провести из неё перпендикуляр ко второй плоскости. 3) Вычислить длину перпендикуляра. 2 алгоритм 1) Найти общий перпендикуляр двух скрещивающихся прямых. 2) Вычислить длину перпендикуляра. 3 алгоритм 1) Найти плоскость, проходящую через одну из скрещивающихся прямых и параллельную второй прямой. 2) Выбрать на второй прямой точку и провести из неё перпендикуляр к построенной плоскости. 3) Вычислить длину перпендикуляра |
Задача 4. Дан куб ABCDA 1 B 1 C 1 D 1, длина ребра которого равна 2. Вычислите расстояние между следующими прямыми: а) AB 1 и D 1 C; б) D 1 C и AD; в) AD и MN, где M и N – середины рёбер AA 1 и A 1 B 1 соответственно.
Опорные задачи, связанные с вычислением расстояния между скрещивающимися прямыми
О3. Вычислите расстояние между непересекающимися рёбрами тетраэдра, длина ребра которого равна 
(Реконструирование опорной геометрической конструкции: рассмотреть«тетраэдр в контексте куба»).
О4. Докажите, что объём треугольной пирамиды можно найти по формуле 
, где a и b – длины двух скрещивающихся рёбер этой пирамиды, d – расстояние между ними, j – угол между прямыми, содержащими эти скрещивающиеся рёбра.
Рассмотрим треугольную пирамиду DABC в контексте параллелепипеда AVCXYDZB, диагоналями граней которого служат рёбра данной пирамиды. Пусть AC = a, BD = b, Ð(AC; BD) = j, r(AC; BD)= d.
1) Объём пирамиды DABC равен разности объёма параллелепипеда AVCXYDZB и объёмов пирамид AYDB, CBDZ, BAX C, DAVC, отсекаемых от параллелепипеда плоскостями граней пирамиды DABC.
2) Перечисленные пирамиды равновелики, так как равны площади их оснований и высоты, проведённые к основаниям. Кроме того, объем каждой их них равен 
объёма параллелепипеда, например: 
, h =r(B; ACX).
3) 
.
4) 
= SAVCX × h = 
. Учитывая, что VX = BD = b, Ð COX =Ð(AC; BD) = j; h = r(AC; BD)= d, то 
.‡
Метод вспомогательного объема при вычислении расстояний в пространстве
Суть метода вспомогательного объёма для вычисления расстояний в пространстве.
1. По аналогии с методом площадей объём рассматриваемой пирамиды выражают дважды: через искомое расстояние и любым другим способом.
2. Приравняв полученные выражения объёма, находят искомое расстояние.
Задача 5. Дан куб АВСDA 1 B 1 C 1 D 1и точка N – середина ребра AA 1. Вычислите расстояние между прямыми AB 1 и DN, если длина ребра куба равна а.
Решение методом вспомогательного объёма
1) 
Рассмотрим пирамиду ANB 1 D. Её объём 
, где d = r(AB 1; DN), j = Ð(AB 1; DN). Иначе 
.
2) Имеем: 
. В этом равенстве 
; 
. Найдём значение sinj.
3) DC 1 || AB 1, следовательно, по определению угла между скрещивающимися прямыми, j = Ð(DC 1; DN)
4) В треугольнике DNC 1 (
; 
; 
) по теореме косинусов 
= 
= 
, тогда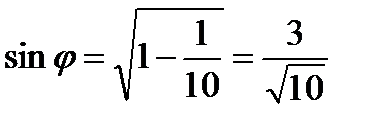 
.
5) Решая относительно d уравнение 
находим 
.
Ответ: 
.