Вопросы построения и использования эконометрических моделей рассмотрим более подробно на примере линейных регрессионных моделей как в случае парной регрессии (однофакторная модель), так и в случае множественной регрессии (многофакторная модель); в последнем случае будем рассматривать модели множественной регрессии на примере линейной двухфакторной модели.
Основу математического аппарата для рассматриваемых моделей составляют такие разделы математической статистики, как корреляционный и регрессионный анализ. Для определенности эндогенные переменные в этих моделях будем называть результативными признаками и обозначать их, как и ранее, буквой у, а экзогенные переменные будем называть факторными признаками и обозначать их буквой х. Методы корреляционно-регрессионного анализа позволяют решать три основные задачи: определение формы связи между результативным и факторными признаками, измерение тесноты связи между ними, анализ влияния отдельных факторных признаков. Рассмотрим решение этих задач для указанных видов эконометрических моделей; при этом для наглядности будем иллюстрировать выводы на конкретном примере экономического анализа.
В табл. 7.1 представлены статистические данные о расходах на питание, душевом доходе и размере семьи для девяти групп семей. Требуется проанализировать зависимость величины расходов на питание от величины душевого дохода и размера семьи. В соответствии с этим первый показатель будет результативным признаком, который обозначим у, а два других будут факторными признаками, или просто факторами, и мы их обозначим соответственно x 1 и x 2.
Таблица 7.1
| Номер группы | Расход на питание (у) | Душевой доход (x 1) | Размер семей (х2) |
| 1,5 | |||
| 2,1 | |||
| 2,7 | |||
| 3,2 | |||
| 3,4 | |||
| 3,6 | |||
| 3,7 | |||
| 4,0 | |||
| 3,7 |
Рассмотрим сначала однофакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (x 1). Она выражается линейной функцией вида
|
|
(7.1)
параметры которой а0 и a 1, находятся в результате решения системы нормальных уравнений, которая в свою очередь формируется, как уже отмечалось в главе 5, на основе метода наименьших квадратов. Система нормальных уравнений для рассматриваемого случая аналогична системе (5.5) и имеет вид
(7.2)
где суммирование проводится по всем п группам. Используя данные табл. 7.1, получим систему уравнений:
решением которой являются значения а0= 660,03; a 1 = 0,11. Таким образом, модель имеет вид
(7.3)
Уравнение (7.3) называется уравнением регрессии, коэффициент a 1, - коэффициентом регрессии. Направление связи между у и x 1 определяет знак коэффициента регрессии а1, в нашем случае данная связь является прямой. Теснота этой связи определяется коэффициентом корреляции (парным):
(7.4)
в этой формуле Sy - средняя квадратическая ошибка выборки у из табл. 7.1:
где 
- средняя арифметическая значений у,
- средняя квадратическая ошибка уравнения (7.3) для числа степеней свободы п - 2:
где 
- соответствующее значение расходов на питание, вычисленное по модели (7.3).
В этих формулах, как и ранее, суммирование ведется по всем группам от 1 до п.
Чем ближе значение коэффициента корреляции к единице, тем теснее корреляционная связь. В нашем примере 
следовательно,
|
|
Полученное значение 
свидетельствует, что связь между расходами на питание и душевым доходом очень тесная.
Величина 
называется коэффициентом детерминации и показывает долю изменения (вариации) результативного признака под действием факторного признака. В нашем случае 
; это означает, что фактором душевого дохода можно ооъяснить почти 86% изменения расходов на питание.
Коэффициенты регрессии (в рассматриваемом случае это коэффициент а 1) нельзя использовать для непосредственной оценки влияния факторов на результативный признак из-за различия единиц измерения исследуемых показателей. Для этих целей вычисляются коэффициенты эластичности и бета-коэффициент.
Коэффициент эластичности для рассматриваемой модели парной регрессии рассчитывается по формуле
(7.5)
Он показывает, на сколько процентов изменяется результативный признак у при изменении факторного признака x 1 на один процент.
В нашем примере коэффициент регрессии а 1 равен 0,11, а средние арифметические 
и 
равны соответственно 6080,6 и 1313,9.
Поэтому коэффициент эластичности расходов на питание в зависимости от душевого дохода будет равен
Это означает, что при увеличении душевого дохода на 1% расходы на питание увеличатся на 0,51%.
Бета-коэффициент в нашем случае задается формулой
(7.6)
где 
и 
- средние квадратические ошибки выборки величин х 1 и у из табл. 7.1 соответственно.
Величина 
уже была рассчитана ранее и равна 454 070, поэтому величина Sу равна 673,8; аналогичные расчеты дают значение величины 
, равное 4242,0. Бета-коэффициент показывает, на какую часть величины своего среднего квадратического отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения.
|
|
В нашем случае получаем следующее значение бета-коэффициента:
т.е. увеличение душевого дохода на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения расходов на питание на 0,69 среднеквадратического отклонения этих расходов.
Рассмотрим теперь двухфакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х 1) и размера семей (х 2). Как уже отмечено выше, множественный (многофакторный) корреляционно-регрессионный анализ решает три задачи: определяет форму связи результативного признака с факторными, выявляет тесноту этой связи и устанавливает влияние отдельных факторов. В нашем случае эта модель имеет вид
(7.7)
Параметры модели а 0, а 1 и а 2 находятся путем решения системы нормальных уравнений:
(7.8)
Используя данные табл. 7.1, получим систему нормальных уравнений в виде
Решая эту систему (например, методом Гаусса), получим: а0 = -192,0; а1 = 0,072; а2 = 344,9, так что модель (7.7) имеет вид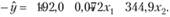 
Для определения тесноты связи предварительно вычисляются парные коэффициенты корреляции 
Например,
(7.9)
где черта над символами означает среднюю арифметическую, а Sy и Sx - средние квадратические ошибки соответствующих выборок из табл. 7.1:
Аналогичный вид имеют формулы для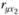 
и 
После этого вычисляют коэффициент множественной корреляции
(7.10)
который колеблется в пределах от 0 до 1; чем ближе он к 1, тем в большей степени учтены факторы, влияющие на результативный признак.
В нашем примере расчеты дают следующее значение коэффициента множественной корреляции: 
, что выше значения коэффициента корреляции в случае однофакторной модели. Таким образом, степень тесноты связи расходов на питание с факторами душевого дохода и размера семей является очень высокой.
Величина 
называется совокупным коэффициентом детерминации и показывает долю вариации результативного признака под воздействием изучаемых факторных признаков. В нашем примере 
; это означает, что совместное влияние душевого дохода и размера семей объясняет почти 97% изменения расходов на питание.
Задача анализа тесноты связи между результативным и одним из факторных признаков при неизменных значениях других факторов решается в многофакторных моделях при помощи частных коэффициентов корреляции. Так, частный коэффициент корреляции между результативным признаком у и факторным признаком х 1 при неизменном значении факторного признака х 2 рассчитывается по формуле
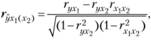(7.11)
где используются парные коэффициенты корреляции, рассчитываемые по формулам, аналогичным (7.9).
Аналогичная формула имеет место для частного коэффициента корреляции 
между результативным признаком у и факторным признаком х 2 при неизменном значении факторного признака х 1.
Для рассматриваемого примера частные коэффициенты корреляции расходов на питание от душевого дохода и размера семей составляют
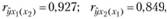
т.е. теснота связи между расходами на питание и одним из исследуемых факторов при неизменном значении другого является весьма значительной.
Если частные коэффициенты корреляции возвести в квадрат, то получим частные коэффициенты детерминации, показывающие долю вариации результативного признака под действием одного из факторов при неизменном значении другого фактора. В нашей задаче
следовательно, влиянием душевого дохода при неизменном размере семьи объясняется почти 86% изменения расходов на питание, а изменение размера семьи при неизменном душевом доходе объясняет более 72% изменения расходов на питание.
Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае линейной двухфакторной модели (7.7) рассчитываются по формулам
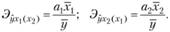(7.12)
Черта над символом, как и ранее, означает среднюю арифметическую. Частные коэффициенты эластичности показывают, на сколько процентов изменится результативный признак, если значение одного из факторных признаков изменится на 1%, а значение другого факторного признака останется неизменным.
В рассматриваемом примере а 1 = 0,072; а 2 = 344,9; 
= 1313,9; 
, следовательно, по формулам (7.12) получим:
Это означает, что при увеличении душевого дохода на 1% и неизменном размере семьи расходы на питание увеличатся на 0,333%, а увеличение (условное) на 1% размера семьи при неизменном душевом доходе приведет к возрастанию расходов на питание на 0,790%.
Определенные выводы о влиянии отдельных факторов на результативный признак в случае линейной модели множественной регрессии можно сделать на основе расчета частных бета-коэффициентов, которые для двухфакторной модели (7.7) задаются формулами
(7.13)
Частные бета-коэффициенты показывают, на какую долю своего среднеквадратического отклонения изменится в среднем результативный признак при изменении одного из факторных признаков на величину его среднеквадратического отклонения и неизменном значении остальных факторов.
В рассматриваемой задаче а 1 = 0,072; а 2 = 344,9; S y = 673,8; 
= 4242,0; 
= 0,79, так что расчеты по формулам (7.12) дают следующие значения частных бета-коэффициентов:
Это означает, что при неизменном составе семей увеличение на величину своего среднеквадратического отклонения размера душевого дохода приведет к увеличению среднего значения расходов на питание на 0,45 их среднеквадратического отклонения, а при неизменном душевом доходе увеличение размера семей на величину его среднеквадратического отклонения приведет к возрастанию расходов на питание лишь на 0,40 их среднеквадратического отклонения.