Будем рассматривать, как и в предыдущем параграфе, линейные эконометрические модели регрессии. Их качество оценивается стандартным для экономико-математических моделей образом: по адекватности и точности. Адекватность регрессионных моделей может быть установлена, как и в случае трендовых моделей, на основе анализа остаточной последовательности; при этом расчетные значения получаются подстановкой в модель фактических значений всех включенных в модель факторов. Остаточная последовательность проверяется на выполнение свойств случайной компоненты временного экономического ряда: близость нулю математического ожидания, случайный характер отклонений, отсутствие автокорреляции и нормальность закона распределения. Эта проверка проводится теми же методами и с использованием тех же статистических критериев, что и для трендовых моделей (см. параграф 5.2).
О качестве моделей регрессии можно судить также по значениям коэффициента корреляции (индекса корреляции) и коэффициента детерминации для однофакторной модели и по значениям коэффициента множественной корреляции и совокупного коэффициента детерминации для моделей множественной регрессии. Формулы расчета этих коэффициентов приведены в параграфе 7.2. Чем ближе абсолютные величины указанных коэффициентов к 1, тем теснее связь между изучаемым признаком и выбранными факторами и, следовательно, с тем большей уверенностью можно судить об адекватности построенной модели, включающей в себя наиболее влияющие факторы.
Для оценки точности регрессионных моделей обычно используются те же статистические критерии точности, что и для трендовых моделей, в частности, средняя относительная ошибка аппроксимации (см. формулу (5.14)). Проверка значимости модели регрессии проводится с использованием F -критерии Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели. Если расчетное значение этого критерия со степенями свободы v 1= n - 1 и v 2 = n - m - 1, где п - количество наблюдений и т - число включенных в модель факторов, больше табличного значения критерия Фишера при заданном уровне значимости, то модель признается статистически значимой.
При проверке качества регрессионной модели целесообразно оценить также значимость коэффициентов регрессии. Эта оценка проводится по i-статистике Стьюдента путем проверки гипотезы о равенстве нулю k -го коэффициента регрессии (k = 1, 2,..., т). Расчетное значение t критерия с числом степеней свободы (п - т - 1) находят путем деления k -гo коэффициента регрессии на среднеквадратическое отклонение этого коэффициента, которое в свою очередь вычисляется как квадратный корень из произведения несмещенной оценки дисперсии остаточной компоненты и k -гo диагонального элемента матрицы, обратной матрице системы нормальных уравнений относительно параметров модели. Это расчетное значение сравнивается с табличным значением критерия Стьюдента при заданном уровне значимости, и если оно больше табличного значения, коэффициент регрессии считается статистически значимым. В противном случае соответствующий данному коэффициенту регрессии фактор следует исключить из модели, при этом качество модели не ухудшится.
Перейдем к вопросу экономического прогнозирования на основе модели регрессии, при этом будем предполагать, что модель, построенная на базе временных рядов изучаемого показателя и включенных в модель факторов, является адекватной и достаточно точной. При использовании построенной модели для прогнозирования делается также предположение о сохранении существовавших ранее взаимосвязей переменных и на период упреждения.
Для прогнозирования зависимой переменной (результативного признака) на L шагов вперед необходимо знать прогнозные значения всех входящих в модель факторов. Эти значения могут быть получены на основе экстраполяционных методов, например, с использованием средних абсолютных приростов факторных признаков; они могут быть также определены методами экспертных оценок или непосредственно заданы исследователем экономического процесса. Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
Для определения области возможных значений результативного показателя при известных значениях факторов, т.е. доверительного интервала прогноза, необходимо учитывать два возможных источника ошибок. Ошибки первого рода вызываются рассеиванием наблюдений относительно линии регрессии, и их можно учесть, в частности, величиной среднеквадратической ошибки аппроксимации изучаемого показателя с помощью регрессионной модели. Обозначим эту величину 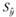 и вычислим ее по формуле, аналогичной (5.17).
и вычислим ее по формуле, аналогичной (5.17).
Ошибки второго рода обусловлены тем, что в действительности жестко заданные в модели коэффициенты регрессии являются случайными величинами, распределенными по нормальному закону. Эти ошибки учитываются вводом поправочного коэффициента при расчете ширины доверительного интервала; формула для его расчета включает табличное значение t -статистики при заданном уровне значимости и зависит от вида регрессионной модели.
Для линейной однофакторной модели, общий вид которой имеет структуру, аналогичную (7.1), величина отклонения от линии регрессии задается выражением (обозначим его R):
 (7.14)
(7.14)
Здесь п - число наблюдений, L - количество шагов вперед, а - уровень значимости прогноза, xt- наблюдаемое значение факторного признака в момент t,  - среднее значение наблюдаемого фактора, xn+L- прогнозное значение фактора на L шагов вперед.
- среднее значение наблюдаемого фактора, xn+L- прогнозное значение фактора на L шагов вперед.
Таким образом, для рассматриваемой модели формула расчета нижней и верхней границ доверительного интервала прогноза имеет вид
 (7.15)
(7.15)
где  означает точечную прогнозную оценку изучаемого результативного показателя по модели на L шагов вперед.
означает точечную прогнозную оценку изучаемого результативного показателя по модели на L шагов вперед.