Раздел 10. Начала математического анализа.
Тема 10.1 Производная.
Занятие №83. Лекция. Понятие производной
СОДЕРЖАНИЕ ЗАНЯТИЯ
Изучение нового материала
Вопросы (план)
Задачи, приводящие к понятию производной.
Определение производной.
3. Механический и геометрический смысл производной.
Примеры.
Задачи, приводящие к понятию производной.
|
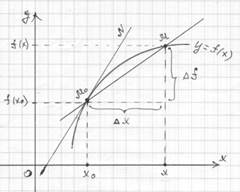
1) Пусть дан график f(x).
Рассмотрим точку М0 с абсциссой xo. Пусть ∆х - это изменение абсциссы от точки xo до х, т.е. ∆х = х - xo , M0М – секущая, M0N – касательная.
Найдите
а) угловой коэффициент секущей (это средняя скорость изменения функции);
б) угловой коэффициент касательной (подсказка: касательная - это предельное положение секущей)
Решение: f(x) – заданная функция, ∆х = х - xo – изменение абсциссы от точки xo до х
vср = 
. В нашем случае kсек = 
При х→х0 (или ∆х →0) будет f(x)→f(x0), следовательно, M0М→ M0N. Тогда k кас =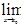 
.
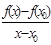А а вы знаете, кто впервые стал использовать знак «∆» для обозначения разности аргументов? Буква «∆»(дельта) одна из заглавных букв греческого алфавита ее стал использовать Эйлер (середина 18 века).
2) Рассмотрим движение материальной точки М по прямой с выбранным на ней началом отсчета - точкой О. Расстояние от начала отсчета до точки М в каждый момент времени t обозначим буквой s.Тогда движение точки М будет описываться функцией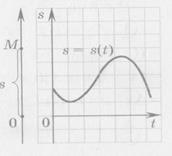 
s = s (t), t 
[ t0; t ].
Найдите:
а) среднюю скорость за отрезок [ t0; t ];
б) скорость точки в момент времени t0 (мгновенную скорость).
Решение: За промежуток времени длительности t - t0 между моментами времени t0 и t точка проходит путь равный s (t) –s(t0).
Среднюю скорость получают, разделив перемещение материальной точки s на изменение времени, в течение которого оно совершено.
Тогда vср =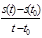 
;
Чем меньше рассматриваемый промежуток времени, тем точнее можно охарактеризовать движение. А мгновенной скоростью называется предел средней скорости за промежуток времени от t0 до t при t→ t0. Тогда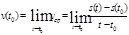 
Определение производной.
Подобные задачи рассматриваются и в экономике, и в анализе ценовой политики. Например: «цена товара напрямую зависит от расходов на производство» или «объем реализации некоторой продукции зависит от роста или снижения его цены».
А теперь давайте подведём итоги вашей исследовательской работы. Мы рассмотрели 2 задачи, но все они привели к одной и той же математической модели: к пределу отношения разности значений функции к разности значений аргумента. В русском языке для величины, на которую изменилось начальное количество, используется слово «прирост».
Так как ∆х показывает на сколько изменилось начальное значение аргумента х0,то ∆х называют «приращением аргумента».
Приращению аргумента соответствует «приращение функции», которое также обозначается с помощью заглавной греческой буквы «∆». Исходя из этого полученную формулу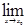 
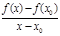можно записать по-другому: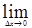 
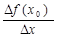или 
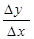и прочитать так: предел отношения приращения функции к приращению аргумента при ∆х →0 (или при ∆ t→0).
Поскольку многие задачи в различных областях науки в процессе решения приводят к такой же модели - этому пределу надо: дать название, дать обозначение и изучить его. Это мы с вами сейчас и сделаем.
Математически предел отношения приращения функции к приращению аргумента при ∆х→0 называется производной в точке xo,но обозначается по-разному:
f′(х), f′, 
у′ - эти обозначения для производной ввел Жозеф Луи Лагранж
или 
- эти обозначения ввел Готфрид Вильгельм Лейбниц (разности xo - xo и у - уo он обозначил как dx и dy, d – первая буква в латинском слове diferentia означающее «разность»). В своих трудах он писал:«…Предупреждаю, чтобы остерегались отбрасывать dx, - ошибка, которую часто допускают и которая препятствует продвижению вперед…» Это определение вы запишете в тетрадях.
Пусть функция f(x) определена в точке xo и в некоторой её окрестности.
Дадим точке xo приращение ∆х. Тогда производной в точке xo называется предел отношения приращения функции к приращению аргумента при ∆х →0
а именно: f′(х0) =lim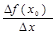
|
Теперь посмотрите на наши задачи и сформулируйте план нахождения производной.
1. Задать функцию f(x).
2. Задать приращение аргументу и найти приращение функции ∆у = f(x0 +∆х) – f(x0).
3. Найти отношение приращения функции к приращению аргумента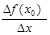 
4. Найти предел отношения приращения функции к приращению аргумента при ∆х→0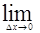 
.
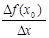3. Механический и геометрический смысл производной.
Механический смысл производной – это скорость изменения расстояния: s'(t) = v(t);
Геометрический смысл: f'(хо) – это коэффициент угла наклона касательной к оси Ох
f'(хо) = k = tg α.
Т.е. из геометрического смысла получается, что если существует производная в точке хо, то можно провести что?
| …Если существует производная в точке хо, то можно провести касательную в точке хо. Наоборот - если можно провести касательную в точке хо, то в этой точке существует производная. |
|
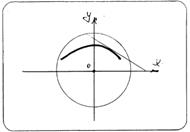
Итак, подведём итог: мы ознакомились с определением производной, но встаёт вопрос: а всегда ли существует производная в точке? Посмотрите на рисунок. На нём вы видите график некоторой функции у = f(x). А теперь давайте мысленно «покрутим» окружность с графиком вокруг центра и рассмотрим различные положения кривой и касательной к ней.
Рассмотрите различные случаи. Особое внимание обратите на моменты, когда касательная перпендикулярна оси Ох и параллельна оси Ох. Всегда ли существует ли производная в точке хо?
| Если касательная к графику функции будет убывающей, то каким будет угол между этой прямой и осью Ох? | Угол будет тупым. |
| Каким будет угловой коэффициент k? | k < 0 |
| Если касательная к графику функции будет возрастающей, то каким будет угол между этой прямой и осью Ох? | Угол будет острым. |
| Каким будет угловой коэффициент k? | k > 0 |
| Если касательная к графику функции будет параллельна оси Ох или совпадать с ней, то каким будет угол между этой прямой и осью Ох? | Угла не будет, вернее α = 0º |
| Чему равен тангенс угла наклона такой касательной? | tg 0º = 0 |
| Чему равен угловой коэффициент k касательной, параллельной оси Ох? | Также не существует! |
| Чему равен угол наклона вертикальной касательной? | α = 90º |
| Чему равен тангенс угла наклона вертикальной касательной? | tg 90º не существует. Почему?Потому, что cos 90º = 0… |
| Чему равен угловой коэффициент k вертикальной касательной? | Также не существует! |
Давайте вернёмся к геометрическому смыслу производной: производная в точке равна угловому коэффициенту касательной, проведённой в этой точке f'(хо) = k = tg α.
Мы получили, что не во всех точках существует производная.
Как же так? Мы же определили, что если есть касательная в точке, то в точке есть и производная! И вот пример: есть касательная, но нет производной?! Оказывается:
| Если в точке можно провести невертикальную касательную, то в этой точке существует производная, и наоборот, если в точке существует производная, то в этой точке можно провести невертикальную касательную |
Примеры.
|
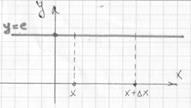
Пример № 1: Пользуясь определением и схемой вычисления производной, найдите производную функции y = C.
Решение
y = C – постоянная линейная функция.
∆у = f(x +∆х) – f(x)= С – С = 0; 
= 0,
то у′ = 
= 
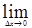
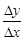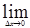
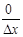= 0.
Итак, (С) ′= 0.
|
Пример №2: Пользуясь определением и схемой вычисления производной, найдите производную функции y = kx + b.
Решение
y = kx + b – линейная функция.
Аргументу х дадим приращение ∆х, тогда
∆у = f(x + ∆х) – f(x)=
= k (x +∆х) – (kx + b) = k∙x + k∆∙х – kx - b = k∆∙х
= 
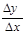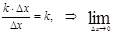k = k.
Итак, (kx + b)′ = k.
|
Пример №3: Пользуясь определением и схемой вычисления производной, найдите производную функции y = х2.
Решение
y = х2.
Аргументу х дадим приращение ∆х, тогда
∆у = f(x + ∆х) – f(x)=
= (x +∆х)2 – х2 =
= х2+ 2∙х∙∆х + (∆х)2 - х2 = 2∙х∙∆х + (∆х)2 = ∆х∙(2х +∆х)
= 
2х = 2х.
Итак, (х2)′ = 2х.
Вопросы для закрепления изученного материала:
1. Что такое приращение аргумента, приращение функции?
2. Как определяют приращение функции в заданной точке?
3. Дать определение производной.
4.Выполнить задания из учебника № 4.6 устно, 4.7, 4.11, 4.13, 4.14
Вопросы для самостоятельного изучения:
ОИ2. П.4.1 – 3.2 прочитать, выполнить № 4.8(а, б), 4.12.
Информационное обеспечение обучения:
ОИ2. Алгебра и начала математического анализа. 11 класс: учебник для общеобразовательных организаций: базовый и углублённый уровни / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др. – Москва: Просвещение, 2014. – 464 с.