В большинстве исследований динамических явлений в экономике в качестве важнейшего фактора, определяющего развитие экономической системы в модели, вводится временной фактор (тренд). Процедура экстраполяции тенденций предполагает построение трендовых моделей прогнозирования.
Методика построения экстраполяционных моделей прогнозирования
товарных рынков
Основные этапы:
1Выбор аппроксимирующего полинома и его параметров для данного временного ряда объемов производства готовых изделий.
2 Оценка выбранного полинома (тренда Ut) и нахождение случайной составляющей Et
.
3Проверка соответствия распределения остаточной компоненты нормальному закону распределения.
4Проверка равенства математического ожидания значения остаточной компоненты нулю.
5Проверка независимости значений ряда остаточной компоненты (оценка наличия автокорреляции)
6Проверка точности модели.
Краткое описание основных этапов
1 Выбор аппроксимирующего полинома и его параметров для данного временного ряда объемов производства готовых изделий.
1.1. Предположим, что между переменными существует линейная зависимость:
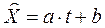(3.1)
Параметры a и b определяем методом наименьших квадратов:
(3.2)
Результаты расчета рекомендуется представить в виде таблицы 3.1.
Таблица 3.1
Процедура расчета показателей модели при линейной аппроксимации
| N п/п | ti | Xi | ti2 | Xi×ti | 
|
| … | … | … | … | … | … |
| - | S | S | S | S | - |
В результате решения системы уравнений (3.2), вычислим значения параметров a и b и получим полином при линейной аппроксимации.
1.2. Предположим, что между переменными существует параболическая зависимость:
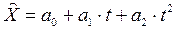(3.3)
Параметры а0; а1; а2 определяем по методу наименьших квадратов при решении системы уравнений:
(3.4)
Результаты расчета рекомендуется представить в виде таблицы 3.2.
Таблица 3.2
Процедура расчета показателей при аппроксимации параболической зависимостью
| N п/п | ti | Xi | ti2 | ti3 | ti4 | Xi×ti | Xi×ti2 |
|
| … | … | … | … | … | … | … | … | … |
| - | S | S | S | S | S | S | S | - |
В результате решения системы уравнений (3.4), вычислим значения параметров а0; а1; а2 и получим полином при параболической аппроксимации.
Проведем основанное на методе наименьших квадратов сравнение значений 
, полученных путем применения каждого из полиномов. Сущность метода наименьших квадратов заключается в том, что сумма квадратов отклонений, полученного значения (аппроксимирующего значения) от заданного значения Xi, должна быть минимальной.
Наиболее точный полином, соответствующий эмпирическим (заданным) значениям Xi, должен дать наименьшее значение этой суммы. Для сравнения рекомендуется построить таблицу 3.3.
Таблица 3.3
Сравнительная оценка моделей
| ti | 
| 
| ||||||
| Xi |
| 
| 
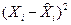
| Xi |
|
|
| |
| … | … | … | … | … | … | … | … | … |
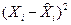
| - | - | - | - | S | - | - | - | S |
2 Оценка выбранного полинома (тренда Ut) и нахождение случайной составляющей Et
.
Предположим, что исследуемый ряд может быть записан следующим образом:
, (3.5)
где Ut – выбранный полином; Et – случайная составляющая.
Компонента Ut будет считаться найденной правильно только тогда, когда случайная компонента Et удовлетворяет следующим условиям, доказывающим, что она действительно носит случайный характер. Этих условий несколько:
а) условие случайности,
б) условие нормальности,
в) условие равенства нулю математического ожидания,
г) условие независимости.
Рассмотрим эти условия, подтверждающие адекватность выбранного полинома (тренда) и случайный характер составляющей Et, а также характеристики точности модели.