ФОРМУЛЫСТАТИСТИКИ
Средние величины
Среднее арифметическое
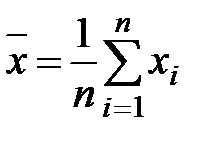(невзвешенное) для несгруппированных данных,
(взвешенное) для сгруппированных данных.
Среднее гармоническое
(невзвешенное),
(взвешенное), где 
.
Отыскание среднего арифметического через среднее гармоническое:
, где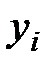 
– объем признака в группе: 
.
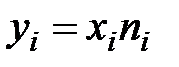Среднее геометрическое
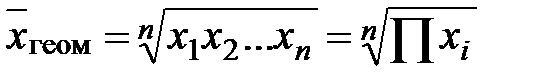(невзвешенное),
(взвешенное).
Среднее квадратическое
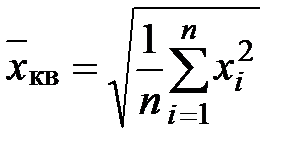(невзвешенное),
(взвешенное).
Структурные средние
Мода
Для дискретного вариационного ряда:
, где 
такое, что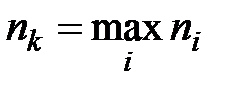 
,
Для интервального вариационного ряда (с интервалами равной длины):
.
Здесь 
– нижняя граница модального интервала, 
– длина модального интервала, 
– частота модального интервала, 
– частота предмодального интервала, 
– частота постмодального интервала. Модальный интервал – интервал, имеющий максимальную частоту.
Медиана
Для дискретного вариационного ряда:
, если n нечетное, и 
, если n четное.
Для интервального вариационного ряда:
.
Здесь – нижняя граница медианного интервала, – длина медианного интервала, 
– объем выборки, 
– частота медианного интервала, 
– накопленная частота вплоть до предмедианного интервала (включительно). Медианный интервал – первый интервал, накопленная частота которого превышает половину объема выборки.
Медианный интервал можно найти по номеру медианной единицы ряда: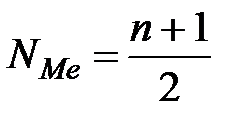 
. Первый интервал, накопленная частота которого больше или равна 
, является медианным интервалом.
Меры вариации (колеблемости)
Размах вариации
.
Формула Стерджесса для определения оптимального числа групп: 
.
Дисперсия и среднеквадратическое отклонение
Для несгруппированных данных:
; 
= 
;
Для сгруппированных данных:
; 
= 
;
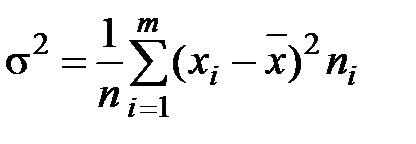Общая формула: 
,
где 
для несгруппированных данных,
или 
для сгруппированных данных.
Коэффициент вариации
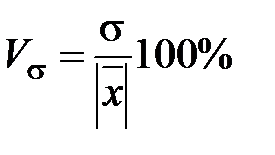
Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальным).
Среднее линейное отклонение
; (невзвешенное),
(взвешенное).
Между средним линейным и средним квадратическим отклонениями существует следующее примерное соотношение: 
, если фактическое распределение близко к нормальному.
Коэффициент осцилляции
Коэффициент линейной вариации
.
Доверительные интервалы
Средняя ошибка наблюдений количественного признака (средняя ошибка среднего значения):
(повторный отбор); 
(бесповторный отбор).
Предельная ошибка наблюдений количественного признака (предельная ошибка среднего значения):
(повторный отбор);
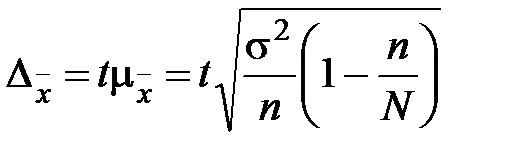(бесповторный отбор),
где t – коэффициент доверия.
Средняя ошибка наблюдений альтернативного признака (средняя ошибка доли):
(повторный отбор);
(бесповторный отбор).
Предельная ошибка наблюдений альтернативного признака (предельная ошибка доли)
(повторный отбор);
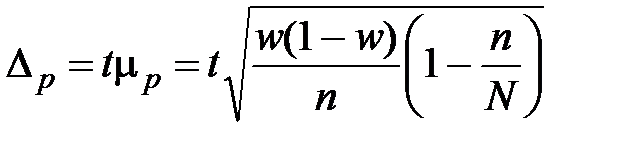(бесповторный отбор).
Здесь t – коэффициент доверия.
Если объем выборки 
, то его находят из таблиц функции Лапласа 
как корень уравнения 
, где γ – заданная доверительная вероятность (надежность): 
.
Доверительный интервал 
: 
Объем выборки, обеспечивающий заданную точность с заданной надежностью,
для среднего значения (количественного признака):
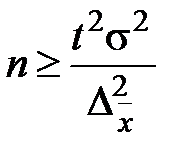(повторный отбор); 
(бесповторный отбор);
для доли (альтернативного признака):
(повторный отбор);
(бесповторный отбор).
Можно использовать максимальное значение дисперсии альтернативного признака:
(повторный отбор); 
(бесповторный отбор),
т. к. 
, поскольку 
.
Малая выборка
Выборка считается малой, если объем выборки 
.
Исправленная дисперсия 
Средняя ошибка наблюдений количественного признака (средняя ошибка среднего значения)
(повторный отбор);
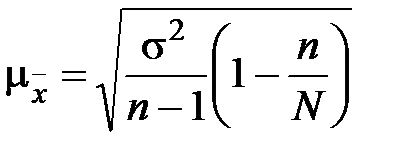(бесповторный отбор).
Средняя ошибка наблюдений альтернативного признака (средняя ошибка доли)
(повторный отбор);
(бесповторный отбор);
Предельная ошибка наблюдений количественного признака (предельная ошибка среднего значения):
(повторный отбор); 
(бесповторный отбор);
Предельная ошибка наблюдений альтернативного признака (предельная ошибка доли):
(повторный отбор);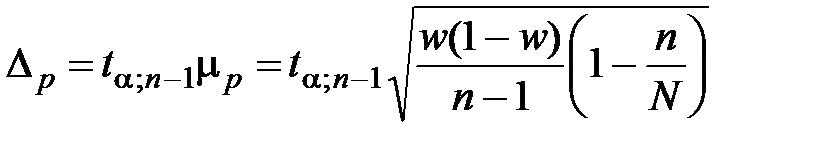 
(бесповторный отбор).
Здесь 
– коэффициент доверия для малой выборки. Его находят по таблицам критических точек распределения Стьюдента для двусторонней области при 
, где γ – доверительная вероятность (надежность). Если коэффициент доверия ищут по таблицам распределения Стьюдента для односторонней области, то вместо нужно брать 
. Этот же коэффициент можно найти по специальным таблицам для 
.
Объем выборки, обеспечивающий заданную точность с заданной надежностью,
для среднего значения (количественного признака):
(повторный отбор);
(бесповторный отбор);
для доли (альтернативного признака):
(повторный отбор);
(бесповторный отбор).
Если использовать максимальное значение дисперсии доли, то
(повторный отбор);
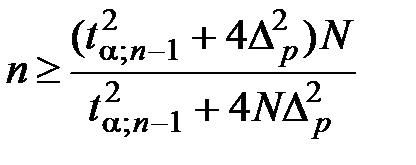(бесповторный отбор), т. к. .
Линейная регрессия.
Корреляционно-регрессионный анализ
Уравнение линейной регрессии: 
, где 
, 
.
Коэффициент корреляции Пирсона: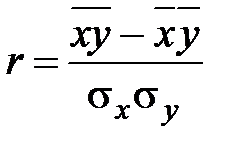 
; 
.
Коэффициент детерминации: 
,
где 
.
Коэффициент детерминации показывает величину вариации переменной y, которая объясняется переменной x, при наличии линейной связи этих величин. В случае строгой функциональной линейной зависимости между переменными x и y коэффициент детерминации 
. Если линейная зависимость между x и y отсутствует, то 
.
– это общая вариация переменной y.
– это вариация переменной y, которая объясняется формулой .
– это вариация переменной y, которая не объясняется формулой . Разница 
называется ошибкой (остатком, отклонением). Значения коэффициентов a и b в уравнении подбираются (методом наименьших квадратов) так, чтобы минимизировать сумму квадратов всех отклонений: 
.