.7.1 Для задачи решения в контрольном задании 2 потребуется знание теории в объёме:
Показатели 2рядов динамики Приемы выравнивания динамических рядов
2.7.2 Полезные вопросы для самопроверки:
1.Как называются элементы ряда динамики?
2.Какие показатели ряда динамики относятся к абсолютным. к относительным, к средним?
3. С какой целью производят выравнивание динамического ряда?
2.7.3 Решение типовой задачи 4
Типовая задача 4
По данным о выпуске продукции (таблица 8) провести аналитическое выравнивание по прямой.
Таблица 8 – Исходные данные
| Год | |||||||||
| Производство продукции млн.р. |
Методика выполнения типовой задачи 4
При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменение уровней ряда динамики могут быть с той или иной степенью приближения выражены определенным математическим законом. На основе теоретического анализа выявляется характер развития явления во времени и выбирается то или иное математическое выражение типа закономерности изменения явления: по прямой, параболе второго порядка, гиперболе и т. п.,
Для выравнивания ряда динамики по прямой, используют адекватную формулу:
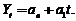
Параметры уравнения а 0 и a1 можно найти из системы уравнений


где у – исходные (эмпирические) уровни ряда динамики;
n – число уровней ряда динамики;
t – порядковый номер периода времени.
Для упрощения расчетов параметров адекватной формулы можно ввести такую нумерацию периодов времени, при которой  В этом случае:
В этом случае:


Для достижения  нумерация уровней ряда динамики проводится следующим образом:
нумерация уровней ряда динамики проводится следующим образом:
если ряд динамики состоит из нечетного числа уровней, то уровню, находящемуся в середине ряда присваивается порядковый номер «О», предыдущие уровни нумеруются по порядку • отрицательными числами, последующие -положительными, как это показано в таблице 9.
Если ряд динамики состоит из четного числа уровней, то двум уровням, находящимся посередине присваиваются номера -1 и +1, предыдущие уровни нумеруются отрицательными нечетными числами; последующие – положительными нечетными числами, например:
| январь | февраль | март | апрель | май | июнь | |
| № п/п | –5 | –3 | –1 | +1 | +3 | +5 |
Необходимые данные для нахождения параметров можно определить с помощью таблицы 9, где у – эмпирические уровни ряда, at – условное обозначения периода времени.
Таблица 9 – Расчетная таблица для определения параметров адекватной формулы развития ряда динамики
| Год | Эмпирические уровни ряда, у | Условное обозначение периода времени, / | t2 | 
| Yt |
| –4 | –884 | 219,32 | |||
| –3 | –705 | 241,24 | |||
| –2 | –544 | 263,16 | |||
| –1 | –285 | 285,08 | |||
| 307,00 | |||||
| 328,92 | |||||
| 350,84 | |||||
| 372,76 | |||||
| 394,68 | |||||
| Итого | 2763,00 |

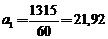 .
.
В результате получаем следующее уравнение общей тенденции ряда динамики:
Yt = 307+21,92*t.
Подставляя в уравнение Yt = 307+2l,92*t принятые обозначения t, вычислим выравненные (теоретические) уровни ряда динамики например:
для 1 гогода: Yt = 307+21,92(- 4)  219,32
219,32
для 2 гогода: Yt = 307+21,92(- 3)  241,24 и т. д.
241,24 и т. д.
Контрольное задание 4
Произвести выравнивание ряда динамики по прямой (в соответствии с заданным вариантом).
Таблица 10 – Варианты исходных данных
| Месяц | Месячная выплавка чугуна, тыс. т. | Основные фонды, млн. р. | Потребление электроэнергии млрд. кВт, ч. | Розничный товарооборот области, млрд. р. | Число родившихся, тыс. чел. |
| Вариант | |||||
| Январь | 10,1 | 27,0 | 26,0 | 7,4 | |
| февраль | 10,5 | 29,2 | 26,1 | 7,9 | |
| Март | 11,0 | 30,0 | 27,1 | 8,7 | |
| Апрель | 10,6 | 35,0 | 28,7 | 8,2 | |
| Май | 12,1 | 37,0 | 30,6 | 7,9 | |
| Июнь | 12,8 | 38,0 | 32,4 | 8,2 | |
| Июль | 13,2 | 37,3 | 34,4 | 8,8 | |
| Август | 13,6 | 39,4 | 36,3 | 8,7 | |
| Сентябрь | 14,1 | 39,8 | 38,0 | 8,7 | |
| Октябрь | 14,3 | 41,2 | 40,2 | 8,9 | |
| Ноябрь | 14,7 | 40,9 | 42,1 | 9,1 | |
| Декабрь | 15,2 | 43,0 | 44,1 | 9,3 |
Таблица11– Варианты исходных данных
| Месяц | Месячная выплавка чугуна, тыс. т. | Основные фонды, млн. р. | Потребление электроэнергии млрд. кВт, ч. | Розничный товарооборот области, млрд. р. | Число родившихся, тыс. чел. |
| Вариант | |||||
| Январь | 10,1 | 27,0 | 26,0 | 7,4 | |
| февраль | 10,5 | 29,2 | 26,1 | 7,9 | |
| Март | 11,0 | 30,0 | 27,1 | 8,7 | |
| Апрель | 10,6 | 35,0 | 28,7 | 8,2 | |
| Май | 12,1 | 37,0 | 30,6 | 7,9 | |
| Июнь | 12,8 | 38,0 | 32,4 | 8,2 | |
| Июль | 13,2 | 37,3 | 34,4 | 8,8 | |
| Август | 13,6 | 39,4 | 36,3 | 8,7 | |
| Сентябрь | 14,1 | 39,8 | 38,0 | 8,7 | |
| Октябрь | 14,3 | 41,2 | 40,2 | 8,9 | |
| Ноябрь | 14,7 | 40,9 | 42,1 | 9,1 | |
| Декабрь | 15,2 | 43,0 | 44,1 | 9,3 |