2..7.1 Для решения задачи в контрольном задании5 потребуется знание теории в объёме:
Способы отбора при выборочном наблюдении. Определение необходимой численности выборки. Ошибки выборочного наблюдения.
2.7.2 Полезные вопросы для самопроверки:
:
1. Дайте понятие ошибкам репрезентативности.
2. Дайте характеристику факторам, определяющим среднюю и предельную ошибки выборки?
2.7.3Решение типовой задачи 5
Типовая задача 5
Методом случайной повторной выборки было взято для проверки на вес 200 шт. деталей. В результате проверки был установлен средний вес детали (ЗОг) при среднем квадратическом отклонении 4 г. С вероятностью 0,954 требуется определить предел, в котором находится средний вес деталей в генеральной совокупности.
Методика выполнения типовой задачи 5
Надежность результатов выборки проверяется расчетами ошибок: средней ошибки выборки и предельной ошибки выборки.
Средняя ошибка (ц) зависит от способа отбора (повторного или бесповоротного) и рассчитывается:
при бесповторном отборе
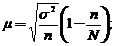
при повторном отборе

где n - численность выборки;
N - численность генеральной совокупности;
 – дисперсия выборочной совокупности. Предельная ошибка выборки (
– дисперсия выборочной совокупности. Предельная ошибка выборки ( ) рассчитывается по формуле
) рассчитывается по формуле

где t - коэффициент доверия, зависит от значения вероятности [F (t) ] при F(t) = 0,997 t = 3; при F(t) - 0,988 t - 2,5; при F(t) = 0,954 t = 2; при F(t) = 0,866 t = 1,5; при F(t) = 0,683 t = /; при F(t) = 0,383 t = 0,5.
В типовой задаче задано  - 4, следовательно,
- 4, следовательно,  = 16. Тогда
= 16. Тогда
при повторном отборе 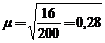 (г):
(г):
Предельная ошибка выборочной средней с вероятностью F(t)= 0,954
t = 2 составит  = 2*0,28 = 0,56 (г)
= 2*0,28 = 0,56 (г)
Верхняя граница среднего веса в генеральной совокупности будет равна
30 + 0,56 = 30,56
Нижняя граница 30 - 0,56 = 29,44 (г).
С вероятностью 0,954 можно утверждать, что средний вес детали колеблется в пределах
29,44 
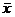
 30,56.
30,56.
Контрольное задание 5
Вариант 1
Для определения средней длины деталей необходимо провести выборочное обследование методом случайного повторного отбора. Какое количество деталей нужно отобрать, чтобы ошибка выборки не превышала 2 мм с вероятностью 0,954 при квадратическом отклонении 8 мм?
Вариант 2
В порядке случайного бесповоротного контроля веса изделий были получены: величина дисперсии признака, равная 20 г, и средний вес изделия, равный 16 г. Определить вероятность того, что средняя по всей партии изделий отличается от выборочной средней не более чем на 0,5 г. Вся партия изделий равна 10000 шт., контролю подвергнуто 500 шт.
Вариант 3
При определении средней продолжительности поездки на работу проводится 10 % выборка работающего населения. Численность работающего населения города - 17400 чел. Средняя продолжительность поездки - 43 минуты, при среднем квадратическом отклонении 16 минут. Определить с вероятностью 0,997 среднюю продолжительность поездки работающего населения города.
Вариант 4
Для определения зольности угля месторождения в порядке случайной повторной выборки взято 370 проб. В результате лабораторных исследований установлена средняя зольность угля в выборке 17 % с дисперсией выборки 6 %. С вероятностью 0,997 определить пределы, в которых находится средняя зольность угля месторождения.
Вариант 5
Какое число студентов нужно отобрать в порядке бесповторного случайного отбора для определения их среднего возраста из 4000 студентов высшего учебного заведения, чтобы предельная ошибка с вероятностью 0,954 не превышала 0,5 года. Известно, что среднее квадратическое отклонение возраста студента составляет 1,5 года
Вариант 6
Для определения средней длины деталей необходимо провести выборочное обследование методом случайного повторного отбора. Какое количество деталей нужно отобрать, чтобы ошибка выборки не превышала3мм с вероятностью 0,997 при квадратическом отклонении9 мм?
Вариант 7
В порядке случайного бесповоротного контроля веса изделий были получены: величина дисперсии признака, равная 30 г, и средний вес изделия, равный 15 г. Определить вероятность того, что средняя по всей партии изделий отличается от выборочной средней не более чем на 0,7 г. Вся партия изделий равна 10000 шт., контролю подвергнуто 400 шт.
Вариант 8
При определении средней продолжительности поездки на работу проводится 15 % выборка работающего населения. Численность работающего населения города - 25000 чел. Средняя продолжительность поездки - 23 минуты, при среднем квадратическом отклонении 17 минут. Определить с вероятностью 0,995 среднюю продолжительность поездки работающего населения города.
Вариант 9
Для определения зольности угля месторождения в порядке случайной повторной выборки взято 150 проб. В результате лабораторных исследований установлена средняя зольность угля в выборке 20 % с дисперсией выборки 9 %. С вероятностью 0,997 определить пределы, в которых находится средняя зольность угля месторождения.
Вариант 10
Какое число студентов нужно отобрать в порядке бесповторного случайного отбора для определения их среднего возраста из 6000 студентов высшего учебного заведения, чтобы предельная ошибка с вероятностью 0,954 не превышала 0,5 года. Известно, что среднее квадратическое отклонение возраста студента составляет 1,3года.
3. Контрольные вопросы по курсу для подготовки к экзамену, зачёту
1. Предмет и метод статистики. Основные задачи статистической науки.
2. История возникновения и развития статистики.
3. Отрасли статистической науки. Связь статистики с другими дисциплинами.
4. Организация статистики в Российской Федерации.
5. Организация статистики за рубежом. Международные статистические организации.
6. Статистическое наблюдение - первый этап статистического исследования.
7. Виды, формы и способы статистического наблюдения.
8. Программно-методологические вопросы статистического наблюдения.
9. 0рганизационный план статистического наблюдения.
10. Программа и инструментарий статистического наблюдения.
11. Статистическая отчетность – ведущая форма статистического наблюдения.
12. Ошибки и контроль данных статистического наблюдения.
13. Понятие статистической сводки. Виды сводок и этапы сводок.
14. Понятие о группировке и группировочном признаке.
15. Виды статистических группировок.
16. Номенклатура и важнейшие классификации, применяемые в статистике.
17. Статистические таблицы и правила их построен я.
18. Графическое изображение статистических данных. Элементы статистического графика.
19. Виды статистических графиков и правила их построения.
20. Понятие о статистическом показателе, его значение и функции.
21. Виды и основные показатели абсолютных величин.
22. Виды и основные показатели относительных величин.
23. Понятие о средних. Основные положения теории средних величин.
24. Средняя арифметическая и ее свойства.
25. Различные виды средних величин.
26. Структурные средние - мода и медиана.
27. Понятие о вариации. Основные показатели вариации.
28. Дисперсия и ее свойства. Правило сложения дисперсий.
29. Дисперсия альтернативного признака.
30. Понятие о выборочном наблюдении. Генеральная и выборочная совокупность, генеральная и выборочная средняя
31. Виды и способы отбора. Повторная и бесповторная схемы отбора.
32. Определение средних и предельных ошибок выборки.
33. Определение необходимой численности выборки
34. Практика применения выборочного наблюдения;.
35. Понятие о рядах динамики. Классификация динамических рядов.
36. Основные показатели рядов динамики.
37. Приемы обработки и анализа динамических рядов.
38. Способ скользящей средней. Аналитическое выравнивание по прямой.
39. Виды и формы связи между явлениями. Функциональные и корреляционные виды связи.
40. Определение тесноты связи между явлениями. Отбор факторных признаков.
41. Линейный коэффициент корреляции, коэффициент детерминации.
42. Множественная корреляция.
43. Понятие об индексах. Задачи, решаемые при помощи индексов. Индивидуальные и общие индексы.
44. Базисные и цепные индексы.
46. Агрегатная форма построения индексов. Правило индексирования.
47.Среднеарифметический и среднегармонический индексы.
48. Индексы переменного и постоянного (фиксированного) состава.
49. Система взаимосвязанных индексов.
50. Индексный метод определения влияния отдельных факторов на общий результат.