Задания для домашней контрольной работы и методические рекомендации по её выполнению

Контрольная работа предусмотрена учебным планом заочного отделения и составлена по вариантам индивидуально для каждого учащегося.

Номера задач, которые учащийся решает в контрольной работе, даны в таблице 2. Вариант контрольной работы определяется двумя последними цифрами личного номера учащегося.

Каждый вариант контрольной работы включает 5 задач.

Ответы на теоретические вопросы учащийся должен изложить своими словами. Рисунки, электрические схемы и векторные диаграммы выполняют простым карандашом.

Задача №1 выполняется послесамостоятельного изучения темы 1.2. «Электрические цепипостоянного тока».

Задачу №2 выполняется после самостоятельного изучения темы 1.5. «Однофазныеэлектрические цепи переменного тока».

Задачу № 3 выполняют после самостоятельного изучения темы 1.6. «Трехфазные электрические цепи».

Задача № 4 выполняется после самостоятельного изучения темы 1.8. «Электрические машины переменного тока».

Задача № 5 выполняется после самостоятельного изучения тем 2.2. «Полупроводниковые приборы» и 2.4. «Электронные выпрямители и стабилизаторы».

При выполнении домашней контрольной работы необходимо соблюдать следующие требования:

 

Таблица 2

Номера	Номера	Номера	Номера
Вариантов	Задач	Вариантов	Задач	Вариантов	Задач	Вариантов	Задач
1.	1; 2; 3;	26.	1; 2; 3;	51.	1; 2; 4;	76.	1; 2; 5;
2.	1; 2; 3;	27.	1; 2; 3;	52.	1; 2; 4;	77.	1; 2; 5;
3.	1; 2; 3;	28.	1; 2; 3;	53.	1; 2; 4;	78.	1; 2; 5;
4.	1; 2; 3;	29.	1; 2; 3;	54.	1; 2; 4;	79.	1; 2; 5;
5.	1; 2; 3;	30.	1; 2; 3;	55.	1; 2; 4;	80.	1; 2; 5;
6.	1; 2; 3;	31.	1; 2; 3;	56.	1; 2; 4;	81.	1; 2; 6;
7.	1; 2; 3;	32.	1; 2; 3;	57.	1; 2; 4;	82.	1; 2; 6;
8.	1; 2; 3;	33.	1; 2; 3;	58.	1; 2; 4;	83.	1; 2; 6;
9.	1; 2; 3;	34.	1; 2; 3;	59.	1; 2; 4;	84.	1; 2; 6;
10.	1; 2; 3;	35.	1; 2; 3;	60.	1; 2; 4;	85.	1; 2; 6;
11.	1; 2; 3;	36.	1; 2; 3;	61.	1; 2; 5;	86.	1; 2; 6;
12.	1; 2; 3;	37.	1; 2; 3;	62.	1; 2; 5;	87.	1; 2; 6;
13.	1; 2; 3;	38.	1; 2; 3;	63.	1; 2; 5;	88.	1; 2; 6;
14.	1; 2; 3;	39.	1; 2; 3;	64.	1; 2; 5;	89.	1; 2; 6;
15.	1; 2; 3;	40.	1; 2; 3;	65.	1; 2; 5;	90.	1; 2; 6;
16.	1; 2; 3;	41.	1; 2; 3;	66.	1; 2; 5;	91.	1; 2; 7;
17.	1; 2; 3;	42.	1; 2; 3;	67.	1; 2; 5;	92.	1; 2; 7;
18.	1; 2; 3;	43.	1; 2; 3;	68.	1; 2; 5;	93.	1; 2; 7;
19.	1; 2; 3;	44.	1; 2; 3;	69.	1; 2; 5;	94.	1; 2; 7;
20.	1; 2; 3;	45.	1; 2; 3;	70.	1; 2; 5;	95.	1; 2; 7;
21.	1; 2; 3;	46.	1; 2; 3;	71.	1; 2; 5;	96.	1; 2; 7;
22.	1; 2; 3;	47.	1; 2; 3;	72.	1; 2; 5;	97.	1; 2; 7;
23.	1; 2; 3;	48.	1; 2; 3;	73.	1; 2; 5;	98.	1; 2; 7;
24.	1; 2; 3;	49.	1; 2; 3;	74.	1; 2; 5;	99.	1; 2; 7;
25.	1; 2; 3;	50.	1; 2; 3;	75.	1; 2; 5;	100.	1; 2; 7;

 

Методические указания к решению задачи 1

Решение задачи требует знаний закона Ома для всей цепи и ее участков, законов Кирхгофа, методики определения эквивалентного сопротивления цепи при смешанном соединении резисторов, а также умения вычислять мощность и работу электрического тока. Содержа­ния задач и схемы цепей приведены в условии, а данные к ним — в таблице 1. Перед решением задачи рассмотрите типовой пример 1.

Пример 1. Для схемы, приведенной на рис. 1, а, определить экви­валентное сопротивление цепи R_АВ и токи в каждом резисторе, а также расход электроэнергии цепью за 8 ч работы.

Решение. Задача относится к теме «Электрические цепи по­стоянного тока». Проводим поэтапное решение, предварительно обозна­чив стрелкой ток в каждом резисторе; индекс тока должен соответство­вать номеру резистора, по которому он проходит.

1. Определяем общее сопротивление разветвления R_CD, учитывая, что резисторы R₃ и R₄ соединены последовательно между собой, а с резистором R₅ параллельно:

2. Определяем общее сопротивление цепи относительно вводов СЕ. Резисторы и R_CD и R₂ включены параллельно, поэтому

3. Находим эквивалентное сопротивление всей цепи: R_АВ = R₁ + R_СЕ = 8 + 2 = 10 Ом (рис. 1, г).

4. Определяем токи в резисторах цепи. Так как напряжение U_AB приложено ко всей цепи, а R_АВ = 10 Ом, то согласно закону Ома I₁ =U_AB/ R_AB = 150/10 = 15 А.

Внимание! Нельзя последнюю формулу писать в виде I₁ = U_AB / R₁, так как U_АВ приложено ко всей цепи, а не к участку R₁.

Для определения тока I₁ находим напряжение на резисторе R₂, т. е. U_CE. Очевидно, U_CB меньше U_AB на потерю напряжения в ре­зисторе R₁, т. е. U_СЕ = U_АВ – I₁R₁ = 150 – 15_*8 = 30 В. Тогда I₁ = U_CE/ R₂ = 30/3 = 10 А. Так как U_CD= U_CD, то можно определить токи I_3,4 и I₅: I_3,4 = U_CD/(R₃ + R₄) = 30/(10 + 5) = 2 А; I₅ = U_CD/R₅ = 30/10 = 3 А.

На основании первого закона Кирхгофа, записанного для узла С, проверим правильность определения токов:

I₁ = I₂ + I₃,₄ + I₅, или 15 = 10 + 2 + 3 = 15 А.

5. Расход энергии цепью за восемь часов работы:

W = Pt = U_ABI₁t = 150·15·8 = 18 000 Вт·ч = 18 кВт·ч.

Пусть в схеме примера 1 известны сопротивления всех резисторов, а вместо напряжения U_AB задан один из токов, например I₂ = 2 А. Найти остальные токи и напряжение U_AB. Зная I₂, определяем U_CE = I₂R₂ = 2-3 = 6 В. Так как U_CE = U_CD, то

I_3,4 = U_CD/(R₃ + R₄) = 6/(10 + 5) = 0,4 А;

I₅= U_CD / R₅ = 6/10 = 0,6 А.

На основании первого закона Кирхгофа I₁ = I₂ + I_3,4 + I₅ = 2 + 0,4 + 0,6 =3А. Тогда U_AB = U_CE + I₁R₁ = 6 + 3·8 = 30 В.

При расплавлении предохранителя Пр₅ резистор R₅выключается и схема принимает вид, показанный на рис. 1, д. Вычисляем экви­валентное сопротивление схемы: R'_AB = R₁+ (R₃ + R₄)·R₂ / (R₃+R₄R₂) = 8 + (10 + 5)·3 / (10 + 5 + 3) = 10,5 Ом. Так как напряжение U_AB остается неизменным, находим ток I₁ = U_AB/R'_AB = 150/10,5 = 14,28 А. Напряжение U_CE = U_AB – I₁R₁ = 150 - 14,28·8 =35,75 В.

Тогда токи

I₂ = U_CE/R₂ = 35,75/3 = 11,9 A; I_3,4 = U_CE/R_3,4 = 35,75/(10 + 5) = 2,38 A.

Сумма этих токов равна току I₁: 11,9 + 2,38 = 14,28 А.

Рис.1

Методические указания к решению задачи 2

Эта задача относится к неразветвленным и разветвленным цепям переменного тока. Перед ее решением изучите материал темы 1.5, ознакомьтесь с методикой построения векторных диаграмм, изложенной ранее.

Пример 2. Неразветвленная цепь переменного тока содержит катушку с активным, сопротивлением R_K=3 Ом и индуктивным X_L=12 Ом, активное сопротивление R=5 Ом и конденсатор с сопротивлением X_C = 6 Ом (рис. 2,а). К цепи приложено напряжение U=100В (действующее значение).

Определить: 1) полное сопротивление цепи; 2) ток; 3) коэффициент мощности; 4) активную, реактивную и полную мощности; 5) напряжение на каждом сопротивлении. Начертить в масштабе векторную диаграмму цепи.

Решение. 1. Определяем полное сопротивление цепи:

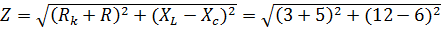= 10 Ом.

2. Определяем ток цепи: I = U/Z = 100/10 = 10 А.

3. Находим коэффициент мощности цепи. Во избежание потери знака угла (косинус - функция четная) определяем sin φ: sin φ=(X_L–X_C)/Z = (12–6)/10 = 0,6; φ = 36°50'. По таблицам Брадиса определяем коэффициент мощности cos φ = cos 36°50' = 0,8.

4. Определяем активную, реактивную и полную мощности цепи:

Р = U·I·cosφ = 100·10·0,8 = 800 ВтилиР = I²·(R_K+R)=10²·(3+5) =800 Вт;

Q = I²·(X_L–X_C) = 10²·(12 – 6) =600 варили Q=U· I ·sinφ=1000·10·0,6=600 вар;

илиS=U·I=100·10=1000 B·АилиS=I²·Z=10²·10=1000 В·А

5. Определяем падения напряжения на сопротивлениях цепи: U_L=10·3=30 В; U_L=I·X_L=10·12=120 В; U_R=I·R=10·5=50 В; U_C=I·Х_C=10·6 = 60 В.

Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: в 1 см - 2,0 А и масштабом по напряжению: в 1 см - 20 В. Построение векторной диаграммы (рис. 2, б) начинаем с вектора тока, который откладываем по горизонтали в масштабе 10 А/2 А/см = 5 см.

Рис. 2

Вдоль вектора тока откладываем векторы падений напряжения на активных сопротивлениях U_RK и U_R: 30 В/20 В/см = 1,5 см; 50 В/20 В/см = 2,5 см.

Из конца вектора U_R откладываем в сторону опережения вектора тока на 90° вектор падения напряжения U_L на индуктивном сопротивлении длиной 120 В/20 В/см = 6 см. Из конца вектора U_L откладываем в сторону отставания от вектора тока на 90° вектор падения напряжения на конденсаторе Uc длиной 60 В/20 В/см = 3 см. Геометрическая сумма векторов U_RK, U_R, U_L, U_Cравна полному напряжению, приложенному к цепи.

 

Методические указания к решению задачи 3

Решение задач этой группы требует знания учебного материала темы 1.6, представления об особенностях соединения источников и по­требителей в звезду и треугольник, соотношениях между линейными и фазными напряжениями и токами при таких соединениях, умения строить векторные диаграммы при симметричной и несимметричной нагрузках, а также в аварийных режимах. Для пояснения методики решения задач на трехфазные цепи приведены примеры 3—4 с подробными решениями.

Пример 3. В четырехпроводную сеть включена несимметричная нагрузка, соединенная в звезду (рис. 3, а). Линейное напряжение сети U_ном = 380 В. Определить токи в фазах и начертить векторную диаграмму цепи внормальном режиме и при отключении автомата влинейном проводе А. Из векторных диаграмм графически найти ток нулевом проводе в обоихслучаях.

Решение. Определяем:

1. Фазное напряжение

2. Токи в фазах:

3. Углы сдвига фаз в каждой фазе:

 

 

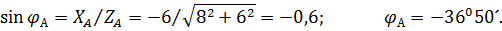
так как в фазе С есть только активное сопротивление.

4. Для построения векторной диаграммы выбираем масштабы по току:

1 см — 10 А и напряжению: 1 см — 40 В. Построение диаграммы начинаем с векторов фазных напряжений U_А, U_В, U_С (рис. 3,б), располагая их под углом 120° друг относительно друга. Чередование фаз обычное: за фазой А — фаза В, за фазой В — фаза С.

Рис.3

В фазе А угол сдвига φ_Aотрицательный, т. е. ток I_A опережает фазное напряжение U_A на угол φ_A= — 36°50´. Длина вектора тока I_A в принятом масштабе составит 22/10=2,2 см, а длина вектора фазного напряжения U_A — 220/40 = 5,5 см.

В фазе В угол сдвига φ_B> 0, т. е. ток отстает от фазного напряжения U_B на угол φ_B= 53° 10'; длина вектора тока I_B равна 44/10= 4,4 см.

В фазе С ток и напряжение Uc совпадают по фазе, так как φ_C= 0. Длина вектора тока I_C составляет 22/10 = 2,2 см.

Ток в нулевом проводе I₀ равен геометрической сумме трех фазных токов. Измеряя длину вектора тока I₀, получаем в нормальном режиме 4,5 см, поэтому I₀ = 45 А. Векторы линейных напряжений на диаграмме непоказаны, чтобы не усложнять чертеж.

5. При отключении линейного автомата в фазе А на векторной диаграмме

остаются фазные напряжения U_В и U_С и продолжают протекать в этих фазах токи I_B и I_C. Ток I_А=0. Поэтому ток в нулевом проводе равен геометрической сумме токов фаз В и С (рис. 3,б). Измеряя длину вектора тока , получаем 5,5 см, или 55 А.

Пример 4. В трехфазную сеть включили треугольником несимметричную нагрузку (рис. 4, а): в фазу АВ — активное сопротивление R_AB = 10 Ом; в фазу ВС — индуктивное сопротивление Х_BC = 6 Ом и активное R_BC = 8 Ом; в фазу СА — активное сопротивление R_CA = 5 Ом. Линейное напряжение сети U_ном=220 В. Определить фазные токи и начертить векторную диаграмму цепи, из которой графически найти линейные токи в следующих случаях: 1) в нормальном режиме; 2) при аварийном отключении линейного провода А; 3) при аварийном отключении фазы АВ.

Решение. 1. Нормальный режим. Определяем фазные токи:

 

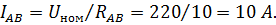
Вычисляем углы сдвига фаз в каждой фазе: 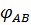=0; . =0;

Для построения векторной диаграммы выбираем масштаб по току: см — 10 А и напряжению: 1 см — 40 В. Затем в принятом масштабе откладываем векторы фазных (они же линейные) напряжений U_AB,U_DC, U_СА под углом друг относительно друга (рис. 4,б).

Затем откладываем векторы фазных токов: ток в фазе АВ совпадает с напряжением U_AB; в фазе ВС ток отстает от напряжения U_ВС на угол φ_ВС= 36°50'; ток в фазе СА совпадает с напряжением U_СА. Затем строим векторы линейных токов на основании известных уравнений: 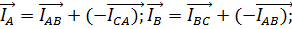Измеряя длины векторов линейных токов и пользуясь масштабом, находим их значение:I_А = 55 А; I_В = 43 А; I_С = 48 А.

 

Рис.4

2. Аварийное отключение линейного провода А. В этом случае трехфазная цепь превращается в однофазную с двумя параллельно включенными ветвями САВ и ВС и рассчитывается обычная однофазная схема с одним напряжением Uвс. Определи токи I_САВ и I_ВС.Неполное сопротивление ветви Z_CAB= R_CA + R_AB = 5+10= 15 Ом. Сила тока I_CAB= U_BC/Z_CAB= 220/15 = 14,7 А; φ_САВ= 0.

Полное сопротивление ветви ВС Сила тока I_ВС= 220/10 = 22 А; φ_ВС = 36°50'. На рис. 4, в построена векторная диаграмма цепи. Из диаграммы находим линейные токи: I_В = I_С= 38 А. По направлению же эти токи обратны.

3. Аварийное отключение фазы АВ. При этом ток отключенной фазе равен нулю, а токи в двух других фазах остаются прежними. На рис. 4, г показана векторная диаграмма для этого случая. Ток I_АВ= 0; линейные токи определяются согласно уравнениям:

Таким образом, только линейный ток I_С сохраняет своювеличину; токи I_А и I_В изменяются до фазных значений. Из диаграммы графически находим линейные токи: I_А = 44 А; I_В = 22 А; I_С = 45 А.

 

Методические указания к решению задачи 4

Задачи этой группы относятся к теме «Электрические машины переменного тока». Для их решения необходимо знать устройство и принцип действия асинхронного двигателя с короткозамкнутым и фазным ротором и зависимости между электрическими величинами, характеризующими его работу. Особое внимание уделите § 8.1—8.14 учебника. Необходимо ознакомиться с рядом возможных синхронных частот вращения магнитного потока при частоте тока 50 Гц: 3000, 1500, 1000, 750, 600 об/мин и т.д. Поэтому при частоте вращения ротора, например, n₂= 980 об/мин поле может иметь только n₁ = 1000 об/мин (ближайшая к 980 об/мин из ряда синхронных частот вращения) и можно сразу определить скольжение, даже не зная числа пар полюсов: s = (n₁— n₂)/n₁= (1000— 980)/1000 = 0,02.

В настоящее время промышленность выпускает асинхронные двигатели серии 4А мощностью от 0,06 до 400 кВт (табл. 3). Обозначение типа двигателя расшифровывается так: А — асинхронный; 4 — номер серии; X — алюминиевая оболочка и чугунные щиты (отсутствие буквы X означает, что корпус полностью выполнен из чугуна); В — двигатель встроен в оборудование; Н — исполнение защищенное IP23; для закрытых двигателей исполнения IP44 буквы Н нет; Р — двигатель с повышенным пусковым моментом; С — сельскохозяйственного назначения; цифра после буквенного обозначения показывает высоту оси вращения в мм; буквы S, М, L после цифр дают установочные размеры по длине корпуса (S — самая короткая станина; М — промежуточная; L — самая длинная); цифра после установочного размера — число полюсов; У — климатическое исполнение (для умеренного климата); последняя цифра показывает категорию размещения (1 — для работы на открытом воздухе, 3 — для закрытых неотапливаемых помещений). В обозначении типов двухскоростных двигателей после установленного размера указывают через дробь оба числа полюсов, например 4А160М8/4УЗ. Здесь 8 и 4 означают, что обмотки статора могут переключаться так, что в двигателе образуются 8 и 4 полюса.

Пример 5. Расшифровать условное обозначение двигателя АР180М4УЗ. Это двигатель четвертой серии, асинхронный, с повышенным пусковым моментом, корпус полностью чугунный (нет буквы X), высота оси вращения 180 мм; размеры корпуса по длине М (промежуточный), четырехполюсный для умеренного климата, третья категория размещения.

Пример 6. Трехфазный асинхронный двигатель с короткозамкнутым ротором типа 4А250S4У3 имеет номинальные данные (табл. 3): мощность Р_ном=75 кВт, напряжение U_ном=380 В; частота вращенияротора n₂= 1480 об/мин; КПД η_ном= 0,93; коэффициент мощности =0,87; кратность пускового тока 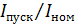=7,5; кратность пускового момента =1,2; способность к перегрузке = 2,2. Частота тока в сети =50Гц. Определить: 1) потребляемую мощность; 2) номинальный, пусковой и максимальный моменты; 3) номинальный и пусковой токи; 4) номинальное скольжение; 5) суммарные потери в двигателе; б) частоту тока в роторе.

Решение. 1. Мощность, потребляемая из сети,

= 75/0,93= 80,6 кВт.

 

 

Таблица 3

Тип двигателя	Рном, кВт	n2, об/мин					ηном
4A100S2У3			0,89	7,5	2,0	2,2	0,86
4A100L2У3	5,5		0,91	7,5	2,0	2,2	0,87
4А112М2СУ3	7,5		0,88	7,5	2,0	2,2	0,87
4А132М2СУ3			0,9	7,5	1,6	2,2	0,88
4А80А4У3	1,1		0,81	5,0	2,0	2,2	0,85
4А90 L4У3	2,2		0,83	6,0	2,0	2,2	0,8
4A100S4У3			0,83	6,5	2,0	2,2	0,82
4A100L4У3			0,84	6,5	2,0	2,2	0,84
4А112М4СУ1	5,5		0,85	7,0	2,0	2,2	0,85
4А132М4СУ1			0,87	7,5	2,0	2,2	0,87
4AP160S4У3			0,83	7,5	2,0	2,2	0,865
4АР160М4У3	18,5		0,87	7,5	2,0	2,2	0,885
4AP180S4У3			0,87	7,5	2,0	2,2	0,89
4 AP180М4У3			0,87	7,5	2,0	2,2	0,9
4А250S4У3			0,9	7.5	1,2	2,2	0,93
4А250М4У3			0,91	7,5	1,2	2,2	0,93
4А100L6У3	2,2		0,73	5,5	2,0	2,0	0,81
4АР160S6У3			0,83	7,0	2,0	2,2	0,855
4АР160М6У3			0,83	7,0	2,0	2,2	0,875
4АР180М6У3	18,5		0,8	6,5	2,0	2,2	0,87
4A250S6У3			0,89	6,5	1,2	2,2	0,92
4А250М6У3			0,89	7,0	1,2	2,0	0,92
4АН250М6У3			0,87	7,5	1,2	2,5	0,93
4A100L8У3	1,5		0,65	6,5	1,6	1,7	0,74
4 АР160S8У3	7,5		0,75	6,5	1,8	2,2	0,86
4А25058У3			0,83	6,0	1,2	1,7	0,9
4А250М8У3			0,84	6,0	1,2	1,7	0,91
4АН250М8У3			0,82	6,0	1,2	2,0	0,92
4A160S4/2У3
4А180S4/2У3
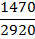
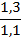
4А160М8/4У3
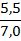
4А160S8/4У3

 

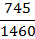
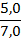
2. Номинальный момент, развиваемый двигателем,

М_ном = 9550Р_ном/n₂ = 9550 · 75/1480 = 484 Н·м.

3. Пусковой и максимальный моменты:

M_пуск = 1,2·М_ном= 1,2·484 = 581 Н·м;

М_max = 2,2·484 = 1064,8 Н·м.

4. Номинальный и пусковой токи:

I_пуск=7,5·I_ном=7,5·141=1057,5 А.

5. Номинальное скольжение

6. Суммарные потери в двигателе

7. Частота тока в роторе

Пример 7. Трехфазный асинхронный двигатель с фазным ротором имеет следующие данные: активное сопротивление фазы ротора R₂ = 0,25 Ом; индуктивное сопротивление фазы неподвижного ротора Х₂ =2,5 Ом. При вращении ротора с частотой n₂=1450 об/мин в фазе ротора наводится ЭДС E_2s=15 В. Определить: 1) ЭДС в фазе неподвижного ротора E₂; 2) ток в фазе ротора при нормальной работе I₂ и при пуске I_2пуск.

Решение. 1. Определяем скольжение ротора

s = (n₁ n₂)/n₁=(1500—1450)/ 1500 = 0,033.

2. ЭДС в фазе неподвижного ротора находим из формулы E_2s = E₂·s, откуда

E₂= E_2s/s= 15/0,033 = 454,5 В.

3. Ток в фазе ротора при пуске

4. Индуктивное сопротивление фазы ротора при s=0,033

x_2s= x₂·s = 2.5·0.033 = 0.08 Ом.

5. Ток в фазе вращающегося ротора

 

Методические указания к решению задачи 5

Задача 5 относится к расчету выпрямителей переменного тока, собранных на полупроводниковых диодах. Подобные схемы широко применяются в различных электронных устройствах и приборах. При решении задач следует помнить, что основными параметрами полупроводниковых диодов являются допустимый ток I_доп, на который рассчитан данный диод, и обратное напряжение U_обр, выдерживаемое диодом без пробоя в непроводящий период. Параметры диодов показаны в таблице 4.

Обычно при составлении реальной схемы выпрямителя задаютсязначением мощности потребителя Р_О, Вт, получающего питание от данного выпрямителя, и выпрямленным напряжением Uо, В, при котором работает потребитель постоянного тока. Отсюда нетрудно определить ток потребителя I_О=P_О/U_О. Сравнивая ток потребителя с допустимым током диода I_доп, выбирают диоды для схем выпрямителя.

Следует учесть, что для однополупериодного выпрямителя ток через диод равен току потребителя, т. е. надо соблюдать условие Iдоп ≥ Iо.

Для двухполупериодной и мостовой схем выпрямления ток через диод равен половине тока потребителя, т. е. следует соблюдать условиеI_доп≥0,5·Iо.

Для трехфазного выпрямителя ток через диод составляеттреть тока потребителя, следовательно, необходимо, чтобы I_доп ≥ I₀.

Таблица 4

Типы диодов			Типы диодов			Типы диодов
Д7Г	0,3		Д221	0,4		Д242
Д205	0,4		Д222	0,4		Д242А
Д207	0,1		Д224			Д242Б
Д209	0,1		Д224А			Д243
Д210	0,1		Д224Б			Д243А
Д211	0,1		Д226	0,3		Д243Б
Д214			Д226А	0,3		Д244
Д214А			Д231			Д244А
Д214Б			Д231Б			Д244Б
Д215			Д232			Д302
Д215А			Д232Б			Д303
Д215Б			Д233			Д304
Д217	0,1		Д233Б			Д305
Д218	0,1		Д234Б			КД202А
						КД202Н

Напряжение, действующее на диод в непроводящий период U_b, также зависит от той схемы выпрямления, которая применяется в конкретномслучае. Так, для однополупериодного и двухполупериодного выпрямителей U_b = π·Uо = 3.14·U_О, для мостового выпрямителя Ub = 2π·Uо/2 = 1,57·U_О, а для трехфазного выпрямителя U_b=2,1·Uо. При выборе диода, следовательно, должно соблюдаться условие U_обр ≥ U_b.

Рассмотрим примеры на составление схем выпрямителей.

Пример 8. Составить схему мостового выпрямителя, использовав один из четырех диодов: Д218, Д222, КД202Н, Д215Б. Мощность потребителя Ро = 300В, напряжение потребителя Uо = 200В.

Решение. 1. Выписываем из табл. 4 параметры указанных диодов и записываем их в таблицу.

Типы диодов	Iдоп, А	Uобр, В	Типы диодов	Iдоп, А	Uобр, В
Д218	0,1		КД202Н
Д222	0,4		Д215Б

2. Определяем ток потребителя Iо = Pо/ Uо = 300/200 = 1,5 A.

3. Находим напряжение, действующее на диод в непроводящий период для мостовой схемы выпрямителя, Ub = 1,57·Uo = 1,57·200 = 314В.

4. Выбираем диод из условия Iдоп> 0,5·Iо>0.5·1.5>0,75 А,Uобр>U_b ≥ 314 В. Эти условиям удовлетворяет диод КД202Н: Iдоп = 1,0> 0,75А; Uобр = 500 > 314В.

Диоды Д218 и Д222 удовлетворяют напряжению (1000 и 600 больше 314В), но не подходят по допустимому току (0,1 и 0,4 меньше 0.75А). Диод 215Б, наоборот, подходит по допустимому току (2 > 0.75А), но не подходит по обратному напряжению (200 < 314В).

5. Составляем схему мостового выпрямителя (рис. 5). В этой схеме каждый из диодов имеет параметры диода КД202Н; Iдоп = 1А; Uобр = 500В.

рис.5

рис. 6

Пример 9. Для питания постоянным током потребителя мощностью Ро =250Вт при напряжении Uо=100В необходимо собрать схему двухполупериодного выпрямителя, использовав стандартные диоды типа Д243Б.

Решение. 1. Выписываем из таблицы 4 параметры диода Iдоп = 2А; Uобр = 200В.

2. Определяем ток потребителя: Iо = Pо/ Uо = 250/100 = 2.5 A.

3. Определяем напряжение, действующее на диод в непроводящий период: U_b = 3,14Uо = 3,14·100 = 314 B.

4. Проверяем диод по параметрам Iдоп и Uобр. Для данной схемы диод должен удовлетворять условиям Uобр ≥ UВ и Iдоп> 0,5·Iо. В данном случае первое условие не соблюдается (200< 314), т.е. Uобр<U_b; второе выполняется (0,5·Iо = 0,5·2,5 = 1,25 <2 A).

5. Составляем схему выпрямителя. Чтобы выполнялось условие Uобр>U_b, необходимо два диода соединить последовательно, тогдаUобр = 200·2 = = 400 > 314В. Полная схема на рис. 6.

Пример 10. Для питания постоянным током потребителя мощностью Ро = 20В необходимо собрать схему однополупериодного выпрямителя, использовав имеющиеся стандартные диоды Д242А.

Решение. 1. Выписываем из таблицы 4 параметры диода: Iдоп = 10А, Uобр = 100В.

2. Определяем ток потребителяIо = Pо/ Uо = 300/200 = 15 A.

3. Определяем напряжение, действующее на диод в непроводящий период: U_b = 3,14·Uo = 3,14·20 = 63В.

4. Проверяем диод по параметра Iдоп и Uобр. Для данной схемы диод должен удовлетворять условиям Uобр>Ub, Iдоп>Iо. В данном случае второе условие не соблюдается (10 < 15А, т.еIдоп<Iо). Первое условие выполняется (100 > 63В).

5. Составляем схему выпрямителя. Чтобы выполнялось условие Iдоп>Iо, надо два диода соединить параллельно, тогда Iдоп =2·10 = 20А; 20>15А. Полная схема выпрямителя приведена на рис. 7.

Пример 11. Для составления схемы трехфазного выпрямителя на трех диодах заданы диоды Д243. Выпрямитель должен питать потребитель с Uо = = 150В. Определить допустимую мощность потребителя и пояснить составления схемы выпрямителя.

Решение. 1. Выписываем из таблицы 4 параметры диода: Iдоп = 5А, Uобр = 200В.

2. Определяем допустимую мощность потребителя. Для трехфазного выпрямителя Iдоп> ·Iо, т.е. Ро = 3Uо·I_доп=3·150·5 = 2250 Вт.

Следовательно, для данного выпрямителя Ро ≥ 2250 Вт.

3. Определяем напряжение, действующее на диод в непроводящий период: Ub = 2,1·Uo = 2,1·150 = 315В.

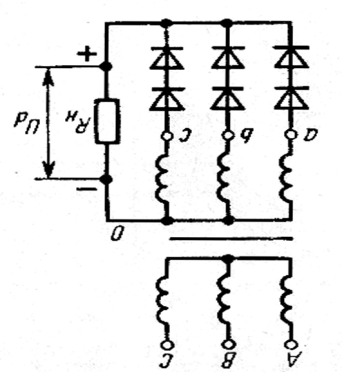4. Составляем схему выпрямителя. Проверяем диод по условию. В данном случае это условие не выполняется (200 < 315В). Чтобы это условие выполнялось, необходимо в каждом плече выпрямителя два диода соединить последовательно, тогда Uобр = 200·2 = 400В; 400 > 315В. Полная схема выпрямителя приведена рис. 8.