Лекция № 3. Системы линейных уравнений.
Основные понятия.
Системой линейных алгебраических уравнений, содержащей т уравнений и п неизвестных, называется система вида:
где числа аij,i = 1,т, j =1,п называются коэффициентами системы, числа bi – свободными членами. Подлежат нахождению числа хп.
Такую систему удобно записывать в компактной матричной форме А * Х = В.
Здесь А – матрица коэффициентов системы, называемая основной матрицей:
Произведение матриц А * Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (п штук).
Расширенной матрицей системы называется матрица 
системы, дополненная столбцом свободных членов
Решением системы называется п значений неизвестных х1 = с1, х2 = с2, …, хп = сп, при подстановке которых все уравнения системы обращаются в верными равенства. Всякое решение системы можно записать в виде матрицы-столбца
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместимой, если она не имеет ни одного решения.
Решение систем линейных уравнений.
Решение невырожденных линейных систем (определитель не равен 0). Метод Крамера
Пусть имеется система уравнений:
Обозначим через Δ определитель матрицы системы и через Δj определитель, который получается из определителя Δ заметой j-го столбца столбцом правых частей системы (j=1,2,...n).
Теорема.
1.3. Если определитель матрицы отличен от нуля, т.е. Δ ≠0, то система имеет единственное решение, которое находится по формуле: 
Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
- Вычисляем определитель основной матрицы системы, убеждаемся, что он отличен от нуля.
- Находим определители Δj, которые являются определителями матриц, полученных из матрицы А заменой k-ого столбца (k = 1, 2, …, n) на столбец свободных членов.
- Вычисляем искомые неизвестные переменные x1, x2, …, xn по формулам.
- Выполняем проверку результатов, подставляя x1, x2, …, xn в исходную СЛАУ. Все уравнения системы должны обратиться в тождества. Можно также вычислить произведение матриц A ⋅ X, если в результате получилась матрица, равная B, то решение системы найдено верно. В противном случае в ходе решения была допущена ошибка.
Матричный способ (с помощью обратной матрицы)
Пусть дана система п линейных уравнений с п неизвестнымиили в матричной форме А * Х = В.
Найдём решение данной системы уравнений в случае ∆ ≠ 0.
Умножив обе части уравнения А * Х = В слева на матрицу А-1, получим А-1 * А * Х = А-1 * В. Поскольку А-1 * А = Е и Е * Х = Х, то Х = А-1 * В.
Пример 4.3. Решить систему 
Решение: 
Значит, 
Задание 1. При помощи формул Крамера найти решение системы 
Решение. Вычисляем определитель матрицы системы:
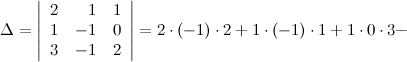
Так как определитель матрицы системы неравен нулю, то по теореме Крамера система совместна и имеет единственное решение. Для его нахождения вычислим следующие определители:
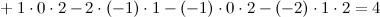
Таким образом,
2) Найдите решение системы линейных уравнений методом Крамера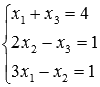 
. 
Решение.
Перепишем систему в виде, чтобы стало видно основную матрицу системы. Найдем ее определитель по формуле
Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители 
:
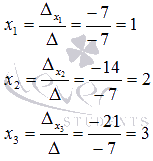
Ответ:
.
Обозначения неизвестных переменных в уравнениях системы могут отличаться от x1, x2, …, xn. Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.
3) Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными 
.
Решение. – Домашнее задание
В данном примере неизвестные переменные имеют другое обозначение (x, y и z вместо x1, x2 и x3). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать. Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как 
. Теперь основную матрицу системы хорошо видно 
.
Дополнительные примеры: