Количественное число а является результатом счета элементов конечного множества: а= n(А). С другой стороны а= n(В), т.е. А и В равномощны. Отношение «быть равномощными» является отношением эквивалентности, поэтому все множества разбиваются на классы эквивалентности и в каждом классе собраны множества одинаковой мощности. Теперь мы можем сказать, что натуральное число а является общим свойством всех равномощных множеств. Каждый класс может быть задан одним представителем.Число 2 - общее свойство класса множеств, равномощных числу рук у человека, числу крыльев у птицы. О числе 4 можно сказать, что это общее свойство множеств, равномощных числу сторон квадрата, числу граней тетраэдра,числу ножек у стула и т.д.Нуль с теоретико-множественной позиции есть число элементов пустого множества Ø.
Итак, натуральное число а как характеристику количества можно рассматривать с двух позиций:
1) как число элементов во множестве А, получаемое при счете элементов, причем A ~Na.
2) Как общее свойство класса конечных равномощных множеств.
Число «нуль» с теоретико-множественных позиций рассматривается как число элементов пустого множества: 0= n(Ø)
Введем отношение «быть меньше» с ТМ позиций.
В аксиоматической теории: a<b<=> 
с 
N,(a+c=b)
Если a<b, то это означает, что отрезок натурального ряда Na является собственным подмножеством отрезка Nb: а=n(A), A ~Na, b =n(B), В ~N b, Na 
N b. Справедливо обратное утверждение: если Na N b, т.е. если Na является собственным подмножеством множества N b, то a<b.
Например: {1,2,3,4} {1,2,3,4,5,6,7}, N4 N7.
Na
А: 
В: 
N b
В школьной терминологии определение отношения «меньше» формулируется следующим образом: «Число а меньше числа b тогда и только тогда, когда при счете число а называют раньше числа b ».
Можно сказать, что а< b, если во множестве В можно выделить собственное подмножество, равномощное множеству А. 0<а истинно для любого натурального числа, т.к. Ø содержится в любом множестве.
Теоретико- множественный смысл суммы.
Теорема 1. Пусть А и В - конечные множества, не имеющие общих элементов. Тогда их объединение тоже конечно и n(A 
B)=n(A)+n(B). Предварительно докажем, что 
a Nи b 
N N b ~X={x/ а+1 ≤х ≤ а+ b }.
1 2 3 4 5 6
• • • • • • Nb~ Х b = 6, а =3
• • • • • •
4 5 6 7 8 9
б) Пусть n(A)=a, n(В)=b. Тогда существует взаимно-однозначное отображение множества А на множество Na и множества В на N b,a N b можно взаимно однозначно отобразить на множество X.
А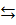 
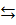Na, В Nb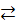 
Х = {х | а+1 ≤ х ≤ а+b }
N(А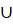 
В) = n (А) + n(В) = а + b
Таким образом, сумма натуральных чисел а и b с теоретико- множественной позиции представляет собой число элементов в объединении конечных непересекающихся множеств таких, что a = n(A), b = n(В).
Смысл а+0=а: А Ø=А =>n(А Ø) = n(А) = а.
Свойства: a + b = b + a следует из того, что А В = В А. Тогда n(А В) = n(В А). Свойство транзитивности a+(b+c)=(a+b)+c следует из того, что А (В С) = (А В) С для непересекающихся множеств.
Теоретико-множественный смысл разности.
По аксиоматической теории а – b = с<=> ( с N, c + b = a).
Теорема 2. Пусть А -конечное множество, В - его собственное подмножество, тогда А-В тоже конечно, причем n(A-B)=n(A)-n(B)
А = В (В \ А) =>n(А) = n(В) + n(В \ А) =>n(В \ А) = n(А) – n(В)= а - b
А \ В
В
Таким образом, разность натуральных чисел а и b представляет собой число элементов в дополнении подмножества В до множества А, т.е. а-b= п(А)- п(В)= n(А\В), если В 
А, В≠А, В≠0.
а-0=а следует из того, что А\ Ø =А => п(А\Ø)= п(А)
Отношение «больше на », «меньше на».
В аксиоматической теории: а <b<=> с N, а + с = b.
(число а меньше числа b на с единиц).
С ТМ позиции а <b на с единиц означает, что если а = n(А), b = n(В), то в множестве В содержится столько элементов, сколько их в А и еще с элементов. т.к. с = n(В \ В1), где В1 В, n(В) = b, n(А) = а, то по определению разности с = b – а
В
А ~ В1
В1
Теоретико-множественный смысл произведения.
По аксиоматической теории: а · b – алгебраическая операция, обладающая свойствами: а · 1 = а, а ·b′ = а b + а.
В школьном курсе используется другое определение умножения:
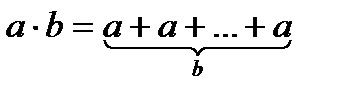, т.е. а · b – есть сумма bслагаемых, каждое из которых равно а.
Эти определения равносильны, т.к.
1. а · 1 = а
2. 
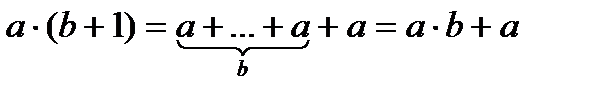
3. а · 0 = 0
Определение умножения целых неотрицательных чисел.
Если а, b –целые неотрицательные числа, то произведением чисел а · b называется число, удовлетворяющее следующим условиям:
1. 
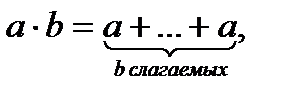если b> 1
2. а · b = а, если b = 1
3. а · b = 0, если b = 0
Случаю 1 можно придать теоретико-множественную трактовку.
Если множества А1, А2 …Аb имеют по а элементов каждое, причем никакие два из них не пересекаются, то их объединение А1 
А2 А3 … А bсодержат а ·b элементов.
Таким образом, с теоретико-множественной позиции произведение
а · b (b> 1) представляет собой число элементов в объединении b множеств, каждое из которых содержит по а элементов и никакие два из них не пересекаются:
а · b = n(А1 А2 … Аb), если n(Аi) = а и А1, А2 …. Аb попарно не пересекаются.
Другое истолкование произведения а · b.
Теорема 3. Пусть А и В конечные множества. Тогда их декартово произведение также является конечным множеством, причем выполняется равенство n(А 
В) = n(А) n(В).
Доказательство.
А В = {(а1b1); (а1b2)… (а2b1)(а2b2)…, (аnвk)}
Пар с первым элементом k штук
Пар с вторым элементом k штук n · k = n(А) · n(В)
Пар с n - ым элементом k штук
Рассмотреть обоснование свойств а · b = b · а, а(bс) = (аb)с через свойства декартова произведения.
А В равномощно В 
А
А (В С) ~ ((А В) С)
А (В С) = (А В) (А С)
А (В \ С) ~ (А В) \ (А С)
Теоретико-множественный смысл частного.
В аксиоматической теории деление определяется как операция, обратная умножению.
а · b = с =>с: а = в или с: b = а.
Если произведение а · b с ТМ точки зрения представляет собой число элементов в объединении в попарно непересекающихся множеств, в каждом из которых содержится а элементов, тогда частное с: а – это число подмножеств в разбиении множества А, а с: b – число элементов в каждом подмножестве этого разбития.
Задача: 12 карандашей разложили в 3 коробки поровну. Сколько карандашей в каждой коробке?
Младшие школьники при решении задач встречаются с отношениями «больше b», «меньше b».
В аксиоматической теории определение этих отношений вытекает из определения деления натуральных чисел: а:b = с, то можно говорить, что «а больше b в с раз» или «b меньше а в с раз».
Если а = n(А), b = n(В) и известно, что а меньше b в с раз, то множество В можно разбить на с подмножеств, каждое из которых равномощно а.
b: а = с
Если в множестве В элементов в 2 раза больше чем в множеств А, то множество В можно разбить на два подмножества, равномощных А.
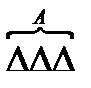
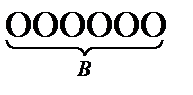
Теоретико -множественное истолкование можно дать и делению с остатком.
Напомним, что разделить натуральное число a на натуральное число bс остатком – это значит найти такие целые неотрицательные числа q и r, что a=bq+r, где 0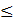 
r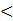 
b.Пусть a=n(A) и множество А разбито на А1, А2, А3,….Аq, R так, что множества
А1, А2, А3,….Аq равночисленны, а множество Rсодержит меньше элементов, чем каждое из множеств Аi. Тогда, если n(A1)=n(A2)=…n(Aq)=b,а n(R)=r, то a=bq+r, где 0 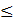r 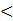b, q – неполное частное при делении a на b, а b –остаток при этом делении.