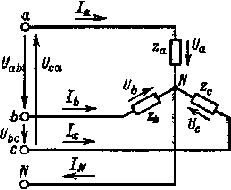
Как видно из схемы рис. 3.7, при соединении звездой фазные напряжения приемника Ua, Ub и Uc не равны линейным напряжениям Uab, Ubc и Uca. Применяя второй закон Кирхгофа и к контурам aNba, bNcb и cNac, можно получить следующие соотношения между линейными и фазными напряжениями:
(3.8a)
U ab = U a - U b , U bс = U b - U с, U ca = U c - U a .
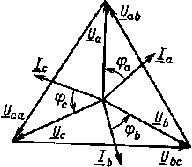
Пользуясь соотношениями (3.7) и имея векторы фазных напряжений, нетрудно построить векторы линейных напряжений (рис. 3.8).
|
| Рис. 3.7. Схема соединения фаз приемника звездой |
Если не учитывать сопротивлений линейных проводов и нейтрального провода, то следует считать комплексные значения линейных и фазных напряжений приемника равными соответственно комплексным значениям линейных и фазных напряжений источника. Вследствие указанного равенства векторная диаграмма напряжений приемника не отличается от векторной диаграммы источника при соединении звездой (см. рис. 3.5, б и 3.8). Линейные и фазные напряжения приемника, как и источника, образуют две симметричные системы напряжений. Очевидно, между линейными и фазными напряжениями приемника существует соотношение, подобное (3.6), т. е.
(3.9)
U л = √3 U ф.
|
| Рис. 3.8. Векторная диаграмма при соединении приемника звездой в случае симметричной нагрузки |
Как будет показано далее, соотношение (3.9) справедливо при определенных условиях так же в случае отсутствия нейтрального провода, т. е. в трехпроводной цепи.
На основании указанного соотношения можно сделать вывод о том, что соединение звездой следует применять в том случае, когда каждая фаза трехфазного приемника или однофазные приемники рассчитаны на напряжение в √3раз меньшее, чем номинальное линейное напряжение сети.
Из схемы рис. 3.7 видно, что при соединении звездой линейные токи равны соответствующим фазным токам:
(3.10)
I л = I ф.
С помощью первого закона Кирхгофа получим следующее соотношение между фазными токами и током нейтрального провода:
(3.11)
I a + I b + I c= I N .
Имея векторы фазных токов, с помощью (3.11) нетрудно построить вектор тока нейтрального провода.
Если нейтральный провод отсутствует, то, очевидно,
I a + I b + I c= 0.
Нагрузка считается симметричной, когда равны в отдельности активные и реактивные сопротивления всех фаз:
ra = rb = rc и ха = хb = хc,
где ха = хLа - хCа и т. д.
Условие симметричности нагрузки может быть записано также через комплексные значения полных сопротивлений фаз: Z a = Z b = Z c .
Симметричная нагрузка трехфазной цепи возникает при подключении к сети трехфазных приемников (см. § 3.1).
Будем считать сначала, что при симметричной нагрузке имеется нейтральный провод.
В отношении любой фазы справедливы все формулы, полученные ранее для однофазных цепей. Например, для фазы a
(3.12)
| } |
Так как в четырехпроводной цепи Ua = Ub = Uc =U ф = U л / √3, то, очевидно, при симметричной нагрузке
Ia =Ib =Iс =I ф; φ a = φ b = φ c = φф ; Pa =Pb,Pс =P ф ;
Qa =Qb =Qс =Q ф ; Sa =Sb =Sс =S ф.
Векторная диаграмма при симметричной активно-индуктивной нагрузке приведена на рис. 3.8.
Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке образуется симметричная система токов, поэтому ток в нейтральном проводе IN = Ia + Ib + Ic = 0.
Очевидно, отключение нейтральною провода при IN = 0 не приведет к изменению фазных напряжений, токов, углов сдвига фаз, мощностей и векторной диаграммы. Даже при отсутствии нейтрального провода фазные напряжения оказываются равными U ф = U л / √3, т. е. тому напряжению, па которое рассчитаны фазы трехфазного приемника.
Из сказанного следует, что при симметричной нагрузке в нейтральном проводе нет необходимости и при симметричной нагрузке нейтральный провод не применяется.
Мощности трехфазного приемника могут быть выражены так:
(3.13)
| } |
В качестве номинальных напряжений и токов трехфазных приемников указываются обычно линейные напряжения и токи. Учитывая это, мощности трехфазных приемников целесообразно также выражать через линейные напряжения и токи. Заменив в (3.13) фазные напряжения и ток согласно (3.8) и (3.9), получим
(3.14)
| } | |||