Переходя к оригиналу, получим переходный процесс в виде:
 L-1
L-1  L-1
L-1 
 .
.
Однако, производить непосредственное интегрирование затруднительно, поэтому для нахождения переходного процесса по его изображению для случаев, когда изображение переходного процесса является правильной рациональной дробью
 ,
,
следует применить теоремы Хевисайда (теоремы разложения).
Например, если корни характеристического уравнения 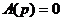 действительные простые, отличные от нуля, то
действительные простые, отличные от нуля, то
 ,
,
где
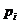 -
- 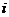 -ый корень характеристического уравнения
-ый корень характеристического уравнения 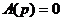 ,
,
 ,
,
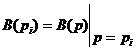
3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ АСР
3.1. Комплексная частотная функция
Предположим, что АСР описывается уравнением:
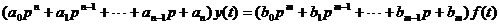 ,
,
где
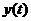 - регулируемая величина;
- регулируемая величина;
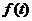 - приложенное к системе возмущающее воздействие.
- приложенное к системе возмущающее воздействие.
Допустим, что входное воздействие – синусоидальное колебательное, описываемое уравнением:
 ,
,
где
 -амплитуда колебаний;
-амплитуда колебаний;
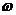 -частота колебаний,
-частота колебаний,  .
.
В этом случае, в соответствии с принципом суперпозиции, спустя некоторое время после приложения входного воздействия на выходе системы установятся синусоидальные колебания с такой же частотой, но отличные по модулю и фазе.
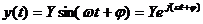
где
 амплитуда;
амплитуда;
 сдвиг фаз.
сдвиг фаз.
Продифференцируем входную 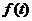 и выходную
и выходную 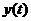 функции:
функции:


Подставив далее значения функций и их производных в исходное уравнение и разделив выходную величину на входное воздействие, получим:

Величину 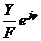 называют комплексной частотной функцией.
называют комплексной частотной функцией.
Комплексная частотная функция является отношением вынужденного движения на выходе системы к входному гармоническому воздействию.
Сравнивая выражение комплексной частотной функции с передаточной функцией, можно увидеть, что комплексная частотная функция является частным случаем передаточной функции, когда комплексная переменная  является чисто мнимой величиной
является чисто мнимой величиной  .
.
Обозначив комплексную частотную функцию через  , можно записать:
, можно записать:




Комплексная частотная функция представляет собой вектор в комплексной плоскости (Рис.3.1)
 |

 |








 0
0 
 |

Рис. 3.1
Вектор характеризуется амплитудой (А) и фазой ( ). Амплитудой (модулем) вектора является его длина. Фаза вектора – угол между положительной вещественной полуосью и направлением вектора.
). Амплитудой (модулем) вектора является его длина. Фаза вектора – угол между положительной вещественной полуосью и направлением вектора.
Если изменять частоту входных колебаний от 0 до  , то получим ряд векторов в комплексной плоскости, концы которых опишут некоторую кривую, называемую годографом. Годограф вектора комплексной частотной функции при изменяющейся частоте в пределах
, то получим ряд векторов в комплексной плоскости, концы которых опишут некоторую кривую, называемую годографом. Годограф вектора комплексной частотной функции при изменяющейся частоте в пределах  , называют амплитудно-фазовой частотной характеристикой (АФХ).
, называют амплитудно-фазовой частотной характеристикой (АФХ).
В соответствии с рисунком 3.1 различают частотные характеристики:
1. Вещественная частотная характеристика  - проекция вектора на вещественную полуось.
- проекция вектора на вещественную полуось.
2. Мнимая частотная характеристика  - проекция вектора на мнимую полуось.
- проекция вектора на мнимую полуось.
3. Амплитудно-частотная характеристика  .
.
4. Фазо-частотная характеристика  .
.
Между приведенными частотными характеристиками имеются однозначные зависимости:


3.2 Переходная функция
Переходной функцией называют изменение во времени выходной величины системы в результате приложения к ней единичного скачкообразного входного воздействия.
Обозначив переходную функцию через  и соответствующее ей изображение через
и соответствующее ей изображение через  , можно записать:
, можно записать:
 ;
;
 .
.
3.3 Весовая функция
Весовой функцией 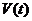 называют реакцию системы на импульсную возмущающую функцию
называют реакцию системы на импульсную возмущающую функцию  .
.
Так как  , то
, то  , т.е. изображение импульсной функции равно единице.
, т.е. изображение импульсной функции равно единице.
Тогда 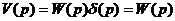 , т.е. изображение весовой функции равно передаточной функции. Весовая функция записывается как:
, т.е. изображение весовой функции равно передаточной функции. Весовая функция записывается как:
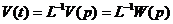 .
.
4. ТИПОВЫЕ ЗВЕНЬЯ АСР
4.1. Введение
Любая АСР состоит из реальных физических элементов, отличающихся друг от друга своими физическими свойствами. Однако, многие из них, будучи различными по своей физической сущности, могут быть описаны одинаковыми математическими уравнениями. Это дает возможность классифицировать объекты и отдельные элементы системы в целом по их математическому описанию.
4.2. Безынерционное звено
К таким звеньям относят физические элементы, описываемые уравнением:
 .
.
Коэффициент пропорциональности  называют коэффициентом передачи.
называют коэффициентом передачи.
Его размерность определяется размерностями выходной 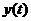 и входной
и входной 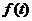 величин:
величин:
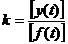 .
.
Преобразовав уравнение по Лапласу:
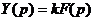 ,
,
получим
 ,
,
т.е. передаточная функция звена равна его коэффициенту передачи.
Амплитудно-фазовая характеристика звена:


представляет собой точку на вещественной полуоси комплексной плоскости на расстоянии  от начала координат (Рис. 4.1).
от начала координат (Рис. 4.1).
 |


 K
K
 |
0 
Рис.4.1.
Переходная функция:

представляет собой скачкообразную функцию высотою  (Рис.4.2)
(Рис.4.2)
 h
h
 |
k
 0 t
0 t
Рис. 4.2.
Весовая функция  представляет собой импульсную функцию (Рис.4.3).
представляет собой импульсную функцию (Рис.4.3).
 V
V
 |
 0 t
0 t
Рис.4.3.
4.3. Идеальное дифференцирующее звено
К ним относят элементы АСР, у которых выходная величина пропорциональна производной входного воздействия:
 ,
,
где Т - коэффициент пропорциональности, имеющий размерность времени и
называемый постоянной дифференцирования.
Преобразовав уравнение по Лапласу, получим:
 и
и  .
.
АФХ звена


является прямой, совпадающей с верхней мнимой полуосью комплексной плоскости (Рис.4.4).

 )
)
 |
 900
900
 |
0 
Рис.4.4.
Переходная функция звена:

представляет собой импульсную функцию (Рис.4.5).
 h
h
 |
0 t
Рис.4.5.
Весовая функция звена  является импульсной функцией второго рода (Рис.4.6).
является импульсной функцией второго рода (Рис.4.6).
 V
V
 | |||
 | |||
 0 t
0 t
Рис.4.6.
4.4. Идеальное интегрирующее звено
Такими звеньями называют элементы АСР, у которых выходная величина пропорциональна интегралу от входного воздействия:
 .
.
Это уравнение можно записать и в виде:
 .
.
Отсюда вытекает физический смысл коэффициента пропорциональности:
 .
.
Коэффициент пропорциональности  является скоростью изменения выходной величины, приведенной к единице возмущающего воздействия. В связи с этим величину
является скоростью изменения выходной величины, приведенной к единице возмущающего воздействия. В связи с этим величину  называют приведенной скоростью.
называют приведенной скоростью.
Преобразовав исходное уравнение по Лапласу, получим:
 и
и  .
.
АФХ звена


является прямой, совпадающей с нижней мнимой полуосью комплексной плоскости (Рис. 4.7).



 |
0 900 
 ω
ω
Рис.4.7.
Переходная функция звена

является прямой линией с угловым коэффициентом  (Рис. 4.8)
(Рис. 4.8)
 h
h 
 |

 t
t
0
Рис.4.8.
Весовая функция звена  представляет собой скачкообразную функцию высотой
представляет собой скачкообразную функцию высотой  (Рис.4.9).
(Рис.4.9).
 V
V
 |

 0 t
0 t
Рис.4.9.
4.5. Апериодическое звено первого порядка
К таким звеньям относят физические элементы, описываемые дифференциальным уравнением первого порядка:
 ,
,
где
 -коэффициент передачи;
-коэффициент передачи;
 -постоянная времени.
-постоянная времени.
Преобразовав уравнение по Лапласу:
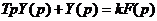 ,
,
получим передаточную функцию звена:
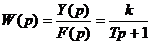 .
.
АФХ звена

 ,
,
где
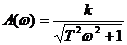 ,
,  .
.
Амплитудно-фазовая характеристика представляет собой полуокружность, расположенную в четвертом квадранте комплексной плоскости (Рис.4.10)





 K
K 

0 900 
Рис.4.10.
Переходная функция звена:
 ,
, 
Так как
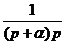 =
=  ,
,
то
 .
.
График переходной функции приведен на рисунке 4.11 а. Она представляет собой возрастающую экспоненту.

 h v
h v
 |







 K
K 
0 t 0 t
а) б)
Рис.4.11.
Весовая функция звена 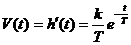 является положительной убывающей по модулю экспонентой (Рис.4.11б).
является положительной убывающей по модулю экспонентой (Рис.4.11б).
4.6. Реальное дифференцирующее звено
К таким звеньям относят элементы АСР, описываемые дифференциальным уравнением:
 .
.
Преобразовав его по Лапласу
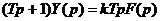 ,
,
получим передаточную функцию
 .
.
Отсюда

 ,
,
где
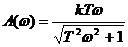 ,
,
 .
.
При 
 ,
,  . При
. При 
 ,
, 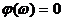 .
.
АФХ является полуокружностью, расположенной в первом квадранте комплексной плоскости (Рис.4.12).




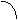

 900
900 
 |
 0
0 
K
Рис.4.12.
Переходная функция звена
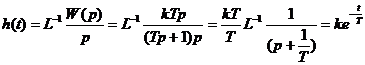
является положительной убывающей экспонентой (Рис. 4.13а).

 h V
h V
 | |||
 |

 0 t
0 t