 - передаточная функция элементов прямой цепи при единичном
- передаточная функция элементов прямой цепи при единичном
коэффициенте передачи.
Тогда
 .
.
При достаточно большом значении коэффициента передачи прямой цепи (теоретически при Кпр  ) получим:
) получим:
 .
.
Контур с обратной связью при достаточно большом коэффициенте передачи прямой цепи называют предельной системой.
Динамические свойства предельной системы определяются динамическими свойствами обратной связи.
5. Основные свойства типовых объектов регулирования
5.1 Статические и астатические объекты регулирования
С учетом явления запаздывания передачи входного сигнала уравнение, описывающее динамику одномерного объекта, можно записать в виде:

 ,
,
где
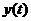 -регулируемая величина;
-регулируемая величина;
 -основное возмущающее воздействие (нагрузка объекта);
-основное возмущающее воздействие (нагрузка объекта);
t -величина запаздывания.
Преобразовав уравнение по Лапласу, получим:

 .
.
Запишем уравнение в виде:

или
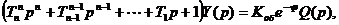
где
 -коэффициент передачи объекта;
-коэффициент передачи объекта;
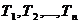 -постоянные времени.
-постоянные времени.
Левый многочлен уравнения можно записать в виде сомножителей первой степени.
Тогда
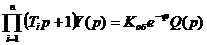
и
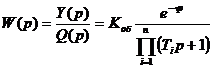 .
.
Следовательно, в этом случае объект структурно может быть представлен в виде последовательного соединения звена транспортного запаздывания и апериодических звеньев первого порядка (рис. 5.1).




 q(t) y(t)
q(t) y(t)






 Wt(p) W1(p) W2(p) … Wn-1(p) Wn(p)
Wt(p) W1(p) W2(p) … Wn-1(p) Wn(p)
Рис.5.1.
Объект статичен, так как в установившемся режиме имеется однозначная зависимость между выходным сигналом и входным воздействием

Если в левой части исходного уравнения отсутствует свободный член 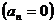 , то в установившемся режиме не будет однозначной зависимости между выходом и входом, т.е. объект астатический. В этом случае
, то в установившемся режиме не будет однозначной зависимости между выходом и входом, т.е. объект астатический. В этом случае
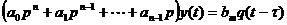 .
.
Это уравнение можно записать в виде:

или

где  - постоянные времени;
- постоянные времени;
Отсюда
 .
.
Следовательно, астатический объект регулирования может быть структурно представлен в виде последовательного соединения звена транспортного запаздывания, интегрирующего звена и апериодических звеньев первого порядка
(рис. 5.2).



 q(t) y(t)
q(t) y(t)





 Wt(p) Wu(p) W1(p) … Wn(p)
Wt(p) Wu(p) W1(p) … Wn(p)
Рис.5.2.
Подставив в передаточные функции  , получим аналитические выражения АФХ объектов.
, получим аналитические выражения АФХ объектов.

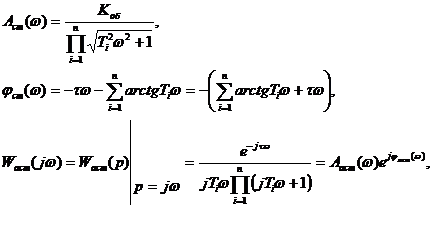

Графики АФХ объектов регулирования приведены на рисунке 5.3 а,б.





 Коб
Коб



 0
0 





 0
0 
 0
0
а) статический ОР б) астатический ОР
Рис.5.3.
Переходные характеристики статического и астатического объектов приведены на рисунке 5.4 а,б.


 h h
h h
 |





 0
0  t 0
t 0  t
t
 | |||
 | |||
а) статический ОР б) астатический ОР
Рис.5.4.
5.2. Экспериментальное определение временных динамических характеристик объектов регулирования
Для получения временной динамической характеристики объекта регулирования организуют эксперимент.
В какой-то момент времени к объекту регулирования, находящемуся в установившемся режиме работы, прикладывают некоторое возмущающее воздействие и затем регистрируют отклонения регулируемой величины во времени до ее восстановившегося значения с помощью соответствующего измерительного прибора.
Перед началом эксперимента нужно убедиться в том, что объект регулирования находится в установившемся режиме работы. Для достоверности измеренных отклонений регулируемой величины необходимо один и тот же опыт повторять 2-3 раза.
В найденную путем эксперимента динамическую характеристику объекта включены характеристика собственно объекта и характеристика регистрирующего прибора.
В связи с этим желательно в качестве датчиков отклонений физических величин от их номинальных значений применять те, которые входят в измерительный блок регулирующего устройства, поддерживающего на каком-то значении данную физическую величину.
В качестве возмущающих воздействий могут быть использованы типовые функции, некоторые из которых приведены в таблице 5.1.
Таблица.5.1.
| №п/п | Возмущение f(t) | График f(t) | Изображение F(p) |
| 1. 2. 3. 4. | Ступенчатое при
высоте ступени h
П-образное при высоте h и при длительности 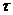 Ступенчатое при высоте h и времени нанесе-ния возмущения
Ступенчатое при высоте h и времени нанесе-ния возмущения 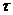 Треугольное при высоте h и времени нанесе-ния возмущения
2
Треугольное при высоте h и времени нанесе-ния возмущения
2 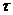
| f
h
0 t
f
h
0 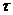 t
f h
0 t
f h
0 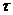 t
f
h
0
t
f
h
0 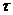 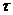 t t
| 



|
Наиболее часто при определении динамических свойств объекта регулирования применяют ступенчатое возмущающее воздействие (строка 1 табл.5.1), т.е. экспериментально находят переходную функцию объекта.
5.3. Определение передаточной функции объекта регулирования по его экспериментальной переходной функции
5.3.1. Статический объект регулирования
5.3.1.1. Структурное представление статического объекта последовательным соединением апериодического звена первого порядка и звена запаздывания
В общем виде переходный процесс в объекте, как реакция на ступенчатое возмущение, приведен на рисунке 5.5 а.
Для удобства использования этого процесса при нахождении передаточной функции объекта, его (процесс) представляют приведенным к единичному ступенчатому возмущению, т.е. переходной характеристикой, как реакцией на единичное ступенчатое возмущение (рис. 5.5 б).
 f
f




 h
h 
 0 t
0 t
 y h(t)
y h(t)
 y(t)
y(t)

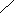









 = A
= A 







 0
0  t 0
t 0 
 t
t





а) б)
Рис.5.5.
При представлении объекта простейшей моделью в виде последовательного соединения звена запаздывания и апериодического первого порядка передаточная функция запишется как:
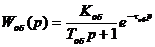 .
.
Параметры передаточной функции  и tоб=t0+tе находятся из графика переходной функции, как показано на рисунке 5.5 б.
и tоб=t0+tе находятся из графика переходной функции, как показано на рисунке 5.5 б. 
5.3.1.2. Структурное представление статического объекта последовательным соединением звена запаздывания и апериодического звена второго порядка
При такой модели объекта
 .
.
Значения Коб и t0 (чистое запаздывание) определяются сразу же из графика переходной функции (рис. 5.6).
Для определения коэффициентов передаточной функции Т1 и Т22 на графике переходной функции находят точку перегиба (т. А) и определяют ее координаты (t0+tn),
 ;проводят касательную к кривой
;проводят касательную к кривой  в точке перегиба; определяют численные значения Т1, Тоб и рассчитывают F1, F2, F=F1+F2, причем площадями являются:
в точке перегиба; определяют численные значения Т1, Тоб и рассчитывают F1, F2, F=F1+F2, причем площадями являются:
F1 –площадь, ограниченная кривой  , ее асимптотой h(∞) и прямой, проведенной
, ее асимптотой h(∞) и прямой, проведенной
через точку перегиба параллельно оси ординат;
F2 –площадь, ограниченная кривой  , ее асимптотой h(∞) и прямыми,
, ее асимптотой h(∞) и прямыми,
проведенными параллельно оси ординат на расстояниях t=t0 и t=t0+tn от начала
координат;
 h
h
Tоб



 F2 T1 F1 F1+F2=F
F2 T1 F1 F1+F2=F




 B C
B C

















 h(t)
h(t)









 A
A
hп



 0
0 
 t
t
Рис.5.6.
После произведенных построений находят

 или
или  .
.
Коэффициент Т1 может быть определен, как длина (в размерности времени) проекции касательной к переходной характеристике в точке перегиба на асимптоту кривой  .
.
5.3.1.3. Определение передаточной функции статического объекта по его экспериментальной переходной характеристике методом Симою (методом площадей)
Статический объект регулирования в общем случае может быть описан линейным дифференциальным уравнением с постоянными коэффициентами или передаточной функцией вида

которая с желаемой степенью точности может быть аппроксимирована дробно-рациональной функцией

Из этих уравнений имеем
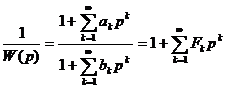 .
.
Отсюда

или

где

Здесь  - нормированная переходная функция.
- нормированная переходная функция.
Введя безразмерное время  ,
,  и заменив переменную, получим:
и заменив переменную, получим:
 .
.
Это выражение позволяет вычислить любой коэффициент  .
.
Например, при к=1

при к=2

при к=3

Из этих уравнений вытекает геометрический смысл коэффициентов F1, F2, …,Fк.
Коэффициент F1 является площадью, ограниченной нормированной кривой переходной функции, осью ординат и линией установившегося значения функции
 (рис. 5.7).
(рис. 5.7).




 F1
F1


 F1 F2
F1 F2




















 1 F1(∞)
1 F1(∞)
 | |||
 | |||