Элементы специальной теории относительности
Механический принцип относительности утверждает:
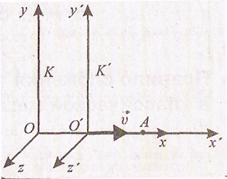
законы динамики одина-ковы во всех инерциальных системах отсчета. Система К' движется относительно инерциальной системы К равномерно и прямолиней-но со скоростью u
(u = const). Скорость u направлена вдоль 00'.
ro = ut.
Преобразования координат Галилея задают связь между радиусами-векторами или координатами произвольной точки А в обеих системах '
Правило сложения скоростей в классической механике при переходе от одной и.с.о. к другой и.с.о.
Продифференцировав по времени
и учитывая, что в классической механике t = t', получаем
Ускорение
Это значит,что система К' инерциальна (точка А дви-жется относительно ее равномерно и прямолинейно). Это и есть доказательство механического принципа относительности.
Эти соотношения справедливы лишь в классической механике (v «с).
Постулаты Эйнштейна
I. Принцип относительности:
никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы отсчета, не дают воз-можность обнаружить, покоится ли эта система или движется равномерно и прямолинейно; всезаконы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.
II, Принцип инвариантности скорости света: скорость света в вакуумене зависит от скорости движения источника света или наблюдателя и
одинакова во всех инерциальных системах отсчета.
Согласно постулатам Эйнштейна постоянство скорости света — фундаменталъное свойство природы, которое констатируется как опытный факт,
Преобразования Лоренца (при v ≈ с)
Система К' движется относительно системы К со скоростью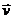 
= const
Преобразования Лоренца имеют следующий вид:
1) Эти уравнения симметричны и
отличаются лишь знаком при v, что
очевидно.
2) При v<<c они переходят в классические преобразования Галилея.
3) В закон преобразования координат входит время, а в закон преобразования времени — пространственные координаты,тем самым устанавлена взаимосвязь прос-транства и времени.
Из преобразований Лоренца следует:
Относительность одновременности
Пусть в системе К в точках с координатами х1, и х2 в моменты времени t1, и t2 происходят два события. В системе К' им соответствуют координаты x'1 и х'2 и моменты t'1 и t'2. Если события в системе К происходят в одной точке (х1=х2) и являются одновременными (t1=t2), то, согласно преобразованиям Лоренца.
x'1= х'2 и t'1= t'2.
т. е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета.
Если события в системе К пространственно разобщены (х1 ≠ х2), но одновременны (t1 = t2), то в системе К', согласно преобразованиям Лоренца,
Таким образом, в системе К' эти события, оставаясь пространственно разобщенными, оказываются и неодновременными.
Длительность событий в разных системах отсчета
Пусть в некоторой точке (с координатой х), покоящейся относительно системы K, происходит событие, длительность которого (разность показаний часов в конце и начале события) 
= t2 – t1, где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К'
(1)
где
Подставив в (1),получаем
< ', т. е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т. е. ход часов замедляется в системе отсчета,относительно которой часы движутся.
Длинател в разных системах отсчета
длина стержня в системе К:
длина стержня в системе К'
Размер тела,движущегося относительно инерциальной системы отсчета, уменьшается в направлении движении в раз,
т. е. лоренцево сокращение длины тем больше, чем больше скорость движения.
Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех и.с.о.