ЧАСТЬ 1 ЭЛЕКТРОТЕХНИКА
Тема 1 Цепи однофазного переменного тока
Переменный ток Основные понятия и определения
В технике переменный ток – это ток, периодически изменяющийся по величине и направлению (обычно по синусоидальному закону).
Мгновенное значение ЭДС в витке генератора переменного тока
e = Emsin(wt + y)
Em – амплитуда (максимальное значение гармонической функции)
(wt + y) – фаза колебания
y – начальная фаза (при t = 0)
T – период колебания (время полного цикла колебания)
f = 1 / T – циклическая частота (число циклов в сек.)
w = 2p / T = 2pf – угловая частота – скорость изменения фазы колебания.
Для различных значений ЭДС, тока и напряжения принято использовать следующие обозначения:
e, i, u – мгновенные значения ЭДС, тока и напряжения
Em, Im, Um – амплитудные значения ЭДС, тока и напряжения
Eср, Iср, Uср – средние значения ЭДС, тока и напряжения
E, I, U – действующие значения ЭДС, тока и напряжения.
Среднее значение синусоидального тока характеризует изменение заряда за время D t (DQ = Iср Dt)
Известно, что среднее значение любой гармонической функции за период равно нулю. Поэтому принято определять среднее значение переменного тока на интервале Т/2. После простейшего интегрирования получим:
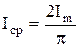
Средние значения дают возможность легко рассчитать суммарный заряд при электролизе, при зарядке аккумулятора, при анализе выпрямительных устройствах и т.д.
Действующее значение переменного тока I равно такому постоянному току I0, который обеспечивает равное тепловое или энергетическое воздействие. Если посчитать энергию постоянного и переменного тока за половину периода, то после интегрирования мы получим следующее выражение для действующего значения тока (аналогично определяются действующие значения ЭДС и напряжения)
Векторное изображение гармонических функций
Если гармоническую функцию изобразить в виде вектора с длинной, равной его амплитуде, и вращать этот вектор против часовой стрелки с постоянной угловой скоростью w то в любой момент времени проекция этого вектора на вертикальную ось OY будет равна мгновенному значению этой гармонической функции.
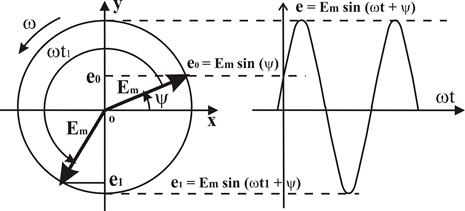
Векторное представление позволяет избавиться от проблем, связанных со сложением гармонических функций с различными амплитудами, и перейти к их векторному суммированию. Естественно, что при этом приходится учитывать их взаимную ориентацию, но это один из наиболее простых и наглядных способов расчета цепей переменного тока.
Из курса физики известно, что для мгновенных значений в цепях переменного тока справедливы все законы постоянного тока (Ома, Кирхгофа и т.д.). Эти же законы будут справедливы и для амплитудных и действующих значений при условии векторного сложения входящих в них величин.
Цепь переменного тока с активным сопротивлением
|
i = Im sin (ωt)
uR =? φR =?
u = iR = RIm sin ωt = Um sin ωt
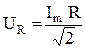=> UR = I R
Закон Ома для действующих значений 
|
i = Im sin (ωt)
uR = UmR sin ωt
На активном сопротивлении напряжение и ток совпадают по фазе, т. е. угол сдвига фаз между током и напряжением jR = 0