Синусоидальные токи и ЭДС сравнительно низких частот, до нескольких килогерц, получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых и полупроводниковых генераторов, подробно рассматриваемых в разделе – электроника.
13. Пассивные элементы электрической цепи. Резистор  , индуктивность
, индуктивность  и емкость
и емкость 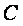 являются пассивными элементами электрической цепи. Резистор
являются пассивными элементами электрической цепи. Резистор  или активное сопротивление цепи – это элемент, в котором происходит рассеивание энергии в виде тепла или превращение электрической энергии в другой вид энергии: в световую, химическую или механическую.
или активное сопротивление цепи – это элемент, в котором происходит рассеивание энергии в виде тепла или превращение электрической энергии в другой вид энергии: в световую, химическую или механическую.
Индуктивность  и емкость
и емкость 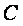 называются реактивными элементами цепи, в них происходят накапливание энергии в виде магнитного или электрического поля. Рассеивание энергии в таких элементах отсутствует. Идеальные элементы
называются реактивными элементами цепи, в них происходят накапливание энергии в виде магнитного или электрического поля. Рассеивание энергии в таких элементах отсутствует. Идеальные элементы  ,
,  ,
, 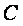 на схеме обозначаются так, как это показано на рис. 2.3а.
на схеме обозначаются так, как это показано на рис. 2.3а.

Реальные катушки индуктивности и конденсаторы рассеивают часть энергии. Этот факт учитывается с помощью добавочных сопротивлений  для катушки и
для катушки и  для конденсаторов, рис. 2.3б. В проволочных сопротивлениях и катушках индуктивности учитывают также межвитковую емкость
для конденсаторов, рис. 2.3б. В проволочных сопротивлениях и катушках индуктивности учитывают также межвитковую емкость  , рис. 2.3б; в реальном конденсаторе можно учесть паразитную индуктивность подводящих контактов
, рис. 2.3б; в реальном конденсаторе можно учесть паразитную индуктивность подводящих контактов  , рис. 2.3б.
, рис. 2.3б.
Индуктивный элемент в цепи синусоидального тока.
Индуктивный элемент учитывает явления накапливания энергии магнитного поля и характеризуется зависимостью потокосцепления  от тока
от тока  :
:
 , измеряется в генри (Гн).
, измеряется в генри (Гн).
Емкостный элемент в цепи синусоидального тока.
Емкость отражает явление накапливания энергии электрического поля и характеризуется зависимостью заряда  от напряжения
от напряжения  :
: 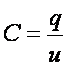
Резистивный элемент характеризует необратимые процессы преобразования электрической энергии в другие виды энергии. Для мгновенных значений тока через резистивный элемент справедлив закон Ома:
 , (2.1)
, (2.1)
т.е. кривые напряжения и тока резистивного элемента подобны. Мгновенная мощность резистивного элемента не зависит от знака тока и всегда положительна:
 . (2.2)
. (2.2)
16 Способы представления синусоидальных величин. Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат. Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1 и е2 соответствуют уравнения:

 .
.

Значения аргументов синусоидальных функций  и
и  называются фазами синусоид, а значение фазы в начальный момент времени (t=0):
называются фазами синусоид, а значение фазы в начальный момент времени (t=0):  и
и  - начальной фазой (
- начальной фазой (
 ).
).
Величину  , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на
, характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на  рад., то угловая частота есть
рад., то угловая частота есть  , где f– частота.
, где f– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
Для синусоидальных ЭДС е1 и е2 угол сдвига фаз:
 .
.
Векторное изображение синусоидально
изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами.При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
 
|
Пусть, например, в точке разветвления цепи (рис. 5) общий ток  равен сумме токов
равен сумме токов  и
и  двух ветвей:
двух ветвей:
 .
.
Каждый из этих токов синусоидален и может быть представлен уравнением
 и
и  .
.
Результирующий ток также будет синусоидален:
 .
.
Определение амплитуды  и начальной фазы
и начальной фазы  этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число
этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число  синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным
синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным  .
.
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
 .
.
Построение векторной диаграммы в масштабе позволяет определить значения  и
и  из диаграммы, после чего может быть записано решение для мгновенного значения
из диаграммы, после чего может быть записано решение для мгновенного значения  путем формального учета угловой частоты:
путем формального учета угловой частоты:  .
.
Представление синусоидальных ЭДС, напряжений
и токов комплексными числами
Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.
 Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в:
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в:
показательной 
тригонометрической  или
или
алгебраической  - формах.
- формах.
Например, ЭДС  , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
, изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
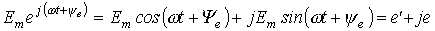 .
.
Фазовый угол  определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
 .
.
В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
 , ,
| (4) |
Комплексное число  удобно представить в виде произведения двух комплексных чисел:
удобно представить в виде произведения двух комплексных чисел:
 , ,
| (5) |
Параметр  , соответствующий положению вектора для t=0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой:
, соответствующий положению вектора для t=0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой:  , а параметр
, а параметр  - комплексом мгновенного значения.
- комплексом мгновенного значения.
Параметр  является оператором поворота вектора на угол wt относительно начального положения вектора.
является оператором поворота вектора на угол wt относительно начального положения вектора.
Вообще говоря, умножение вектора на оператор поворота  есть его поворот относительно первоначального положения на угол ±a.
есть его поворот относительно первоначального положения на угол ±a.
Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды  и оператора поворота
и оператора поворота  :
:
 .
.
Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
 , ,
| (6) |
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:
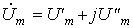 ,
,
- то для записи ее в показательной форме, необходимо найти начальную фазу  , т.е. угол, который образует вектор
, т.е. угол, который образует вектор  с положительной полуосью +1:
с положительной полуосью +1:
 .
.
Тогда мгновенное значение напряжения:
 ,
,
где  .
.
При записи выражения для определенности было принято, что  , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если
, т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если  , то при
, то при  (второй квадрант)
(второй квадрант)
, 
| (7) |
а при  (третий квадрант)
(третий квадрант)

| (8) |
или

| (9) |
Если задано мгновенное значение тока в виде 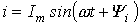 , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
, то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
 .
.
Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.
Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока  по рис. 5 получим:
по рис. 5 получим:

где  ;
;
 .
.
17. Комплексный метод расчета цепей синусоидального тока. Понятия комплексных токов и напряжений  ,
,  , комплексных сопротивлений и проводимостей Z и Y лежат в основе комплексного метода расчета цепей синусоидального тока.
, комплексных сопротивлений и проводимостей Z и Y лежат в основе комплексного метода расчета цепей синусоидального тока.
Для расчета цепи необходимо перейти от заданных характеристик действующих в цепи источников ЭДС и тока, используя формулы прямого преобразования (7.1), к их комплексным изображениям:  ;
;  (
( ,
,  — действующие ЭДС и токи, e, J — их начальные фазы). При наличии единственного источника его начальную фазу можно принять равной нулю, тогда его комплексное изображение будет вещественным. Далее вводятся комплексные сопротивления (или проводимости) элементов цепи: ZR = R; ZL = j L; ZC = 1/ j C или YR = 1/ R; YL = 1/ j L; YC = j C. Эти величины выражают связи комплексных токов
— действующие ЭДС и токи, e, J — их начальные фазы). При наличии единственного источника его начальную фазу можно принять равной нулю, тогда его комплексное изображение будет вещественным. Далее вводятся комплексные сопротивления (или проводимости) элементов цепи: ZR = R; ZL = j L; ZC = 1/ j C или YR = 1/ R; YL = 1/ j L; YC = j C. Эти величины выражают связи комплексных токов  и напряжений
и напряжений  на элементах цепи:
на элементах цепи:  (
(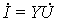 ). Сами комплексные токи и напряжения подчиняются законам Кирхгофа:
). Сами комплексные токи и напряжения подчиняются законам Кирхгофа:  ;
; 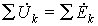 . Поэтому далее комплексные величины рассчитываются на основе уравнений Кирхгофа либо вытекающих из них узловых или контурных уравнений. При этом матрицы узловых проводимостей Y у или контурных сопротивлений Z к, формируемые из комплексных проводимостей или сопротивлений элементов цепи, имеют комплексные элементы.
. Поэтому далее комплексные величины рассчитываются на основе уравнений Кирхгофа либо вытекающих из них узловых или контурных уравнений. При этом матрицы узловых проводимостей Y у или контурных сопротивлений Z к, формируемые из комплексных проводимостей или сопротивлений элементов цепи, имеют комплексные элементы.
К комплексным величинам  и
и  можно применять принципы наложения и взаимности. Комплексные сопротивления Z и проводимости Y подчиняются правилам суммирования и преобразования при последовательном и параллельном соединениях, тождественным правилам преобразованиям сопротивлений R и проводимостей G резистивных элементов.
можно применять принципы наложения и взаимности. Комплексные сопротивления Z и проводимости Y подчиняются правилам суммирования и преобразования при последовательном и параллельном соединениях, тождественным правилам преобразованиям сопротивлений R и проводимостей G резистивных элементов.
Таким образом, комплексный метод позволяет распространить на расчет цепей синусоидального тока все известные способы и методы расчета резистивных цепей. Их соответствие расчетным величинам и формулам комплексного метода показано в Tабл. 7.2.
Значения комплексных токов  и напряжений
и напряжений  определяют действующие значения как модуль соответствующей комплексной величины (или его амплитуду, если при анализе используются комплексные амплитуды). Начальная фаза равна аргументу соответствующей комплексной величины. Таким образом, для перехода от комплексных изображений
определяют действующие значения как модуль соответствующей комплексной величины (или его амплитуду, если при анализе используются комплексные амплитуды). Начальная фаза равна аргументу соответствующей комплексной величины. Таким образом, для перехода от комплексных изображений  и
и  к представлению искомых величин во временной области i (t) и u (t) используются формулы обратного преобразования (7.2).
к представлению искомых величин во временной области i (t) и u (t) используются формулы обратного преобразования (7.2).
Таблица 7.2.