df.1 Пусть 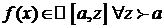 , несобственный интеграл
, несобственный интеграл
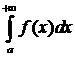 (1)
(1)
называется абсолютно сходящимся, если сходится несобственный интеграл
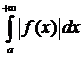 (2)
(2)
Если интеграл (1) сходится, а интеграл (2) расходится, то (1) называется условно сходящимся.
Аналогичные определения можно дать для других типов Н.И.
df.2 Пусть 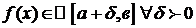 . Н. И.
. Н. И. 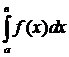 называется абсолютно сходящимся, если сходится Н. И.
называется абсолютно сходящимся, если сходится Н. И. 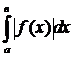 .
.
Th.6 О сходимости абсолютно сходящегося Н. И.
Пусть 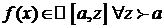 (или
(или 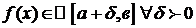 ) и Н. И.
) и Н. И. 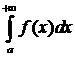 (или
(или 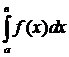 ) сходятся абсолютно. Тогда этот интеграл сходится.
) сходятся абсолютно. Тогда этот интеграл сходится.
Доказательство:
Пусть, например, 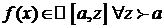 (случай
(случай 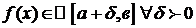 рассмотреть самостоятельно) и Н. И.
рассмотреть самостоятельно) и Н. И. 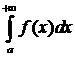 сходится абсолютно. По условию
сходится абсолютно. По условию 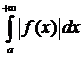 - сходится (по Критерию Коши)
- сходится (по Критерию Коши) 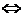

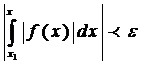 . Из оценки для
. Из оценки для 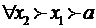 :
: 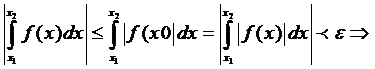 выполняется
выполняется
Критерий Коши. А это значит 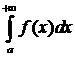 - сходится.
- сходится.
Th.7 Признак Дирихле.
Пусть 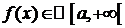 , а
, а 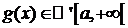 и выполняются следующие условия:
и выполняются следующие условия:
а) функция 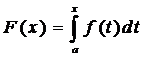 (первообразная для f),
(первообразная для f),
ограничена на 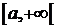 (1), т.е.
(1), т.е. 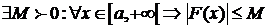 .
.
б) функция 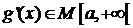 - монотонна, не меняет знака на
- монотонна, не меняет знака на 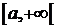 ,
,
т.е. 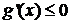 (2)
(2)
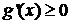 (3)
(3)
с) 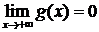 (4)
(4)
Тогда интеграл 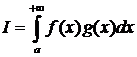 (5) – сходится.
(5) – сходится.
Доказательство:
Покажем, что функция f ·g – удовлетворяет на 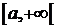 условию Коши: т.е.
условию Коши: т.е.
 .
.
Согласно формуле интегрирования по частям для 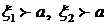 получаем
получаем
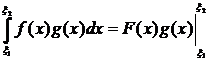 -
- 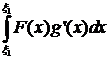 (6)
(6)
Из условия (1) 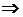 , что
, что 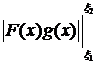
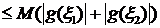 (7)
(7)
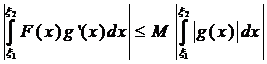 (8)
(8)
Заметим, что 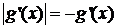 - если выполнено условие (2) и
- если выполнено условие (2) и 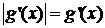 - если выполнено условие (3).
- если выполнено условие (3).
Поэтому для первого случая:
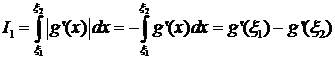
а во втором случае: 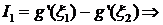
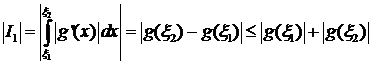 (9)
(9)
Поэтому из равенства (6), используя оценки (7) и (9), получаем неравенство:
 (10)
(10)
Согласно условию (4), что 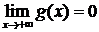 :
: 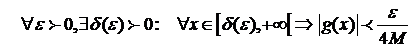 (11)
(11)
Поэтому для 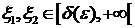 из (10) и (11) следует, что
из (10) и (11) следует, что 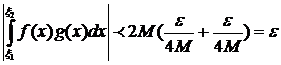 , т.е. функция f ·g удовлетворяет на
, т.е. функция f ·g удовлетворяет на 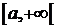 условию Коши и по Th. для сходимости Н. И.
условию Коши и по Th. для сходимости Н. И. 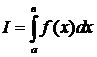
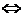 чтобы выполнялось условие Коши, т.е.
чтобы выполнялось условие Коши, т.е. 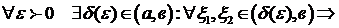
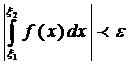 . Следовательно, наш Н. И. (5) – сходится.
. Следовательно, наш Н. И. (5) – сходится.
Следствие. (Признак Абеля)
Если а) 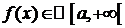 ;
;
б) 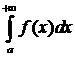 - сходится;
- сходится;
в) 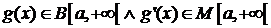 (т. е. выполняются условия ограниченности и монотонности (2) и (3) Th.7).
(т. е. выполняются условия ограниченности и монотонности (2) и (3) Th.7).
То интеграл 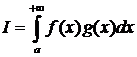 - сходится.
- сходится.
Доказательство:
По Th. о пределе монотонной функции существует конечный предел
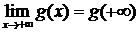 , и поэтому функция
, и поэтому функция 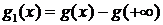 - монотонно стремится к нулю при
- монотонно стремится к нулю при 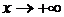 . Из условия б)
. Из условия б) 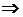 , что f имеет ограниченную первообразную
, что f имеет ограниченную первообразную 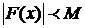 . По Th.7 интеграл от функции
. По Th.7 интеграл от функции 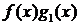 на
на 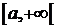 сходится. Т.к.
сходится. Т.к.  , то интеграл
, то интеграл
 - сходится.
- сходится.
Замечание.
Признаки Дирихле и Абеля являются достаточными. Поэтому, если их условия не выполняются, то ничего нельзя сказать о сходимости интеграла.
§ 10.4 ГЛАВНОЕ ЗНАЧЕНИЕ РАСХОДЯЩЕГОСЯ НЕСОБСТВЕННОГО ИНТЕГРАЛА
Пусть 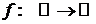 и
и 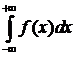 - расходится.
- расходится.
df.1 Пусть f(x) интегрируема по Риману на любом конечном отрезке 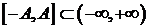 . Тогда главным значением интеграла
. Тогда главным значением интеграла 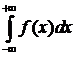 называют конечный предел
называют конечный предел 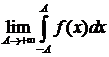 и обозначают:
и обозначают:
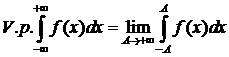
(V.p. – начальные буквы французских слов valeur principal – главное значение).
Определенное таким образом главное значение отличается от определения несобственного интеграла 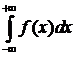 тем, что в последнем
тем, что в последнем 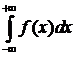 =
= 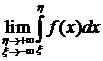 , переменные
, переменные 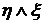 независимо друг от друга стремятся к
независимо друг от друга стремятся к 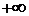 и
и 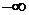 , соответственно.
, соответственно.
Очевидно, что в случае сходимости Н. И. его главное значение тем более существует и совпадает с ним. Поэтому главное значение имеет смысл рассматривать для расходящихся интегралов.
df.2 Пусть 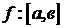 \
\ 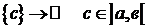 .
. 
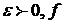 - неограниченная в (.) c.
- неограниченная в (.) c.
Тогда главным значением Н. И. 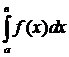 называют конечный предел
называют конечный предел
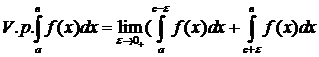
Для практического использования признаков сходимости необходимо иметь «эталонные» интегралы, т.е. интегралы, о сходимости которых известно.
ПРИМЕРЫ.
№1. 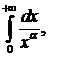 Найти при каких
Найти при каких  он сходится и при каких
он сходится и при каких  расходится.
расходится.
Решение:
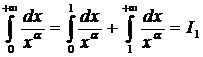 ·
· 
А) Исследуем  на сходимость. Применим
на сходимость. Применим  =
=
= 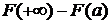 понимая, что
понимая, что  .
.
Пусть  , тогда:
, тогда:
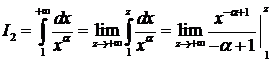 =
= 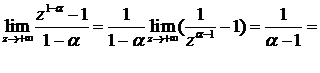
 , если
, если 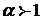 .
.
= 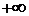 , если
, если 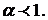
Первый ответ получен так: если 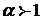 , то
, то  и если
и если 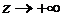 , то
, то
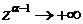 , а дробь
, а дробь 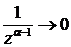 .
.
Второй ответ объясняется так: если  , то
, то 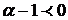 , а
, а 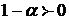 . Тогда
. Тогда
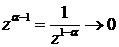 , когда
, когда 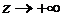 , т.е. величина
, т.е. величина 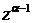 - бесконечно малая. Поэтому величина
- бесконечно малая. Поэтому величина 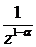 , которая нас интересует, - величина бесконечно большая.
, которая нас интересует, - величина бесконечно большая.
Осталось рассмотреть случай 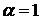 :
:

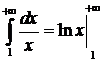 =
= 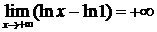 , следовательно
, следовательно 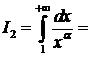
 , если
, если 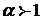 , интеграл сходится.
, интеграл сходится.
= 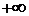 , если
, если 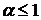 , интеграл расходится.
, интеграл расходится.
Исследуем на сходимость интеграл 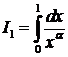 . Особенность интеграла в том, что при
. Особенность интеграла в том, что при  функция неопределенна в левом конце промежутка в (.) О и стремится к бесконечности при
функция неопределенна в левом конце промежутка в (.) О и стремится к бесконечности при 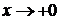 .
.
Применив формулу Ньютона – Лейбница, получим:
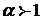
 =
= 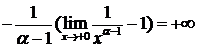 , т.к.
, т.к.  .
.
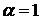
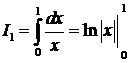 =
= 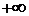

 =
= 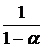
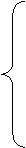
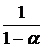 , если, интеграл сходится.
, если, интеграл сходится.
Т. о. 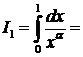
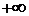 , если
, если  , интеграл расходится.
, интеграл расходится.
№2. Исследуем на сходимость интеграл: 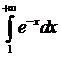 .
.
Решение:
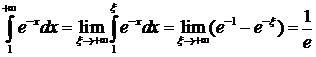 - сходится.
- сходится.
№3. Исследуем на сходимость интегралы:
I. 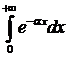 II.
II. 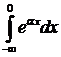
 Решение:
Решение: 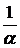 , если
, если 
Интеграл 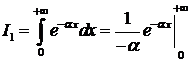 =
= 
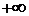 , если
, если 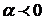
При 
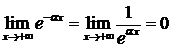 , т.к.
, т.к. 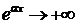 при
при 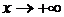 , а при
, а при 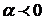
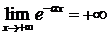 .
.
Заключение:

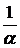 , при
, при  - сходится
- сходится
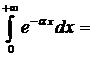
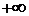 , при
, при 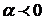 - расходится.
- расходится.
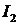 =
= 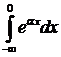 сводится к первому интегралу подстановкой:
сводится к первому интегралу подстановкой:
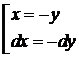

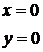

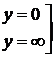 (Доказать самостоятельно).
(Доказать самостоятельно).
№4. А) 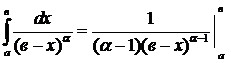 =
=
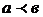 Пусть
Пусть  .
.
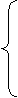 сходится,
сходится,  , т.к.
, т.к. 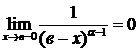
=
расходится, 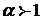 , т.к.
, т.к. 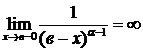
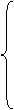 Пусть
Пусть 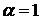 .
. 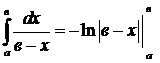 - расходится, т.к.
- расходится, т.к. 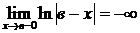 .
.
сходится,  .
.
Т. о. 
расходится,  .
.
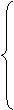
сходится,  .
.
В) 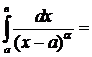
расходится,  .
.
Аналогично А. Сделать самостоятельно.
№5. Исследовать на сходимость: 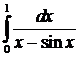
Решение:
 = (правило Лопиталя) =
= (правило Лопиталя) = 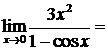
= 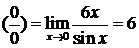 .
.
Т.к. 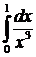 расходится, то наш интеграл также расходится.
расходится, то наш интеграл также расходится.
№6. Исследовать на сходимость:  .
.
Решение:
 =
= 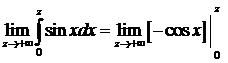 =
= 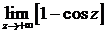 этот предел не стремится ни к какому пределу, следовательно, интеграл расходится.
этот предел не стремится ни к какому пределу, следовательно, интеграл расходится.
Замечание.
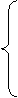 если
если 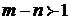 , интеграл сходится.
, интеграл сходится.
Если интеграл 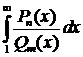 =
=
если 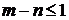 , интеграл расходится.
, интеграл расходится.
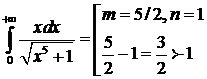
 - интеграл сходится.
- интеграл сходится.
№7. Исследовать на сходимость интеграл: 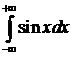 .
.
Решение: Очевидно, что интеграл расходится, т.к. не существует ни 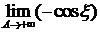 , ни
, ни 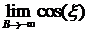 .
.
Главное значение существует:
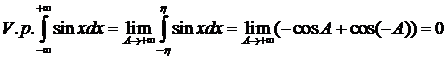
№8. Найти главное значение 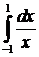 .
.
Решение:
Н. И. 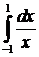 как мы видели выше, не существует. Тем не менее у него есть главное значение:
как мы видели выше, не существует. Тем не менее у него есть главное значение:
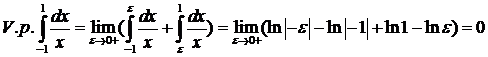
Здесь с=0.
Главное значение есть, а интеграл 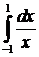 не существует.
не существует.
№9. Вычислить интеграл 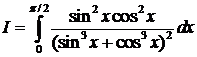 .
.
Решение:
Положим 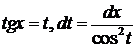 .
. 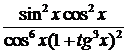 .
.
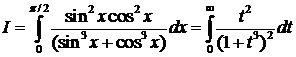 . Мы получили несобственный интеграл, который легко вычисляется следующим образом:
. Мы получили несобственный интеграл, который легко вычисляется следующим образом:
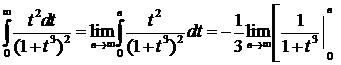
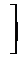 =
= 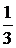 .
.
№10. Вычислить несобственный интеграл: 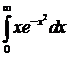 .
.
Решение:
Подынтегральная функция определена и непрерывна при всех значениях «x» и, следовательно, имеем первообразную:
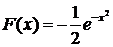
По определению имеем:
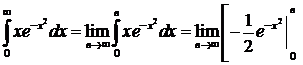
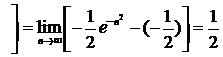 .
.
№11. Вычислить несобственный интеграл: 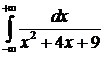 .
.
Оба предела интегрирования бесконечны, поэтому предварительно разобьем данный интеграл на два:
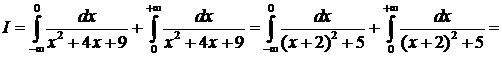 =
= 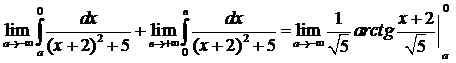 +
+
+ 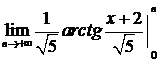 =
= 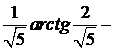
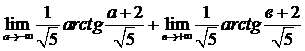 -
-
- 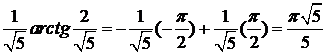 .
.
№12. Сходится ли несобственный интеграл:  .
.
Решение:
 =
= 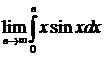 . Применяем правило интегрирования по частям, полагая:
. Применяем правило интегрирования по частям, полагая:
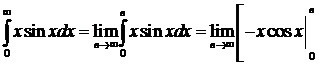
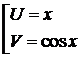

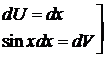 = +
= +
 =
= 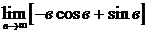 .
.
Этот предел не существует, следовательно, интеграл расходится.
№13. Вычислить несобственный интеграл: 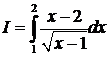 .
.
Решение:
Преобразуем интеграл следующим образом:
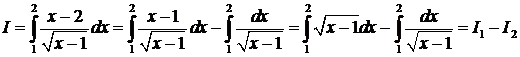
В интеграле 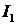 подынтегральная функция непрерывна на промежутке
подынтегральная функция непрерывна на промежутке  , поэтому его можно вычислить по формуле Ньютона – Лейбница:
, поэтому его можно вычислить по формуле Ньютона – Лейбница:
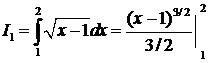 =
= 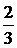
Интеграл 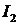 - несобственный, т.к подынтегральная функция
- несобственный, т.к подынтегральная функция 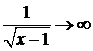
при 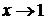 . По определению имеем:
. По определению имеем:
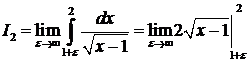 =
= 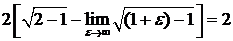 .
.
Окончательно 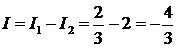 .
.
№14. Вычислить несобственный интеграл: 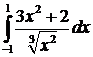 .
.
Решение:
Преобразуем:
 . Интеграл
. Интеграл 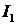 вычисляется по формуле Ньютона – Лейбница, т.к. подынтегральная функция непрерывна.
вычисляется по формуле Ньютона – Лейбница, т.к. подынтегральная функция непрерывна.
 =
=  . Интеграл
. Интеграл 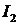 следует представить в виде суммы двух интегралов (ибо (.) разрыва x=0 лежит внутри промежутка интегрирования).
следует представить в виде суммы двух интегралов (ибо (.) разрыва x=0 лежит внутри промежутка интегрирования).

= 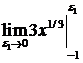 +
+ 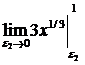 = 3+3 = 6.
= 3+3 = 6.
Итак, 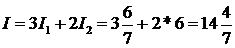 .
.
№15. Исследовать на сходимость: 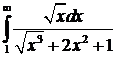 .
.
Решение:
Сравним подынтегральную функцию с 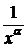 . Подберем
. Подберем 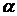 такое, чтобы
такое, чтобы  был конечен и отличен от «0».
был конечен и отличен от «0».
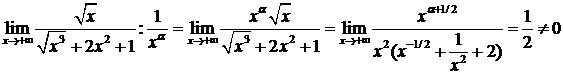
Если 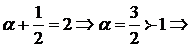 интеграл сходится.
интеграл сходится.
№16. Исследовать на сходимость: 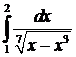 .
.
Решение:
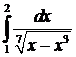 =
= 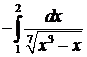 . x=1 - особая точка.
. x=1 - особая точка.
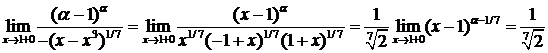
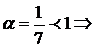 интеграл расходится.
интеграл расходится.
№17. Вычислить  .
.
Решение:
Согласно определению:
 =
= 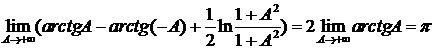 .
.
№18. Вычислить  .
.
Решение:
 =
= 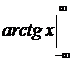 =
= 
Можно было бы вести записи так:
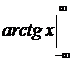 =
= 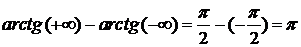 .
.
№19. Вычислить  .
.
Решение:
Знаменатель обращается в ноль в точках x=1 и x=2. Пусть 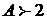 - любое фиксированное. По определению:
- любое фиксированное. По определению:
 =
=  +
+ 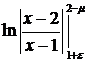 +
+ 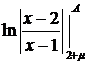
 +
+
+ 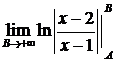 =
= 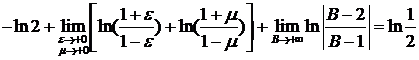 .
.
№20. Рассмотрим интеграл Дирихле: 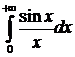 .
.
Решение:
Заметим, что в силу 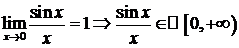 .
.
Поэтому 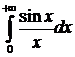 =
= 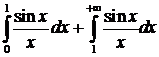 .
.
Положим 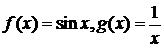 , тогда
, тогда 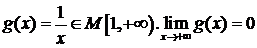 .
.
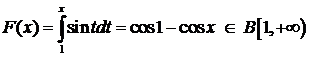
По признаку Дирихле Н. И. 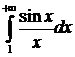 сходится, но тогда сходится и интеграл Дирихле.
сходится, но тогда сходится и интеграл Дирихле.

