(Интегрирование на некомпактном промежутке)
Ранее был рассмотрен определенный интеграл, необходимым условием существования которого являлось условие ограниченности подынтегральной функции на отрезке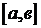 
(
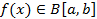).При этом подразумевалось, что отрезок интегрирования 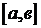конечный, или как его называют компактный. Такие интегралы в противоположность тем, которые будут рассматриваться в этом разделе, иногда, называют собственными.
df.1 Компактным промежутком будем называть 
-ой сегмент 
.
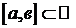df.2 Пусть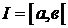 
- полуинтервал числовой прямой 
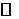, причем ” в ” может быть 
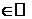, символами 
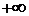, а функция 
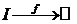интегрируема на 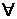сегменте 
.
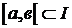df.3 Пусть f(x) – определена на промежутке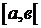 
и f(x)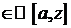 
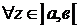, тогда предел
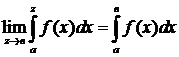(1)
называют несобственным интегралом от функции f(x) на промежутке 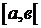, если этот предел 
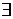и конечен.
Очевидно возможны 2 частных случая:
1) Интеграл с бесконечным верхним пределом:
, 
.
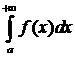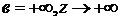2) Интеграл от неограниченной функции:
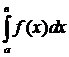, в=const в этом случае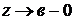 
Заметим, что если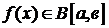 
(ограничена), тогда получаем обычный интеграл Римана. В силу непрерывности функции 
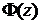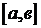на (т.е.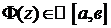 
), т.е.
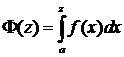
df.4 Пусть f(z) определена на промежутке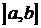 
. (
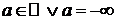) и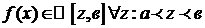 
. Тогда предел
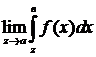(2)
называется несобственным интегралом от функции f(x) на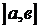 
, если предел 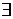и конечен.
Опять возможны два случая:
1) с бесконечным нижним пределом:
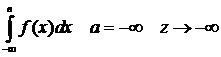
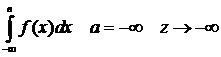
2) интеграл от неограниченной функции:
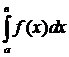
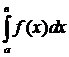, здесь 
.
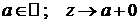df.5 Пусть f(x) определена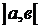 
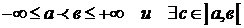, что 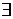-ют несобственные интегралы 
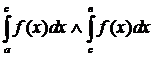, то по df: 
.
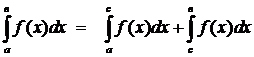df:
ЗАМЕЧАНИЕ. Можно показать, что в этом определении значение
н. и. не зависит от выбора (.) ”c”.
Заметим также, что последнее определение эквивалентно следующему определению:
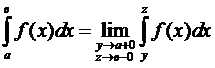df:
т.е. здесь рассматривается предел функции двух переменных ” y ”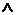 
” z ”. Т.е. при вычислении предела 
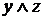стремятся к 
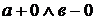независимо.
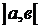df.6 f(x) определена на за исключением конечного числа точек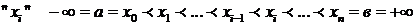 
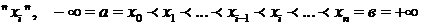и н.и. 
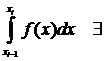-ет (i= 1,2,..., n). Тогда н. и. от f(x) на 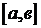назовем:
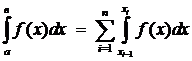df:
По определению полагаем геометрический смысл н. и. – площадь соответствующих «бесконечных» криволинейных трапеций.
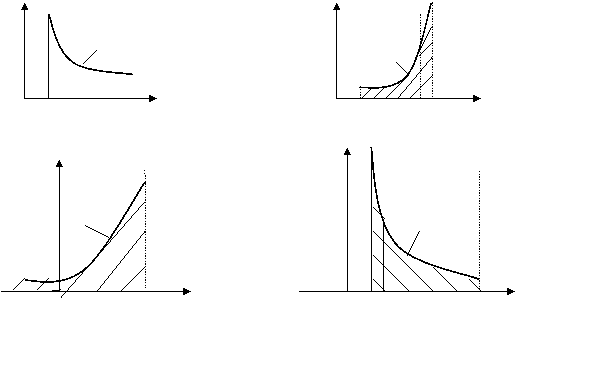y df.3 y df.3
f(x)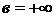 
f(x)–неограни
f(x) ченная вU(в)
0 a x 0 a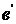 
в x
y y
df.4df.4
f(x) 
f(x) – неограни-
f(x) ченная в U(a)
0 в x 0 a’ a в x
y y
df.5 df.5
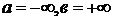f(x) f(x) неогра-
f(x) ниченная в
U(а) U(в)
0 x a 0 в x
Если соответствующие пределы в определениях 3, 4 5 -ют и конечны, то говорят, что функция f(x) интегрируема в несобственном смысле (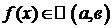
и т.д.), а интеграл – сходится. В противном случае интеграл – расходится.
Можно показать, что свойства интегралов из df. 3 4 аналогичны, а интегралы вида 5 6 сводятся к ним.
Поэтому в дальнейшем изложении в основном ограничимся несобственными интегралами типа (1), т.е. df. 3
§ 10.2 СВОЙСТВА НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ.
Многие из них (однако, не все) аналогичны свойствам определенного интеграла.
. Формула Ньютона – Лейбница.
Пусть f(x)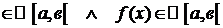 
и F(x) - первообразная f(x) на 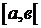, тогда:
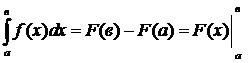
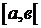
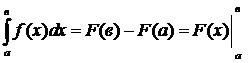
При этом под F(в) понимается:
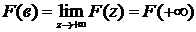
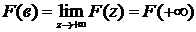или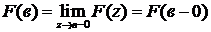 
Доказательство:
Т. к. 
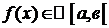, то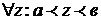 
по формуле Ньютона – Лейбница на 
:
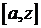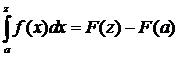
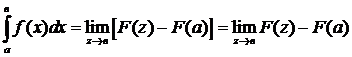
2 
. Линейность.
Пусть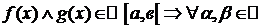 
: 
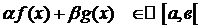и
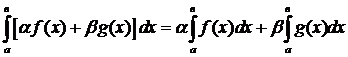(1)
Доказательство:
Из сходимости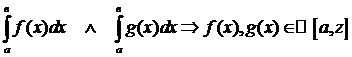 
: 
.
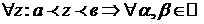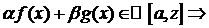
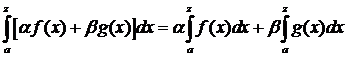Переходим в последнем равенстве к пределу пр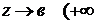и 
или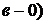 
, т.к. 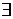пределы в правой части, то 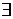пределы левой части 
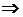равенство (1).
3 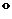. Интегрирование неравенств.
Пусть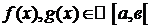 
и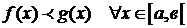 
, тогда 
.
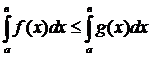4 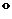. Интегрирование по частям.
Пусть:
1. 
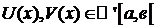
2. Пара из трех функций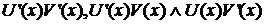 
интегрируема на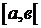 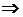интегрируема и третья пара и справедливо неравенство:
- 
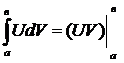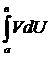(1)
При этом входящие в (1) выражения понимаются в несобственном смысле.
(Свойства 3 и 4 доказать самостоятельно).
5 . Замена переменной в Н. И.
Пусть:
1. .
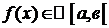2. 
.
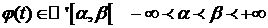3. 
, 
.
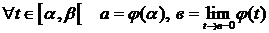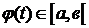Тогда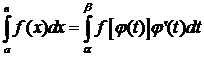 
, причем оба интеграла сходятся или расходятся одновременно. (Без доказательства).
Отметим, что, используя свойство 5, можно показать, что всегда от интеграла с бесконечным пределом можно перейти к интегралу от неограниченной функции и наоборот.
Пусть, например,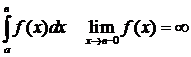 
. Сделаем замену 
;
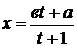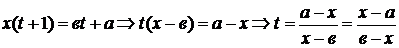
при x=a, t=0;
при x=в-0, t= ;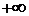
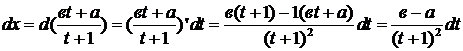
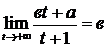, тогда 
.
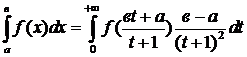Поэтому далее в основном будем рассматривать интегралы вида:
.
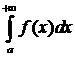6 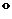. Аддитивность Н. И.
(от латинского additivus – прибавляемый, свойство величин).
Пусть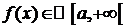 
, тогда 
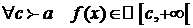и 
.
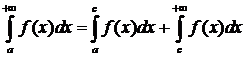Доказательство:
Пусть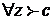 
: 
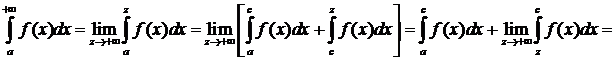
=(предел слева 
предел справа) = 
.
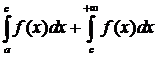§ 10.3 ПРИЗНАКИ СХОДИМОСТИ Н. И.
Будем рассматривать интегралы вида: 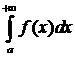. Обозначим 
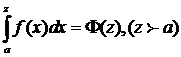и назовем его частным интегралом, а 
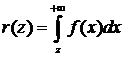- остатком.
Th.1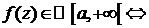 
1) 
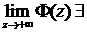и конечен.
2) 
.
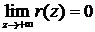Причем условия 1 и 2 эквивалентны.
Доказательство:
Условие 1 следует из определения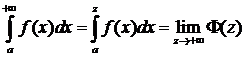 
. В силу аддитивности:
.
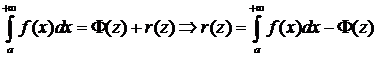Переходя к пределу при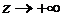 
получим .
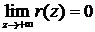Следствие.
Очевидно, что 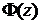- первообразная для функции f(x) на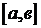 
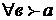, т.о. 
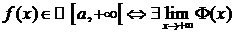, что также из обобщения формулы Ньютона – Лейбница.
Следовательно, простейшим способом установления сходимости несобственного интеграла является вычисление его по формуле Ньютона – Лейбница:
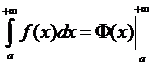
Однако, не всегда возможно найти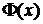 
или нахождение ее громоздко.
В этом случае используются признаки сходимости, о которых будет идти речь ниже.
Th.2 Критерий Коши.
.
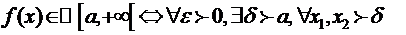
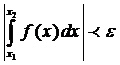Доказательство:
В силу Th.1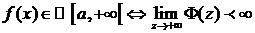 
, но по критерию Коши существования конечного предела 
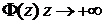(смотри I семестр): 
: 
.
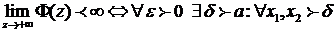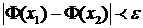(Необходимо полагать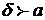 
, т.к. 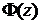ограничена на 
).
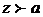Но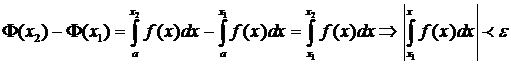 
.
●Достаточно эффективных при практическом использовании признаков (теорем) сходимости н.и. от произвольных функций не существует. Поэтому далее ограничимся только случаем неотрицательных функций, т.е.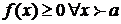 
.
Отметим при это, что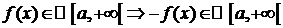 
по свойству линейности.
Т.о. все результаты, полученные для неотрицательных функций могут быть перенесены на неположительные функции (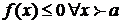
) с небольшими изменениями.
Th.3 Необходимое и достаточное условия сходимости для