Система (от греч. σύστημα, «составленный») — множество взаимосвязанных объектов и ресурсов, организованных процессом системогенеза в единое целое и противопоставляемое среде.
Термодинамическая система — это любая область пространства, ограниченная действительными или воображаемыми границами, выбранными для анализа её внутренних термодинамических параметров.
Пространство, смежное с границей системы, называется внешней средой. У всех термодинамических систем есть среда, с которой может происходить обмен энергии и вещества.
Границы термодинамической системы могут быть неподвижными или подвижными.
Системы могут быть большими или маленькими, в зависимости от границ. Например, система может охватывать всю холодильную систему или газ в одном из цилиндров компрессора.
Система может существовать в вакууме или может содержать несколько фаз одного или более веществ. Термодинамические системы могут содержать сухой воздух и водяной пар (два вещества) или воду и водяной пар (две стадии одного и того же вещества). Однородная система состоит из одного вещества, одной его фазы или однородной смеси нескольких компонентов.
Системы бывают замкнутыми или открытыми. В замкнутой системе не происходит никаких обменных процессов со средой.
В открытой системе и энергия и вещество могут переходить из системы в среду и обратно. При анализе насосов и теплообменников необходима открытая система, так как жидкости должны пересекать границы при анализе. Если массовый расход открытой системы устойчивый и однородный, систему называют открытой системой с постоянным расходом.
Состояние термодинамической системы определяется физическими свойствами вещества. Температура, давление, объем, внутренняя энергия, энтальпия и энтропия — это термодинамические величины, определяющие те или иные интегральные параметры системы. Данные параметры строго определяются лишь для систем, находящихся в состоянии термодинамического равновесия.
Параметры состояния, термодинамические параметры, физические величины, характеризующие состояние термодинамической системы (например, температура, давление, удельный объём, намагниченность, электрическая поляризация и др.). Различают экстенсивные параметры состояния, пропорциональные массе термодинамической системы, и интенсивные параметры состояния, не зависящие от массы системы. К экстенсивным Параметры состояния относятся: объём, внутренняя энергия, энтропия, энтальпия, изохорно-изотермический потенциал (гиббсова энергия), изобарно-изометрический потенциал (гельмгольцева энергия); к интенсивным параметрам состояния— давление, температура, концентрация, магнитная индукция и др. Параметры состояния взаимосвязаны, так что равновесное состояние системы можно однозначно определить, установив значения ограниченного их числа.
Для понимания второго начала термодинамики очень большое значение имеет правильное представление об обратимых и необратимых процессах. Представим себе замкнутую материальную систему т.е, такую, которая сохраняет постоянное количество вещества, но может взаимодействовать с внешней средой или посредством процессов теплопередачи, или совершая работу. Такую систему можно назвать изолированной в материальном отношении или закрытой. Какие бы процессы в такой системе ни протекали, мы всегда можем вернуть ее в исходное состояние, воздействуя на нее извне. Например, если в системе происходит (при Т = const) смешение газообразного водорода с углекислым газом, то образовавшуюся смесь можно разделить на исходные вещества путем глубокого охлаждения, а потом нагреть отделенные друг от друга водород и углекислый газ до начальной температуры. Таким образом, в системе все вернется в исходное состояние, и в этом смысле можно было бы считать все процессы, протекавшие в системе, обратимыми. Однако в этом суммарном процессе, кроме системы, принимали участие и тела, находящиеся во внешней среде, которые также меняли свое состояние.
Если в системе происходит процесс, после которого можно систему каким-либо способом вернуть в исходное состояние так, что все внешние тела, принимавшие участие в первоначальном процессе и в возвращении системы в исходное состояние, также придут в исходное состояние, то такой процесс называется обратимым. Если же невозможно найти способ вернуть и систему, и внешние тела в исходное состояние, то процесс называется необратимым. Следовательно, необратимым является процесс, вызывающий такие изменения в природе, устранение которых неизбежно влечет за собой другие неустранимые изменения.
Принципиальная возможность обратимых процессов не вызывает сомнения. Например, обратимы все чисто механические процессы (качание маятника без трения, колебание притягивающихся и отталкивающихся тел и т. п.).
Второе начало термодинамики утверждает, что в природе существуют и необратимые процессы, примером которых может служить расширение газа в пустоту или передача энергии от одного тела к другому при конечной разности температур этих тел.
Обратимые процессы представляют известную идеализацию реально происходящих процессов. Например, процессы теплопередачи могут происходить обратимо лишь тогда, когда разность температур между телом, передающим энергию ("нагревателем") и телом, получающим энергию ("холодильником") бесконечно мала (в пределе равна нулю). Работа сжатия тела может совершаться обратимо тогда, когда давление внешней среды на тело и давление тела на внешнюю среду бесконечно мало отличаются друг от друга (в пределе одинаковы). Эти примеры показывают, что процессы тогда протекают обратимо, когда они происходят в условиях равновесия. Следовательно, они идут бесконечно медленно. Тем не менее, в классической термодинамике эти процессы играют очень важную роль, так как они показывают принципиальную возможность перевести систему из одного состояния в другое обратимым путем, а время не входит в число параметров термодинамики (классической). В тех случаях, когда в эксперименте (например, при определении электродвижущей силы гальванического элемента) требуется производить измерения в условиях обратимости протекания процесса, это делается с известным приближением, удовлетворяющим достижению необходимой точности.
В общем случае направление и предел самопроизвольного протекания процесса в любых системах определяет принцип минимума свободной энергии:
Самопроизвольно могут протекать только те процессы, которые приводят к понижению свободной энергии системы; система приходит в состояние равновесия, когда свободная энергия достигает минимального значения.
Для закрытых систем, находящихся в изобарно-изотермических либо изохорно-изотермических условиях свободная энергия принимает вид изобарно-изотермического либо изохорно-изотермического потенциалов (т.н. свободная энергия Гиббса и Гельмгольца соответственно). Данные функции называют иногда просто термодинамическими потенциалами, что не вполне строго, поскольку термодинамическими потенциалами являются также внутренняя энергия (изохорно-изэнтропный) и энтальпия (изобарно-изэнтропный потенциал).
Протекание самопроизвольного процесса в закрытой системе сопровождается уменьшением свободной энергии системы (dG < 0, dF < 0). Очевидно, что рано или поздно (напомним, что понятие "время" в термодинамике отсутствует) система достигнет минимума свободной энергии. Условием минимума некоторой функции Y = f(x) является равенство нулю первой производной и положительный знак второй производной: dY = 0; d2Y > 0. Таким образом, условием термодинамического равновесия в закрытой системе является минимальное значение соответствующего термодинамического потенциала:
Изобарно-изотермические (P = const, T = const):
ΔG = 0 dG = 0, d2G > 0
Изохорно-изотермические (V = const, T = const):
ΔF = 0 dF = 0, d2F > 0
Состояние системы с минимальной свободной энергией есть состояние термодинамического равновесия:
Термодинамическим равновесием называется такое термодинамическое состояние системы, которое при постоянстве внешних условий не изменяется во времени, причем эта неизменяемость не обусловлена каким-либо внешним процессом.
Учение о равновесных состояниях – один из разделов термодинамики. Далее мы будем рассматривать частный случай термодинамического равновесного состояния – химическое равновесие. Как известно, многие химические реакции являются обратимыми, т.е. могут одновременно протекать в обоих направлениях – прямом и обратном. Если проводить обратимую реакцию в закрытой системе, то через некоторое время система придет в состояние химического равновесия – концентрации всех реагирующих веществ перестанут изменяться во времени.
Необходимо отметить, что достижение системой состояния равновесия не означает прекращения процесса; химическое равновесие является динамическим, т.е. соответствует одновременному протеканию процесса в противоположных направлениях с одинаковой скоростью.
Химическое равновесие является подвижным – всякое бесконечно малое внешнее воздействие на равновесную систему вызывает бесконечно малое изменение состояния системы; по прекращении внешнего воздействия система возвращается в исходное состояние. Ещё одним важным свойством химического равновесия является то, что система может самопроизвольно прийти в состояние равновесия с двух противоположных сторон. Иначе говоря, любое состояние, смежное с равновесным, является менее устойчивым, и переход в него из состояния равновесия всегда связан с необходимостью затраты работы извне.
Энергия – мера способности системы совершать работу; общая качественная мера движения и взаимодействия материи. Энергия является неотъемлемым свойством материи. Различают потенциальную энергию, обусловленную положением тела в поле некоторых сил, и кинетическую энергию, обусловленную изменением положения тела в пространстве.
Внутренняя энергия системы – сумма кинетической и потенциальной энергии всех частиц, составляющих систему. Можно также определить внутреннюю энергию системы как её полную энергию за вычетом кинетической и потенциальной энергии системы как целого.
Формы перехода энергии от одной системы к другой могут быть разбиты на две группы. В первую группу входит только одна форма перехода движения путем хаотических столкновений молекул двух соприкасающихся тел, т.е. путём теплопроводности (и одновременно путём излучения). Мерой передаваемого таким способом движения является теплота. Теплота есть форма передачи энергии путём неупорядоченного движения молекул. Во вторую группу включаются различные формы перехода движения, общей чертой которых является перемещение масс, охватывающих очень большие числа молекул (т.е. макроскопических масс), под действием каких-либо сил. Таковы поднятие тел в поле тяготения, переход некоторого количества электричества от большего электростатического потенциала к меньшему, расширение газа, находящегося под давлением и др. Общей мерой передаваемого такими способами движения является работа – форма передачи энергии путём упорядоченного движения частиц.
Теплота и работа характеризуют качественно и количественно две различные формы передачи движения от данной части материального мира к другой. Теплота и работа не могут содержаться в теле. Теплота и работа возникают только тогда, когда возникает процесс, и характеризуют только процесс. В статических условиях теплота и работа не существуют. Различие между теплотой и работой, принимаемое термодинамикой как исходное положение, и противопоставление теплоты работе имеет смысл только для тел, состоящих из множества молекул, т.к. для одной молекулы или для совокупности немногих молекул понятия теплоты и работы теряют смысл. Поэтому термодинамика рассматривает лишь тела, состоящие из большого числа молекул, т.е. так называемые макроскопические системы.
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Первое начало термодинамики является постулатом – оно не может быть доказано логическим путем или выведено из каких-либо более общих положений. Истинность этого постулата подтверждается тем, что ни одно из его следствий не находится в противоречии с опытом. Первое начало термодинамики устанавливает соотношение между теплотой Q, работой А и изменением внутренней энергии системы ΔU.
Эквивалентность теплоты и работы
Постоянное эквивалентное соотношение между теплотой и работой при их взаимных переходах установлено в классических опытах Джоуля. Типичный эксперимент Джоуля заключался в следующем: падающий с известной высоты груз вращает мешалку, погружённую в воду, находящуюся в калориметре (груз, мешалка и калориметр с водой составляет термодинамическую систему); при этом совершается работа силы тяжести А = mgh. Вращение лопастей мешалки в воде вызывает нагревание воды в калориметре; теплота, переданная воде, равна произведению теплоёмкости калориметра с водой на произошедшее изменение температуры: Q = cΔt. После того, как указанный процесс закончен, система должна быть приведена к исходному состоянию. Это можно сделать путём мысленного эксперимента. Груз поднимается на исходную высоту, при этом извне над системой совершается работа, которая увеличивает энергию системы. Кроме того, от калориметра при охлаждении его до исходной температуры отнимается (передаётся в окружающую среду) теплота. Эти операции возвращают систему к исходному состоянию: все измеримые свойства системы приобретают те же значения, которые они имели в исходном состоянии. Процесс, в течение которого система изменяла свои свойства и в конце которого вернулась к исходному состоянию, называется круговым (циклическим) процессом или просто циклом.
Единственным результатом описанного цикла является отнятие работы от среды, окружающей систему, и переход в эту среду теплоты, взятой у калориметра. Сравнение двух величин (работы и теплоты) показывает постоянное отношение между ними, не зависящее от величины груза, размеров калориметра и конкретных количеств теплоты и работы в разных опытах.
Теплоту и работу в циклическом процессе целесообразно записать как интегральную сумму бесконечно малых (элементарных) теплот δQ и бесконечно малых (элементарных) работ δА,
 (1)
(1)
Здесь J - коэффициент пропорциональности, называемый механическим эквивалентом теплоты; его можно принять равным единице, выразив теплоту и работу в одних и тех же единицах измерения. Уравнение (1) представляет собой закон сохранения энергии для частного случая превращения работы в теплоту.
Рассмотрим следующий цикл: система переходит из состояния I в состояние II по некоторому пути 1; при этом передается теплота Q1 и совершается работа А1. Затем система возвращается в исходное состояние, причем обратный переход может совершаться как по тому же пути, что и прямой, т.е. за счет передачи теплоты –Q1 и совершения работы –А1, так и любым другим путем – за счет передачи теплоты Q2 и совершения работы А2, передачи теплоты Q3 и совершения работы А3 и т.д.

Для любого пути мы можем записать:
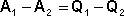 ,
,  , …
, … 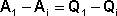 (2)
(2)
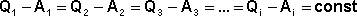 (3)
(3)
Величина "const" характеризует свойства системы; эта разность зависит только от начального и конечного состояния системы и не зависит от того, каким путём система переходит из начального состояния в конечное. Эту константу можно представить как изменение некоторой функции состояния (свойства системы, не зависящего от пути перехода системы из одного состояния в другое), называемой внутренней энергией системы U. Тогда
 (4)
(4)
 (5)
(5)
 (6)
(6)
Уравнения (4-5) являются математической записью 1-го начала термодинамики для конечного, уравнение (6) – для бесконечно малого изменения состояния системы. Теперь можно сформулировать первое начало термодинамики следующим образом:
Теплота, подведённая к системе, расходуется на совершение системой работы против внешних сил и на изменение внутренней энергии системы.
Изменение внутренней энергии системы равно количеству сообщенной системе теплоты минус количество работы, совершенной системой против внешних сил.
Уравнения (4-5) являются математической записью 1-го начала термодинамики. Выражение (4) можно переписать следующим образом:
 (7)
(7)
 (8)
(8)
В этом случае из уравнения (1) следует:
 (9)
(9)
Отсюда следует вывод, что в циклическом процессе внутренняя энергия системы не изменяется. Предположим, что данное условие не выполняется. Тогда, очевидно, циклический процесс можно провести таким образом, что после того, как система вернулась к исходному состоянию, внутренняя энергия системы не приняла начального значения, а увеличилась. В этом случае повторение круговых процессов вызвало бы накопление энергии в системе. Создалась бы возможность превращения этой энергии в работу и получения таким путём работы не за счет теплоты, а "из ничего", т.к. в круговом (циклическом) процессе работа и теплота эквивалентны друг другу, что показано прямыми опытами.
Исходя из вышеизложенного, можно сформулировать первое начало термодинамики также следующим образом:
Невозможно построить вечный двигатель 1-го рода, совершающий работу без затраты эквивалентного количества другого вида энергии
Полный запас внутренней энергии системы в результате циклического процесса возвращается к исходному значению, т. е. внутренняя энергия системы, находящейся в данном состоянии, имеет одно определённое значение и не зависит от того, каким изменениям система подвергалась перед тем, как прийти к данному состоянию. Иными словами, внутренняя энергия системы есть однозначная, непрерывная и конечная функция состояния системы.
Физически (в отличие от разобранного выше термодинамического понятия) под внутренней энергией понимается величина, которая характеризует общий запас энергии системы, включая энергию поступательного и вращательного движения молекул, энергию внутримолекулярного колебательного движения атомов и атомных групп, энергию вращения электронов в атомах, энергию, заключающуюся в ядрах атомов, и другие виды энергии, но без учёта кинетической и потенциальной энергии тела в целом. В настоящее время пока не имеется возможности определить абсолютную величину внутренней энергии какой-нибудь системы, т.к. неизвестным остаётся значение внутренней энергии при Т = 0 К.
Ещё одна формулировка 1-го начала термодинамики может быть получена из выражения (8) в применении к изолированным системам, в которых δQ = 0 и δА = 0:

отсюда 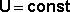 (10)
(10)
Внутренняя энергия изолированной системы постоянна
Эта формулировка 1-го закона термодинамики есть применённое к конкретным условиям и конечным системам количественное выражение общего закона сохранения энергии:
Энергия неуничтожаема и несотворяема; она может только переходить из одной формы в другую в эквивалентных соотношениях.
Рассмотрим приложение первого начала термодинамики для определения работы, совершаемой системой при различных термодинамических процессах (мы будем рассматривать простейший случай – работу обратимого равновесного расширения идеального газа).
Изохорный процесс (V = const; ΔV = 0).
Поскольку работа расширения равна произведению давления и изменения объема, для изохорного процесса получаем:
 (11)
(11)
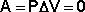 (12)
(12)
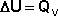 (13)
(13)
Изотермический процесс (Т = const).
Из уравнения состояния одного моля идеального газа получаем:
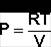 (14)
(14)
Отсюда:
 (15)
(15)
Проинтегрировав выражение (15) от V1 до V2, получим
 (16)
(16)
Изобарный процесс (Р = const).
При изобарном процессе работа газа против внешнего давления равна произведению давления газа на изменение объёма:
 (17)
(17)
Применим к выражению (17) уравнение состояния 1 моля идеального газа:
 ,
, 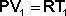 (18)
(18)
При подстановке этих значений в выражение (17) получим:
 (19)
(19)
Если в уравнении (19) принять разность температур равной 1 К, то А = R; следовательно, универсальная газовая постоянная R численно равна работе расширения, совершаемой 1 молем идеального газа при нагревании его на 1 К.
Адиабатический процесс (Q = 0).
При адиабатическом процессе работа расширения совершается за счёт уменьшения внутренней энергии газа:
 (20)
(20)
В случае, если теплоёмкость при постоянном давлении Cv не зависит от температуры (что справедливо для многих реальных газов), работа, произведённая газом при его адиабатическом расширении, прямо пропорциональна разности температур:
 (21)
(21)
Подставляя полученные выражения для работы различных процессов в уравнение (5), для тепловых эффектов этих процессов получим:
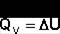 (22)
(22)
 (23)
(23)
 (24)
(24)
В уравнении (24) сгруппируем переменные с одинаковыми индексами. Получаем:
 (25)
(25)
Введем новую функцию состояния системы – энтальпию H, тождественно равную сумме внутренней энергии и произведения давления на объем:
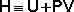
Тогда выражение (25) преобразуется к следующему виду:
 (26)
(26)
Т.о., тепловой эффект изобарного процесса равен изменению энтальпии системы.
Термохимия.
Термохи́мия — раздел химической термодинамики, в задачу которой входит определение и изучение тепловых эффектов реакций, а также установление их взваимосвязей с различными физико-химическими параметрами. Ещё одной из задач термохимии является измерение теплоёмкостей веществ и установление их теплот фазовых переходов.
Основным экспериментальным методом термохимии является калориметрия.
В термохимических уравнениях необходимо указывать агрегатные состояния веществ с помощью буквенных индек-сов, а тепловой эффект реакции (ΔН) записывать отдельно, через запятую. Например, термохимическое уравнение
аА(г) + bВ → cC + dD + 1531 кДж
показывает, что данная химическая реакция сопровождается выделением 1531кДж теплоты, если давление 101кПа, и относится к тому числу молей каждого из веществ, которое соответствует стехиометрическому коэффициенту в уравнении реакции.
Важнейшей величиной в термохимии является стандартная теплота образования (стандартная энтальпия образования). Стандартной теплотой (энтальпией) образования сложного вещества называется тепловой эффект (изменение стандартной энтальпии) реакции образования одного моля этого вещества из простых веществ в стандартном состоянии. Стандартная энтальпия образования простых веществ в этом случае принята равной нулю. В термохимии часто используют уравнения, в которых тепловой эффект относят к одному молю образовавшегося вещества, применяя в случае необходимости дробные коэффициенты.
Закон Гесса
В основе термохимических расчетов лежит закон Гесса.
Тепловой эффект (∆Н) химической реакции (при постоянных Р и Т) не зависит от пути ее протекания, а зависит от природы и физического состояния исходных веществ и продуктов реакции.
Следствия из закона Гесса:
Тепловые эффекты прямой и обратной реакций равны по величине и противоположны по знаку.
Тепловой эффект химической реакции (∆Н) равен разности между суммой энтальпий образования продуктов реакции и суммой энтальпий образования исходных веществ, взятых с учетом коэффициентов в уравнении реакции.
Закон Гесса может быть записан в виде следующего математического выражения:
. 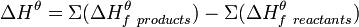
С помощью этого закона можно рассчитать энтальпии образования веществ, которые невозможно измерить.
Станда́ртные состоя́ния — в химической термодинамике условно принятые состояния индивидуальных веществ и компонентов растворов при оценке термодинамических величин.
Необходимость введения «стандартных состояний» связанa с тем, что термодинамические закономерности не описывают достаточно точно поведение реальных веществ, когда количественной характеристикой служит давление или концентрация. Стандартные состояния выбирают из соображений удобства расчётов, и они могут меняться при переходе от одной задачи к другой.
В стандартных состояниях значения термодинамических величин называют «стандартными» и обозначают нулем в верхнем индексе, например: G0, H0, μ0 — это соответственно стандартные энергия Гиббса, энтальпия, химический потенциал вещества. Вместо давления в термодинамических уравнениях для идеальных газов и растворов используют фугитивность, а вместо концентрации — активность.
Стандартные состояния ИЮПАК
Комиссия по термодинамике международного союза теоретической и прикладной химии (ИЮПАК) определила, что стандартное состояние – это состояние системы, условно выбранное в качестве стандарта для сравнения. Комиссия предложила следующие стандартные состояния веществ:
Для газовой фазы – это (предполагаемое) состояние химически чистого вещества в газовой фазе под стандартным давлением 100 кПа (до 1982 года – 1 стандартная атмосфера, 101 325 Па, 760 мм ртутного столба), подразумевая наличие свойств идеального газа.
Для беспримесной фазы, смеси или растворителя в жидком или твёрдом агрегатном состоянии – это состояние химически чистого вещества в жидкой или твёрдой фазе под стандартным давлением.
Для раствора – это (предполагаемое) состояние растворённого вещества со стандартной молярностью 1 моль/кг, под стандартным давлением или стандартной концентрации, исходя из условий, что раствор неограниченно разбавлен.
Для химически чистого вещества – это вещество в чётко определённом агрегатном состоянии под чётко определённым, но произвольным, стандартным давлением.
В определение стандартного состояния ИЮПАК не входит стандартная температура, хотя часто говорят о стандартной температуре, которая равна 25°С (298,15 К).
Уравнение Кирхгофа - соотношение, устанавливающее зависимость теплового эффекта химической реакции от температуры. Позволяет определять тепловой эффект реакции при любой температуре по стандартным энтальпиям (теплотам) образования, приводимым в термодинамических справочниках. Предложено Г. Р. Кирхгофом в 1858.
 = Cv,2 — Cv,1
= Cv,2 — Cv,1