ЕГЭ. Профильный уровень. Задание 18
Свойства функций в задачах с параметрами
Часть 1
Дихтярь М.Б.
Область определения функции: D (f)
Определение. Областью определения функции  называется множество всех действительных значений независимой переменной х, для каждого из которых функция принимает действительные значения.
называется множество всех действительных значений независимой переменной х, для каждого из которых функция принимает действительные значения.
функция 
| Область определения | |
| 1 /u | 
| |
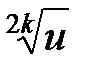
| 
| |

|  , v , v 
| |
| arcsinu | 
| |
| arccos u | 
| |
| arctg u | 
| |
| arcctg u | 
|
таблица 1.
1. Найдите все значения параметра а, при которых область определения функции  (1)не содержит двузначных натуральных чисел.
(1)не содержит двузначных натуральных чисел.
Решение. Очевидно, 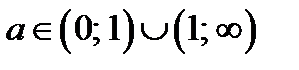 ,
,  .
.
1. Область определения функции, если 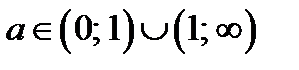 ,
,  найдём из неравенства
найдём из неравенства

Итак, область определения функции (1) состоит из всех х и а, удовлетворяющих неравенству
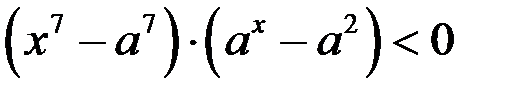 , где
, где 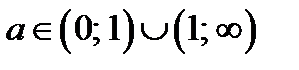 ,
,  (2).
(2).
2. Найдём множество решений неравенства (2) и определим, какие
значения параметра а удовлетворяютусловию задачи.
Замечание.
Если на множестве Х функции  и
и  одновременно возрастают или убывают, то
одновременно возрастают или убывают, то  .
.
Если на множестве Х одна из функций  или
или  возрастает, а другая убывает, то
возрастает, а другая убывает, то  .
.
1) Пусть  . Так как функция
. Так как функция  если
если  , убывает, а функция
, убывает, а функция  возрастает, то
возрастает, то

Так как неравенство  квадратное, коэффициент при
квадратное, коэффициент при 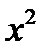 положительный и
положительный и  , и так как
, и так как  , то множеством решений этого неравенства является множество
, то множеством решений этого неравенства является множество 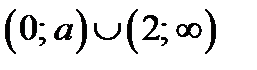 , где
, где  . Это множество содержит двузначные натуральные числа.
. Это множество содержит двузначные натуральные числа.
2) Пусть  Так как функции
Так как функции  ,
,  если
если  , возрастают, то
, возрастают, то 
Рассмотрим неравенство
 , где
, где  ,
,  (3)
(3)
а) Пусть  . Множеством решений неравенства (3) является интервал
. Множеством решений неравенства (3) является интервал  где
где  , который ни при каких значениях
, который ни при каких значениях  не содержит двузначные натуральных чисел.
не содержит двузначные натуральных чисел.
б) Пусть  . Тогда неравенство (3) принимает вид
. Тогда неравенство (3) принимает вид  , так как последнее неравенство не имеет решений, то
, так как последнее неравенство не имеет решений, то  удовлетворяет условию задачи.
удовлетворяет условию задачи.
в) Пусть  . Множеством решений неравенства (3) является интервал
. Множеством решений неравенства (3) является интервал  где
где  . Интервал
. Интервал  где
где  , не содержит двузначные натуральных чисел только, если
, не содержит двузначные натуральных чисел только, если 
Ответ.  .
.
Использование области определения функции для решения уравнений, неравенств, систем уравнений
Определение. Областью допустимых значений (ОДЗ) уравнения
(неравенства, системы уравнений, системы неравенств) называется множество таких значений переменной, для которой определена каждая функция, входящая в уравнение (неравенство, систему уравнений, систему неравенств).
2. Решите уравнение  .
.
Решение. ОДЗ уравнения (1) задаётся системой неравенств
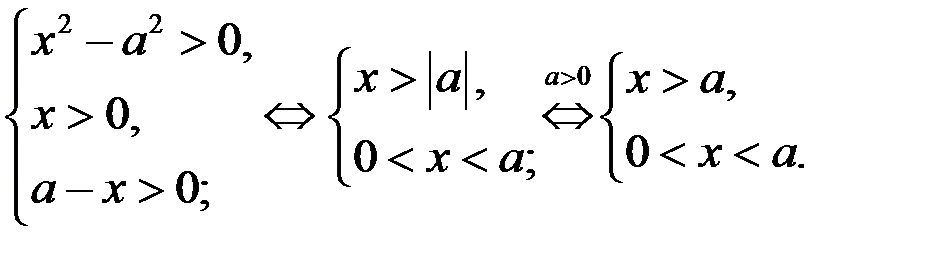
(Отметим: из неравенства 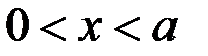 следует, что
следует, что  )
)
Так как последняя система не имеет решений, то ОДЗ уравнения пустое множество, а тогда уравнение (1) не имеет решений.
Ответ. Решений нет.
3. Решите уравнение 2  .
.
Решение. 1. Область определения функции  задаётся системой неравенств
задаётся системой неравенств

Так как в область определения функции  входят только
входят только  то корнями уравнения (1) могут быть только
то корнями уравнения (1) могут быть только 
2. Рассмотрим исходное уравнение при 
1) Пусть  Тогда уравнение (1) принимает вид
Тогда уравнение (1) принимает вид


Итак, если  , то корнем уравнения (1) является
, то корнем уравнения (1) является  .
.
2) Пусть  Тогда уравнение (1) принимает вид
Тогда уравнение (1) принимает вид


Итак, если 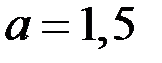 , то корнем уравнения (1) является
, то корнем уравнения (1) является 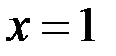 .
.
Ответ.  если
если  ;
;  если
если  ;
;
не имеет решений, если  .
.
4. Решите уравнение 
Решение. Отметим: функция  определена, если
определена, если  .
.
Замечание. 
ОДЗ уравнения (1) задаётся системой неравенств:

Из неравенства  следует, что
следует, что 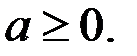 Тогда последняя система равносильна двойному неравенству
Тогда последняя система равносильна двойному неравенству  где
где  .
.
Итак, ОДЗ уравнения (1) состоит из  , где
, где  .
.
Так как  то из замечания следует, что уравнение (1) равносильно системе
то из замечания следует, что уравнение (1) равносильно системе

Итак, корнем уравнения является  где
где  .
.
Ответ.  если
если  ; нет корней, если
; нет корней, если 
5. Решите неравенство 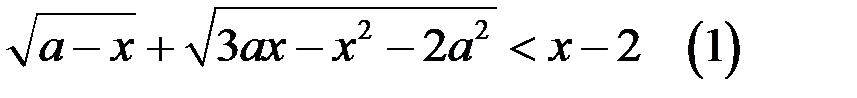 .
.
Решение. 1. ОДЗ неравенства (1) задаётся системой неравенств

Рассмотрим систему (2) при различных значениях параметра а.
1) Если  , то система (2) принимает вид
, то система (2) принимает вид 
Итак, если  то в ОДЗ неравенства (1) входит только
то в ОДЗ неравенства (1) входит только 
2) Если  то
то  . Тогда система (2) принимает вид
. Тогда система (2) принимает вид

Итак, если  то в ОДЗ неравенства (1) входит только
то в ОДЗ неравенства (1) входит только 
3) Если  то
то 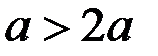 . Тогда система (2) принимает вид
. Тогда система (2) принимает вид

Итак, если  то ОДЗ неравенства (1) состоит из
то ОДЗ неравенства (1) состоит из 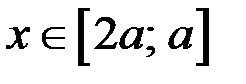 .
.
2. Рассмотрим неравенство (1) при различных значениях параметра а.
1) Если  и
и  то неравенство (1) не имеет решений, так как оно принимает вид
то неравенство (1) не имеет решений, так как оно принимает вид 
2) Если  и
и  то неравенство (1) принимает вид
то неравенство (1) принимает вид 
Итак,  является решением неравенства (1), если
является решением неравенства (1), если 
3) Если  , где
, где  то неравенство (1) не имеет решений, так как
то неравенство (1) не имеет решений, так как  , а
, а  (так как
(так как  , где
, где  ).
).
Ответ.  если
если  ; нет решений, если
; нет решений, если 
6. Решите систему уравнений
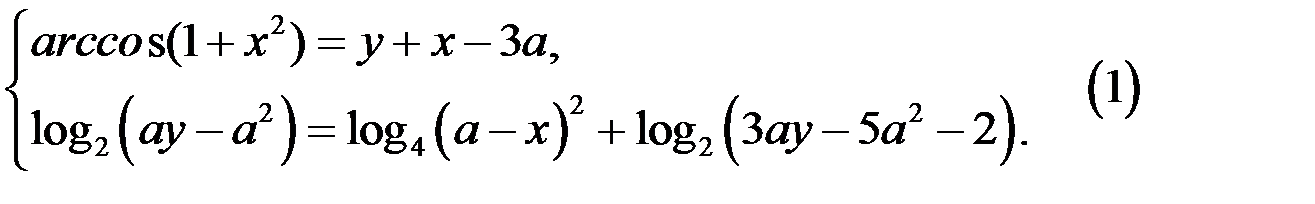
Решение. 1. Рассмотрим первое уравнение системы (1).
Область определения функции  задаётся двойным неравенством
задаётся двойным неравенством 
Так как область определения функции  содержит только
содержит только  то решением первого уравнения системы (1), а значит и системы (1), может быть только
то решением первого уравнения системы (1), а значит и системы (1), может быть только 
Отметим: 
Если  , то первое уравнение системы (1) принимает вид
, то первое уравнение системы (1) принимает вид

Итак,  ,
, 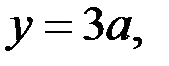 где
где  удовлетворяют первому уравнению системы (1).
удовлетворяют первому уравнению системы (1).
2. Второму уравнению системы (1) удовлетворяют  ,
,  , если
, если



Итак, если  , то
, то  ,
,  удовлетворяют и первому, и второму уравнениям системы (1). Это означает, что решением системы (1) является пара
удовлетворяют и первому, и второму уравнениям системы (1). Это означает, что решением системы (1) является пара 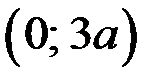 , если
, если  .
.
Ответ. 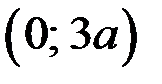 , если
, если  ; нет решений, если
; нет решений, если  .
.
Область значений функции  :
: 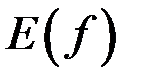
Определение. Множество всех значений функции  , если аргумент х принимает каждое значение из области определения функции, называется областью значений (множеством значений) функции
, если аргумент х принимает каждое значение из области определения функции, называется областью значений (множеством значений) функции 
Функция

| Область определения 
| Область значений 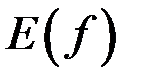
| |
| arcsin х | 
| 
| |
| arccos х | 
| 
| |
| arctg х | 
| 
| |
| arcctg х | 
| 
| |
 где где 
| 
| 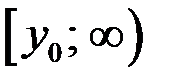
| |
 где где 
| 
| 
| |

| 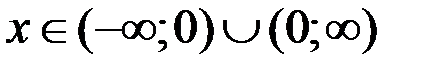
| 
| |
| 8. | 
| 
| 
|
таблица 2.
7. Решите уравнение  .
.
Решение. 1. Пусть 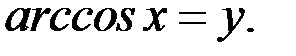 Так как областью значений функции
Так как областью значений функции  является отрезок
является отрезок  , то
, то 
Имеем 

Итак, решениями уравнения (1) являются
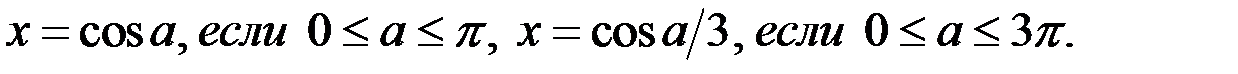
2. Определим, при каких значениях параметра а совпадают  Имеем
Имеем

Итак, если  , то
, то  Легко проверить, что при
Легко проверить, что при  решением уравнения (1) является
решением уравнения (1) является 
Ответ. Решений нет, если 
 если
если 


8. Решите уравнение 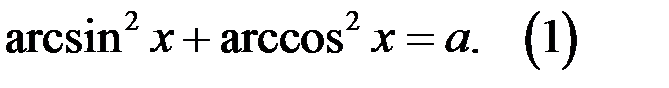 .
.
Решение. Имеем

1.Пусть  где
где  Тогда имеем
Тогда имеем


2. Рассмотрим уравнение
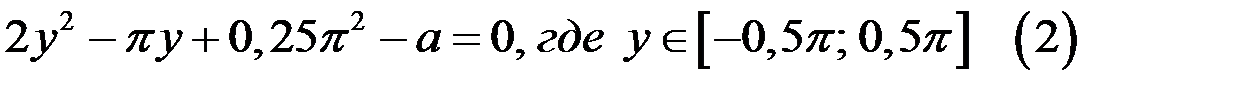
Дискриминант квадратного уравнения  равен
равен 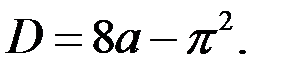
1) Пусть  Уравнение (3) имеет корень двойной кратности, равный
Уравнение (3) имеет корень двойной кратности, равный  если
если  . Так как
. Так как  то
то  является и корнем уравнение (2).
является и корнем уравнение (2).
Найдём корень уравнение (1) при  , если
, если  Имеем
Имеем
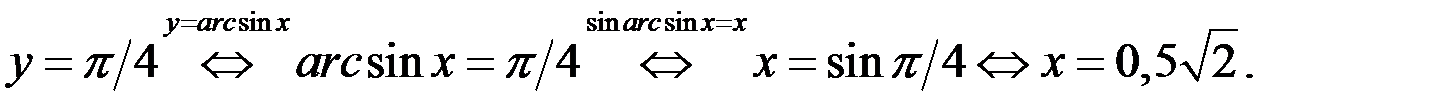
Итак, если  , то
, то  является корнем уравнения (1).
является корнем уравнения (1).
2) Пусть  Уравнение (3), если
Уравнение (3), если 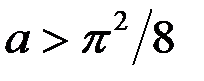 , имеет два разных корня:
, имеет два разных корня:  .
.
Определим, при каких значениях параметра а числа  принадлежат отрезку
принадлежат отрезку  т.е. являются корнями уравнения (2).
т.е. являются корнями уравнения (2).
а) Если  то
то



Итак, если 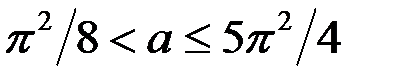 , то
, то  является корнем уравнения (3).
является корнем уравнения (3).
Найдём корень уравнение (1), если 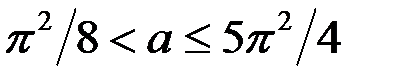 . Имеем
. Имеем

Итак, если 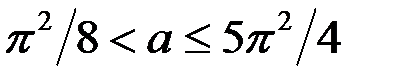 , то
, то  является корнем уравнения (1).
является корнем уравнения (1).
б) Если  то
то
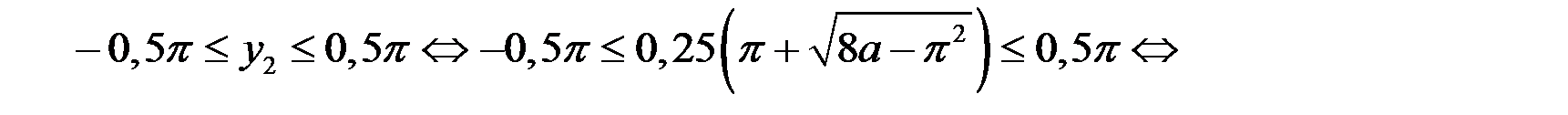

Итак, если 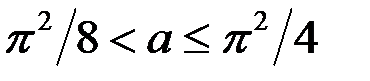 , то
, то  является корнем уравнения (3).
является корнем уравнения (3).
Найдём корень уравнение (1), если 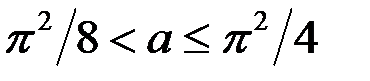 . Имеем
. Имеем
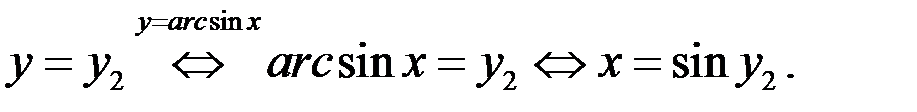
Итак, если  , то
, то  является корнем уравнения (1).
является корнем уравнения (1).
Если 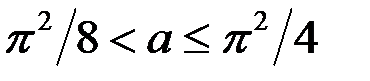 , то корни
, то корни  уравнения (1) не совпадают, так как функция
уравнения (1) не совпадают, так как функция  на отрезке
на отрезке  возрастает и
возрастает и  .
.
3) Пусть  Уравнение (3), если
Уравнение (3), если  а значит и исходное уравнение, не имеет корней.
а значит и исходное уравнение, не имеет корней.
Из 1) – 3) следует ответ.
Ответ. Корней нет, если 
 , если
, если 

 если
если 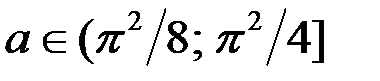 ;
;
 , если
, если  .
.
9. Решите уравнение 
Решение. Пусть  .
.
Итак, получили, что  .
.
Имеем


Последняя система не имеет решений, так как  и
и  не удовлетворяют неравенству
не удовлетворяют неравенству  .
.
Ответ. Решений нет, если 
Нахождение множества значений функции: 
Метод оценки
10. Найдите при различных значениях параметра а множество значений функции  .
.
Решение. Область определения функции – интервал 
Имеем

Оценим 
Очевидно, 
Рассмотрим функцию  при различных значениях параметра а.
при различных значениях параметра а.
а) Пусть  Тогда
Тогда 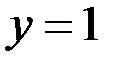 для любого
для любого 
Итак, если  то
то 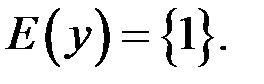
б) Пусть  Тогда
Тогда

Итак, если 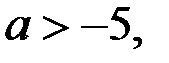 то
то 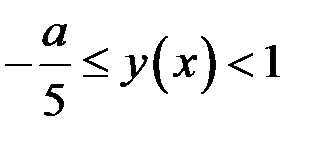 для любого
для любого  Это означает, что
Это означает, что 
в) Пусть  Тогда
Тогда
 Итак, если
Итак, если  то
то  для любого
для любого  Это означает, что
Это означает, что 
Ответ. Если  то
то 
если  то
то  если
если 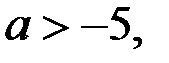 то
то 
Графический метод
11. Найдите при различных значениях параметра а множество значений функции  .
.
Решение. Построим график функции  при различных значениях параметра а.
при различных значениях параметра а.
Областью определения функции является интервал 
Так как функция 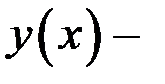 чётная, то множество значений функции на интервале
чётная, то множество значений функции на интервале  совпадает с множество значений этой функции на промежутке
совпадает с множество значений этой функции на промежутке 
Исследуем функцию  если
если 
Имеем 
Найдём производную функции  . Имеем
. Имеем

Итак, 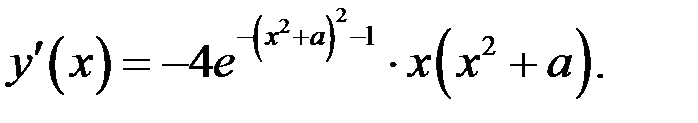
Из уравнения  найдём критические точки при различных значениях параметра а, если
найдём критические точки при различных значениях параметра а, если 
а) Пусть  Тогда
Тогда
 Так как
Так как  и
и  то уравнение
то уравнение  имеет два корня:
имеет два корня:  Очевидно,
Очевидно, 

 Критическая точка
Критическая точка  разбивают промежуток
разбивают промежуток  на промежутки
на промежутки 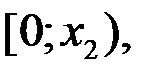
 . На рисунке 1 указаны знаки функции
. На рисунке 1 указаны знаки функции  на каждом промежутке. Из рисунка 1 делаем вывод: функция
на каждом промежутке. Из рисунка 1 делаем вывод: функция 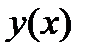 возрастает на отрезке
возрастает на отрезке  и убывает на промежутке
и убывает на промежутке 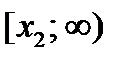 .
.
Найдём значение функции  в точках
в точках 
 .
.
Строим график функции  , если
, если 
Из рисунка 2 делаем вывод: если  то
то  .
.
б) Пусть 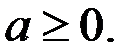
Так как  и
и  то уравнение
то уравнение  имеет единственный корень
имеет единственный корень 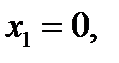 который не является критической точкой.
который не является критической точкой.
 На промежутке
На промежутке  производная
производная  отрицательная, поэтому на этом промежутке функция
отрицательная, поэтому на этом промежутке функция 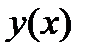 убывает.
убывает.
Строим график функции  , если
, если 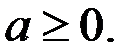
Из рисунка 3 делаем вывод: если  то
то 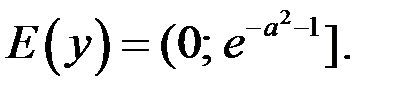 .
.
Ответ. Если  то
то 
если  то
то 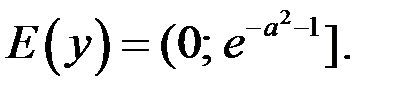
3. Рассматриваем функцию  как параметр
как параметр
Для того чтобы найти множество значений функции 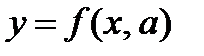 , надо определить при каких значениях у и а имеет решение уравнение
, надо определить при каких значениях у и а имеет решение уравнение  . Если для параметра
. Если для параметра  уравнение
уравнение  имеет решение при любом
имеет решение при любом  то
то  если
если 
12. Найдите при различных значениях параметра а множество значений функции  .
.
Решение. 1. Имеем

Если уравнения  и
и  (3) не имеют общих корней, то система (1) и уравнение (2) равносильны.
(3) не имеют общих корней, то система (1) и уравнение (2) равносильны.
Уравнения (2) и (3) имеют общие корни при тех значениях параметра а, при которых имеет решения система двух уравнений с двумя неизвестными 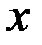 и а
и а

Итак, если  то уравнения (2) и (3) имеют общий корень. Это означает, что система (1) и уравнение (2) не равносильны, если
то уравнения (2) и (3) имеют общий корень. Это означает, что система (1) и уравнение (2) не равносильны, если  . Если
. Если  то система (1) и уравнение (2) равносильны.
то система (1) и уравнение (2) равносильны.
2. Найдём множество значений исходной функции при различных значениях параметра а.
Если 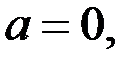 то исходная функция принимает вид
то исходная функция принимает вид 
Итак, если 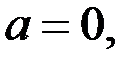 то
то 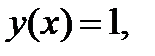 где
где  Тогда
Тогда 
Пусть 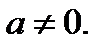
Множество значений исходной функции, при некотором значении параметра 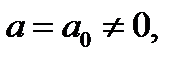 совпадает с множеством значений
совпадает с множеством значений  при которых уравнение
при которых уравнение  имеет решение, если
имеет решение, если 
1) Если  то уравнение (4) является линейным уравнением
то уравнение (4) является линейным уравнением 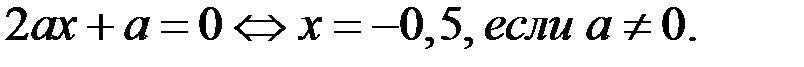
Итак, при любом  множеству значений исходной функции принадлежит
множеству значений исходной функции принадлежит  .
.
2) Если  то уравнение (4) является квадратным уравнением относительно х. Тогда уравнение (4) имеет решение, если дискриминант уравнения неотрицательный, то есть, если
то уравнение (4) является квадратным уравнением относительно х. Тогда уравнение (4) имеет решение, если дискриминант уравнения неотрицательный, то есть, если

3) Рассмотрим неравенство  , где
, где 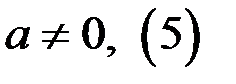 и уравнение (4) при различных значениях параметра
и уравнение (4) при различных значениях параметра 
а) Если  то неравенство (5) принимает вид
то неравенство (5) принимает вид 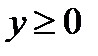 . Итак, если
. Итак, если  то
то  .Так как
.Так как  , то уравнение (4) имеет решения при любом
, то уравнение (4) имеет решения при любом 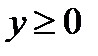 , если
, если  . Тогда
. Тогда  если
если 
Если 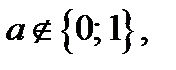 то
то
 .
.
б) Пусть 
Если  то
то

Если  то
то  . Тогда решением неравенства (6) являются
. Тогда решением неравенства (6) являются  где
где 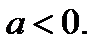 Так как
Так как  , то уравнение (4) имеет решение, при любом
, то уравнение (4) имеет решение, при любом  , если
, если  Тогда
Тогда  где
где 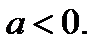
Если  .то
.то  . Тогда решением неравенства (6) являются
. Тогда решением неравенства (6) являются  где
где  Так как
Так как  , то уравнение (4) имеет решение при любом
, то уравнение (4) имеет решение при любом 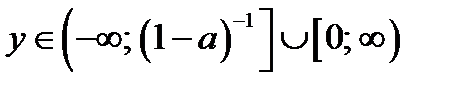 , если
, если  Тогда
Тогда  где
где 
в) Пусть  Тогда
Тогда 
Если  то
то

Тогда решениями неравенства (7) являются 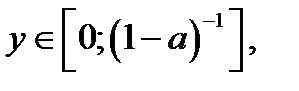 где
где  Так как
Так как  , то уравнение (4) имеет решение при любом
, то уравнение (4) имеет решение при любом  , если
, если  Тогда
Тогда  где
где 
Ответ.  если
если 
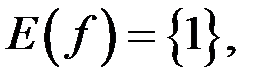 если
если 
 если
если 
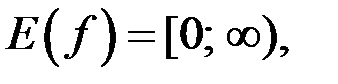 если
если 
 если
если 
Замена переменной.
Замечания. Для того чтобы найти множество значений функции 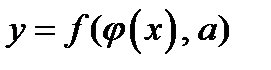 надо:
надо:
1) сделать замену переменной  ; 2) найти множество значений функции
; 2) найти множество значений функции  ; 3) найти множество значений функции
; 3) найти множество значений функции 
Множества значений функций 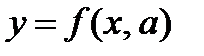 и
и  совпадают.
совпадают.
13. Найдите при различных значениях параметра а множество значений функции
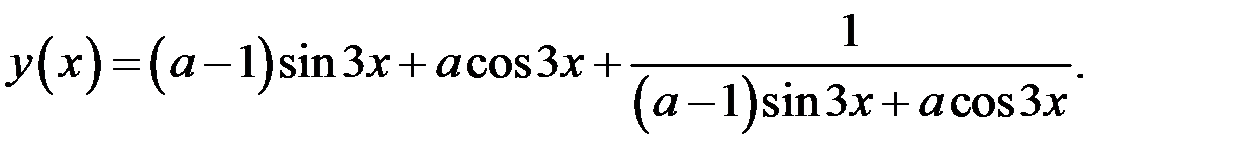
Решение. 1. Сделаем замену 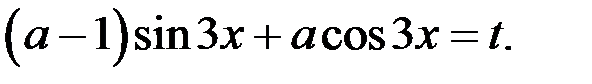 Тогда
Тогда  где
где  (следует из таблицы 2 и из того, что
(следует из таблицы 2 и из того, что  ).
).
Обозначим  Тогда
Тогда 
 Так как функция
Так как функция 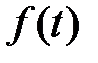 нечётная, то сначала найдём множество значений функции
нечётная, то сначала найдём множество значений функции 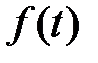 , если
, если  , а затем укажем множество значений функции
, а затем укажем множество значений функции 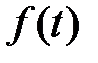 , если
, если 
На рисунке 4 изображён график функции  где
где 
Отметим: множеством значений функции  если
если  , является множество
, является множество  и
и 
2. Найдём множество значений функции  если
если 
1) Пусть 
Если  то
то  Из рисунка 5 следует: множеством значений функции
Из рисунка 5 следует: множеством значений функции 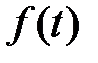 , где
, где  является множество
является множество  , если
, если  (рисунок 5 – эскиз графика функции
(рисунок 5 – эскиз графика функции