Если ОДЗ уравнения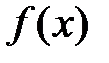 
есть множество X и для любого 
справедливы неравенства 
и 
, где A – некоторое число, то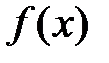 
24. Решите уравнение
.
Решение. Промежуток 
является ОДЗ уравнения.
Оценим левую часть уравнения (1).
Замечание. Если 
то 
равенство достигается, если 
Так как 
то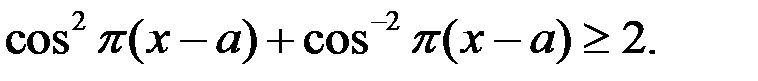 
Итак, левая часть уравнения (1) не меньше 2.
Оценим правую часть уравнения (1). Так как 
и 
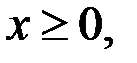то
Так как левая часть уравнения (1) не меньше 2, а правая часть уравнения (1) не больше 2, то уравнения (1) равносильно системе
Замечание: из равенства 
следует, что а является целым числом.
Ответ. 
, если а является целым числом;
а не является целым числом
25. Решите уравнение 
.
Решение. Оценим левую часть уравнения (1).
Из неравенства 
, имеем
.
Левая часть уравнения (1) не больше 2 и равна 2, если 
и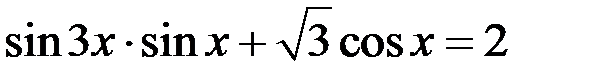 
. Так как 
то правая часть уравнения (1) не меньше 2 и равна 2, если 
Если 
то уравнение (1), равносильно системе
Отберём все значения x, входящие одновременно в обе серии решений. Найдём такие числа 
, что 
. Имеем
.
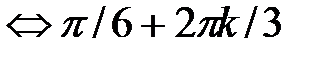
Таким образом, если то решениями системы (2), следовательно, и уравнения (1) являются 
.
Ответ. Если то 
;
если 
, то решений нет.
26. При каких значениях параметра а имеет единственное решение уравнение 
?
Решение. Очевидно, 
является решением уравнения (1) при любых значениях а.
Если 
то уравнение (1) принимает вид
Итак, если то уравнение (1) имеет бесконечное множество решений.
Пусть 
Перепишем уравнение (1) в виде 
. Так как
, то 
. Очевидно, 
.
Так как левая часть уравнения (2) не больше 3, а правая не меньше 3, то уравнение (2), а значит и исходное, равносильно системе
Отберём все значения x, входящие одновременно в обе серии решений. Найдём такие числа , что . Имеем
Равенство 
где 
рациональное число, выполняется в двух случаях.
1) Если 
рациональное число,то 
где 
и 
не равные нулю целые числа (в этом случае ). Тогда решениями исходного уравнения являются 
где не равное нулю целое число (уравнение имеет более одного решения).
2) Если а иррациональное число, то равенство 
выполняется только в случае, если 
и 
. Тогда исходное уравнение имеет единственное решение 
.
Ответ. а – любое иррациональное число.
27. Решите неравенство 
Решение. Неравенство (1) равносильно системе
Решением исходного неравенства может быть только 
если 
. Проверкой убеждаемся, что если , удовлетворяет исходному неравенству.
Ответ. Если 
то 
. если 
то решений нет.
28. Решите систему уравнений 
Решение. Имеем
Так как 
и 
то
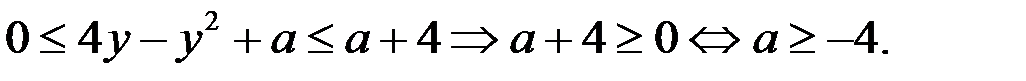
Итак, система (1) может иметь решение, если 
Так как 
если 
то из первого уравнения системы (1) следует, что 
где
Из второго уравнения системы (1) имеем
Система уравнений (1), если равносильна системе уравнений
Ответ. Если 
то 
.
если 
то система не имеет решений.
29. Решите систему уравнений
.
Решение. Рассмотрим второе уравнение системы (1).
Так как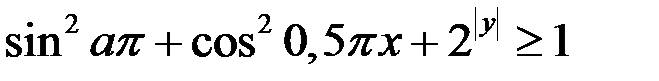 
и 
то уравнение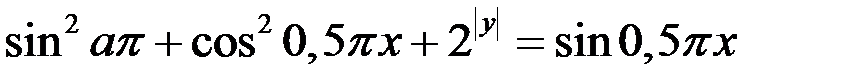 
равносильно системе
Итак, второе уравнение системы (1) имеет решение, если
Решением системы (1) может быть пара 
где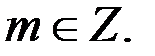 
Рассмотрим первое уравнение системы (1), если 
Отметим: х и а являются целыми числами.
Так как уравнение 
квадратное, то по теореме Виета
Так как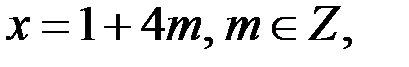 
то из равенства 
следуют следующие четыре случая.
1) 
Очевидно, 
и 
удовлетворяет условиям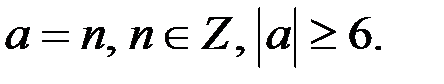 
Тогда, если 
то решениями системы (1) являются пары 
2) 
Не существуют целых чисел m таких, что 
Это означает, если 
, то система (1) не имеет решений.
3) 
Очевидно,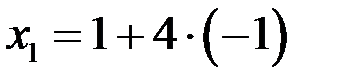 
и 
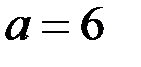удовлетворяет условиям 
Тогда, если 
то решением системы (1) является пара
4) 
Легко проверить, что не существует целого числа m такого, что 
Это означает, если 
то система (1) не имеет решений.
Ответ. Если то решения 
если то решение 
если 
, то система решений не имеет.
30. Решите систему неравенств 
Решение. Обозначим 
Тогда первое неравенство системы (1) принимает вид 
Из второго неравенства системы (1) имеем
Систему (1) перепишем в виде 
Замечание. Так как 
то 
(неравенство Коши).
Так как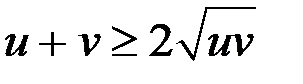 
, то из системы (2) следует
Система неравенств (1) равносильна системе уравнений
Ответ. Если 
то 