Диаграмма Карно выглядит как прямоугольная таблица с количеством клеток, зависящим от числа переменных булевой функции, для которой она строится.
Общее правило построения диаграмм Карно состоит в следующем. Число n переменных булевой функции делится на два. Если n - нечётное, то строкам диаграммы ставятся в соответствие наборы значений m = (n - 1)/2 первых булевых переменных, а столбцам – наборы значений оставшихся (n – m) булевых переменных. Если же n – чётное, то строкам и столбцам диаграммы соответствуют наборы m = n/2 переменных. Применяются также диаграммы, где число переменных по строкам и столбцам меняются местами, и диаграмма при нечетном числе n вытянута в длину.
При построении прямоугольной (или квадратной) таблицы с m строками и (n – m) столбцами, расположение наборов переменных булевой функции по строкам и столбцам должны удовлетворять следующему условию – соседние наборы должны отличаться не более чем в одной позиции (разряде). Например, для двух и трёх булевых переменных соответственно имеем:
00 01 11 10
000 001 011 010 110 111 101 100.
Таким образом, каждой клетке таблицы однозначно соответствует набор из n переменных булевой функции, первые m значений переменных набора соответствуют строке расположения клетки таблицы, последующие (n - m) - столбцу. Прямоугольная таблица заполняется значениями булевой функции по всем наборам.
Поскольку две соседние клетки отличаются значением только одной переменной (например,  и
и  ), то в случае расположения единиц в двух соседних клетках и минимизации в базисе ДНФ, мы склеиваем конституенты единицы по этой переменной (в нашем случае по x). В случае минимизации в базисе КНФ при расположении нулей в двух соседних клетках, склеиваем конституенты нуля по соответствующей переменной.
), то в случае расположения единиц в двух соседних клетках и минимизации в базисе ДНФ, мы склеиваем конституенты единицы по этой переменной (в нашем случае по x). В случае минимизации в базисе КНФ при расположении нулей в двух соседних клетках, склеиваем конституенты нуля по соответствующей переменной.
Будем минимизировать в базисе ДНФ.
В общем случае на диаграмме нужно выделить одну или группу размером  ,
,  рядом стоящих единиц, таким образом, чтобы перекрыть одним выделением как можно больше единиц. При этом необходимо учитывать, что верхние и нижние ряды клеток рассматриваются как соседние. Аналогично следует рассматривать как соседние, левые и правые столбцы клеток. Выделенные группы должны образовывать или одну клетку, или линию, или прямоугольник, или квадрат. Такими группами должны быть выделены все единицы на диаграмме.
рядом стоящих единиц, таким образом, чтобы перекрыть одним выделением как можно больше единиц. При этом необходимо учитывать, что верхние и нижние ряды клеток рассматриваются как соседние. Аналогично следует рассматривать как соседние, левые и правые столбцы клеток. Выделенные группы должны образовывать или одну клетку, или линию, или прямоугольник, или квадрат. Такими группами должны быть выделены все единицы на диаграмме.
По выделенным группам составляем конъюнкции. Переменные, которые изменяются в выделенной группе, в конъюнкцию не входят, мы склеиваем конъюнкции по этим переменным. Составляем конъюнкцию из переменных, значение которых не изменяется в выделенной группе наборов. Из полученных конъюнкций составляем дизъюнкцию и получаем ДНФ булевой функции.
Если выделенные группы содержат только максимально возможное количество единиц и количество групп минимально возможно, то полученная ДНФ – минимальная ДНФ, МДНФ.
Рассмотрим пример, проведем минимизацию функции, заданной СДНФ:
 .
.
Строим диаграмму Карно и записываем в клетки таблицы значения функции на всех наборах.
| x\yz | 00 | 01 | 11 | 10 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Первая группа, выделенная светло-серым цветом, состоит из четырех клеток, переменные x и z в этой группе меняют свои значения, поэтому записываем только значение переменной, которое не меняется в выделенной группе -  . Фактически, в этой группе мы склеиваем конституенты единицы, например, по строкам по переменной z. Затем полученные две импликанты склеиваем по x. В результате склеивания получим простую импликанту -
. Фактически, в этой группе мы склеиваем конституенты единицы, например, по строкам по переменной z. Затем полученные две импликанты склеиваем по x. В результате склеивания получим простую импликанту -  .
.
Во второй группе, состоящей из двух клеток, выделенных темно-серым цветом, не меняется значение переменной x, ее значение в обоих наборах -  и значение переменной z. Получаем конъюнкцию -
и значение переменной z. Получаем конъюнкцию -  . Получаем такую же МДНФ как и при минимизации методом Квайна:
. Получаем такую же МДНФ как и при минимизации методом Квайна:
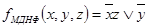 .
.
Минимизируем нашу функцию в базисе КНФ.
| x\yz | 00 | 01 | 11 | 10 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Поскольку это базис КНФ, то если переменная в наборе равна 0, мы берем ее без отрицания, если 1 – с отрицанием, между переменными составляем дизъюнкцию. В результате получим:
 .
.
Из МДНФ и МКНФ выбираем минимальную функцию с наименьшим рангом, в данном случае это МДНФ.
Рассмотрим еще пример.
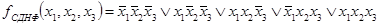 .
.
Можно выделить группы так
 \ \ 
| 00 | 01 | 11 | 10 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
В этом случае МДНФ имеет вид:
 .
.
Или так:
 \ \ 
| 00 | 01 | 11 | 10 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
 .
.
Рассмотрим минимизацию функции четырех переменных.
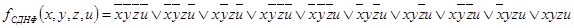
Составим диаграмму Карно и выделим группы.
| xy\zu | 00 | 01 | 11 | 10 |
| 00 | 1 | 1 | 1 | |
| 01 | 1 | 1 | ||
| 11 | 1 | 1 | ||
| 10 | 1 | 1 | 1 |
Рассмотрим группу фиолетового цвета, указанные ячейки образуют квадрат, если учитывать, что верхние и нижние ряды клеток рассматриваются как соседние и аналогично следует рассматривать соседними левые и правые столбцы клеток.
В квадрате не изменяется значение переменной y, соответственно получаем,-  и значение переменной u -
и значение переменной u -  . В результате получаем простую импликанту -
. В результате получаем простую импликанту -  . Квадрат, выделенный красным цветом, нам дает -
. Квадрат, выделенный красным цветом, нам дает -  . И, наконец, зеленый прямоугольник нам дает -
. И, наконец, зеленый прямоугольник нам дает - 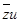 . В итоге имеем единственную МДНФ:
. В итоге имеем единственную МДНФ:
