ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ
Задача 1. Рассчитать напряжения в узлах электрической сети (рисунок 5), используя обобщенное уравнение состояния в матричной форме. Активными сопротивлениями элементов схемы замещения и потерями холостого хода трансформатора пренебречь.
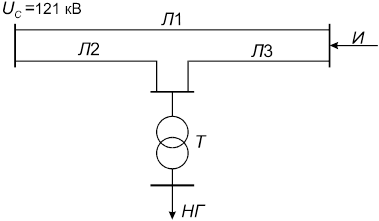
Рисунок 5 - Схема электрической сети
Исходные данные:
· линии электропередачи: Л1 - l = 30 км, 
= 0,42 Ом/км,
Л2 - l = 20 км, = 0,42 Ом/км,
Л3 -l = 15 км, = 0,42 Ом/км;
· силовой трансформатор Т - ТМН-6300/110: 
= 6,3 МВ·А,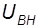 
= 115 кВ,
= 6,6 кВ, 
= 10,5 %;
· нагрузка НГ: 
= 6 МВ·А;
· источник И: 
= 16 МВ·А.
Решение:
1. Расчет схемы замещения. Схема замещения сети приведена на рисунке 6. По условиям задачи активными сопротивлениями и потерями холостого хода трансформатора в схеме замещения пренебрегаем.
Рисунок 6 - Схема замещения сети
Реактивные сопротивления элементов имеют следующие значения:
· для линий электропередачи:
хЛ = 
, (18)
где - погонное сопротивление, Ом/км,
- длина линии, км.
· для силового трансформатора:
(19)
где 
- напряжение короткого замыкания, %,
- номинальное напряжение обмотки высшего напряжения, кВ,
- номинальная мощность трансформатора, МВ·А.
При расчете нормального режима работы сети нагрузку и источник удобно представить источниками тока:
(20)
где 
- номинальное напряжение источника или нагрузки, кВ;
- их номинальная мощность, кВ·А.
При этом ток источника примем со знаком "+", а ток нагрузки - со знаком "-".
аналогично для нагрузки:
Поскольку сеть выполнена на два напряжения, то для составления уравнений ее схема замещения должна быть приведена к одному напряжению (основной ступени). Примем за основную ступень напряжение 110 кВ. В этом случае, приводя ток нагрузки со стороны 6 кВ к стороне 110 кВ, используя коэффициент трансформации трансформатора 
, можно записать:
где принимается как отношение номинального напряжения трансформатора со стороны, обращенной к основной ступени, к номинальному напряжению трансформатора со стороны приводимой. Следовательно:
Схема замещения, приведенная к ступени напряжения 110 кВ, с указанием параметров ее элементов изображена на рисунке 7. На этой схеме за балансный и базисный узел принят узел присоединения сети к системе 
. Для удобства составления уравнений этому узлу присвоен последний номер (номера узлов обведены "квадратами", номера ветвей - кружками).
Рисунок 7 - Схема замещения
Расчет напряжений в узлах электрической сети
В соответствии с (14) обобщенное уравнение состояния в матричной форме имеет вид:
.
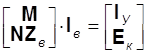Для составления матриц М и N представим граф сети в виде, показанном на рисунке 8.
Рисунок 8 - Граф сети
Матрица М строится следующим образом:
· число столбцов равняется числу ветвей;
· номер столбца соответствует номеру ветви;
· число строк равняется числу узлов за исключением базисного;
· номер строки соответствует номеру узла.
Матрица заполняется построчно. Для каждого из узлов рассматриваются все ветви графа, подходящие к этому узлу. Если ветвь соединена с узлом начальной вершиной, то в соответствующем столбце записывается число +1, если ветвь соединена с узлом конечной вершиной, то записывается -1, если у узла и ветви связи нет - 0.
Таким образом, для рассматриваемой задачи матрица М имеет вид:
С учетом приведенной нумерации ветви 1, 2, 3 графа сети (рисунок 8) составляют подграф-дерево, которому соответствует подматрица М a, ветвь 4 принята хордой, ей соответствует подматрица М b.
Матрица 
составляется следующим образом:
· число столбцов равно числу ветвей;
· номера столбцов соответствуют номерам ветвей;
· число строк соответствует числу независимых контуров (хорд);
· номера строк соответствуют номерам независимых контуров.
Если направление ветви совпадает с направлением обхода контура, то в соответствующем столбце записывается число +1; если противоположно, то число –1; если ветвь вообще не входит в путь обхода контура - число 0.
Для рассматриваемой задачи матрица будет иметь вид:
.
Далее получим
(Ом);
; так как 
.
Тогда обобщенное уравнение примет следующую форму:
(21)
Полученному матричному выражению можно поставить в соответствие систему уравнений состояния в традиционном виде. Для этого произведем формальное перемножение матриц, стоящих в левой части выражения (21). Получим:
(22)
Для решения уравнений воспользуемся методом Гаусса с обратным ходом [1]. Суть этого метода состоит в последовательном исключении неизвестных. В результате преобразований матрица коэффициентов при неизвестных превращается в верхнюю треугольную, т.е. все ее элементы ниже главной диагонали превращаются в нулевые. В этом случае последнее уравнение оказывается разрешенным относительно своего неизвестного, и после его определения путем обратного хода с помощью элементарных подстановок находятся все остальные неизвестные. Отметим, что применение алгоритма Гаусса предполагает, что все диагональные коэффициенты системы уравнений не равны 0. Чтобы удовлетворить этому условию, переставим в системе (22) второе и третье уравнения:
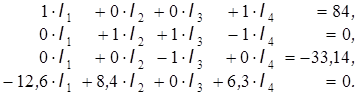
Найдем коэффициент 
:
,
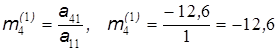где 
- коэффициенты уравнений.
Первое уравнение умножим на 
и вычтем его из четвертого:
Найдем коэффициент 
:
Умножим второе уравнение на 
и вычтем его из четвертого уравнения:
Найдем коэффициент 
:
Умножим третье уравнение на 
и вычтем его из четвертого уравнения:
Разделим последнее уравнение на 27,3:
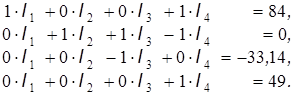
В матричной форме эта система будет иметь вид:
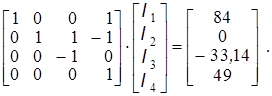
Далее последовательной подстановкой найдем неизвестные токи ветвей:
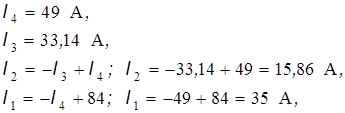
(А).
Найдем падения напряжения на ветвях 
:
(В).
(В).
Учитывая, что 
, найдем 
:
.
Для нахождения обратной матрицы 
воспользуемся методом Гаусса без обратного хода, алгоритм которого аналогичен алгоритму метода Гаусса с обратным ходом, но в этом случае обнуляются и элементы, находящиеся выше главной диагонали.
Поставим в соответствие исходной матрице 
справа единичную диагональную матрицу:
.
Будем выполнять операции по методу Гаусса одновременно с обеими матрицами. Как и в предыдущем случае, прежде чем воспользоваться алгоритмом Гаусса, переставим вторую и третью строки , чтобы исключить нулевой элемент из ее главной диагонали:
.
Далее по алгоритму Гаусса будем исключать элементы выше и ниже главной диагонали полученной матрицы. Разделим вторые строки обеих матриц на –1:
.
Найдем коэффициент 
:
Умножим третье уравнение на и вычтем его из второго:
.
Таким образом, = 
.
Тогда
= 
· 
= 
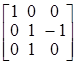(В).
Найдем напряжения узлов относительно "земли":
,
где Uб - напряжение базисного узла,
- единичная матрица.
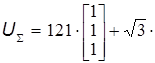
(кВ).
Найдем действительное значение напряжения узла 2. Поскольку напряжение узла 2, полученное в процессе расчета, соответствует основной ступени и должно быть приведено к ступени 6,6 кВ (т.е. в обратную сторону), то коэффициент трансформации 
будет равен:
,
тогда
(кВ).
Задача 2. Рассчитать напряжения в узлах электрической сети (рису-нок 9), используя обобщенное уравнение состояния для разомкнутой сети. Активными сопротивлениями элементов схемы замещения, потерями холостого хода трансформатора пренебречь. Расчет выполнить по полным значениям мощностей узлов нагрузок.
Рисунок 9 - Схема электрической сети
Исходные данные:
· линии электропередачи: Л1 -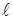 
= 20 км, 
= 0,42 Ом/км,
Л2 - 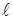= 5 км, = 0,47 Ом/км,
Л3 - 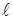= 10 км, = 0,45 Ом/км;
· силовые трансформаторы:
Т1 - 
= 1,6 МВ·А, 
= 35 кВ, 
= 11 кВ, 
= 6,5 %;
Т2 - = 0,4 МВ·А, = 10 кВ, = 0,4 кВ, = 4,5 %;
Т3 - = 0,63 МВ·А, = 10 кВ, = 0,4 кВ, 
= 5,5 %;
· нагрузки: НГ1 
= 0,3 МВ·А;
НГ2 
= 0,35 МВ·А;
НГ3 
= 0,5 МВ·А;
НГ4 
= 1,0 МВ·А.
Решение:
1. Расчет схемы замещения. Схема замещения сети приведена на рисунке 10.
По условиям задачи активными сопротивлениями схемы замещения и потерями холостого хода трансформаторов пренебрегаем.
Реактивные сопротивления элементов имеют следующие значения:
· для линий электропередачи в соответствии с (18):
Рисунок 10 - Схема замещения сети
· для силовых трансформаторов в соответствии с (19):
Для нагрузок в соответствии с (20) получим:
Следует отметить, что для источников (генератор, синхронный компенсатор, система) задающие токи будут иметь знак "+".
Перед составлением уравнений приведем параметры элементов схемы замещения к одному напряжению. С этой целью за основную ступень напряжения примем ступень 35 кВ. В этом случае реактивное сопротивление линий Л1 и нагрузки НГ4, работающих в сети напряжения 35 кВ, имеют истинные значения и не требуют пересчета. При расчете реактивного сопротивления трансформатора Т1 использовано напряжение 
= 35 кВ, поэтому сопротивление хТ1 также не требует пересчета.
При приведении реактивных сопротивлений линий Л2 и Л3, работающих в сети 10 кВ, а также трансформаторов Т2 и Т3, для расчета реактивных сопротивлений которых было использовано напряжение 10 кВ, может быть использовано следующее выражение:
где 
- коэффициент трансформации трансформатора Т1:
Тогда приведенные значения параметров схемы замещения будут равны:
Для тока нагрузки НГ1, включенной также в сети 10 кВ, получим:
.
Узлы нагрузки НГ2 и НГ3 включены в сети 0,4 кВ и отделены от основной ступени трансформаторами Т1 и Т2, Т3. Поэтому для них формула приведения тока будет содержать два коэффициента трансформации:
Тогда для токов нагрузок НГ2 и НГ3 будем иметь:
Схема замещения, приведенная к ступени напряжения 35 кВ, с указанием параметров ее элементов показана на рисунке 11.
Рисунок 11 - Схема замещения