Если функция f(x) удовлетворяет сформулированным условиям, то найдется такое δ, 0<δ≤min (c-a, b-c), что при любом выборе начального приближения на отрезке [c-δ,c+δ]Î[a, b]существует бесконечная итерационная последовательность, которая сходится к корню с.
В силу предположения о дифференцируемости функции f(x) и не равенстве нулю ее производной f `(x) уравнение эквивалентно на отрезке [a,b] уравнению
x=φ(x), где φ(x)= x – f(x)/f `(x),
Вычислим производную функцию φ(x)= x – f(x)/f `(x):
φ`(x)= 1 – [(f `(x))2- f(x) f ``(x)]/(f `(x))2 =- f(x) f ``(x)/ (f `(x))2
и оценим полученное выражение. Согласно неравенствам будем иметь
|φ`(x) |≤M | f(x)|/ m2.
Для дальнейшей оценки |φ`(x) | воспользуемся непрерывностью и равенством нулю функции f(x) в точке x=c:
lim f(x) = f(c) = 0.
Положим ε = m2/(2M), тогда для данного ε можно указать такое δ, 0<δ≤min (c-a, b-c), что для всех xÎ[c- δ, c+ δ] выполняется неравенство
| f(x) f(c)| = | f(x)| ≤ε=m2/(2M).
Выполняя преобразования, получим
|φ`(x) |≤(M / m2).(m2/2M) = ½.
Таким образом, функция φ(x) удовлетворяет на отрезке [c-δ,c+δ]Î[a, b] условию Липшица с постоянной α=1/2<1. Это означает, что уравнение можно решать методом итераций: при любом выборе нулевого приближения xo на отрезке [c-δ,c+δ] существует бесконечная последовательность {xn}, сходящаяся к коню x =c.
Итерационная последовательность для уравнения, сходимость которой мы только, что установили, является последовательностью метода касательных. Теорема доказана.
Требования близости нулевого приближения xo к искомому корню с является существенным для метода касательных. На рисунке нарисован график той же функции f(x), что и напредыдущим графике, однако xo выбрано дальше от корня с, чем в первом случае. В результате после первого же шага получается точка x1, которая не принадлежит исходному отрезку [a,b], и на этом процесс построения рекуррентной последовательности метода касательных обрывается.
Таким образом, до начала расчетов по данному методу для выбора нулевого приближения xo нужно знать область локализации искомого корня x=c. Если известен в общих чертах график функции f(x),, то ее легко определить по графику. В случае необходимости можно сделать несколько шагов по методу вилки. Затруднения связанные с предварительным исследованием уравнения, вполне окупаются высокой скоростью сходимости метода.
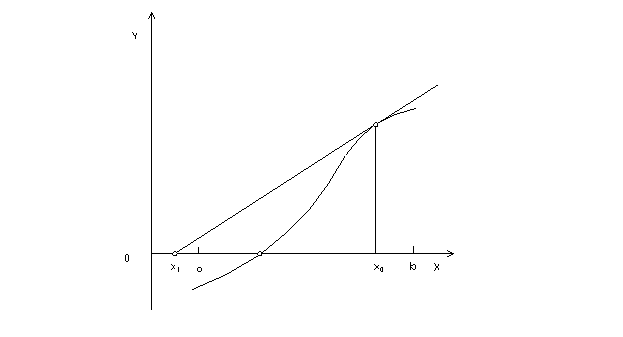
Рис.6. Случай, когда процесс построения последовательности {xn} обрывается из-за плохого выбора нулевого приближения
В качестве примера можно рассмотреть задачу извлечения квадратного корня из произвольного положительного числа a, a>0, который будем искать как решение уравнения
f(x) =x2 – a=0.
Рекуррентная формула метода Ньютона в данном случае принимает вид
xn=1 = xn – (xn2-a)/2xn.
Рассмотрим извлечение квадратного корня из числа 27. В качестве первого приближения примем 5.
| n | xn |
| 5,2000 | |
| 5,1961538461538500 | |
| 5,1961524227068300 | |
| 5,1961524227066300 |
Процесс сходимости весьма быстрый.
Рассмотрим пример по определению температуры воздуха внутри помещения (см. предыдущие разделы).
f(tв) =(tв + 20)50/2,5 – 1,5.600((82,5 - tв)/ 70)1,4 =0
f `(tв) = 20 tв – 1,4 . 1,5.600((82,5 -tв)/ 70)0,4(-1/70)= 20 + 18((82, 5-tв)/ 70)0, 4
Рекуррентная формула принимает вид
tв(n+ 1 ) = tв(n) –[(tв + 20)50/2,5 – 1,5.600((82,5 - tв)/ 70)1,4 ]/[ 20 +18((82,5 -tв)/ 70)0,4 ]
В качестве первого приближения примем среднее значение ранее определенного интервала [10, 25] – 17,5.
| n | xn |
| 17,5 | |
| 19,13591322 | |
| 19,1397908375762 | |
| 19,1397908595864 | |
| 19,1397908595864 |
Начиная с n=1 последовательность {xn} возрастает и приближается к коню x=c снизу. После третьего шага процесс «останавливается». Становится невозможным уловить разницу между xn=1 и xn, лежащей за пределами ошибки округления.
При оценки эффективности численных методов существенное значение имеют различные свойства:
1) универсальность;
2) простота организации вычислительного процесса и контроля за точностью;
3) скорость сходимости.
Выводы
1. Наиболее универсальным является метод вилки: он требует только непрерывности функции. Два других метода накладывают более сильные ограничения. В некоторых случаях это преимущество метода вилки может оказаться существенным.
2. С точки зрения организации вычислительного процесса все три метода очень просты. Однако и здесь метод вилки обладает определенным преимуществом. Вычисления можно начинать с любого отрезка [a, b], на концах которого непрерывная функция принимает значения разных знаков. Сходимость же метода итераций или касательных зависит от того, насколько удачно выбрано нулевое приближение.
3. Наибольшей скоростью сходимости обладает метод касательных. В случаях, когда подсчет значений функции сложен и требует больших затрат машинного времени, этот преимущество становится определяющим.