МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
дисциплины
"Прогнозирование и планирование деятельности предприятия"
Направление: 080100 "Экономика"
Специальность: 080102 «Мировая экономика»
Форма обучения: очная
Тула 2010
Методические указания составлены доцентом, к.э.н. Ветчинкиной Л.В. обсуждена на заседании кафедры "Мировая экономика"факультета экономики и права,
протокол № 9 от «30 » 09 2010 г.
Зав. кафедрой _______________________Белоцерковский В.И.
Методические указания пересмотрены и утверждены на заседании кафедры "Мировая экономика" факультета экономики и права,
протокол №_____ от «____»__________200__г.
Зав. кафедрой _______________________Белоцерковский В.И.
Тема 1: «Кластерный анализ»
Кластерный анализ позволяет из n объектов, характеризуемых k признаками, сформировать разбивку на однородные группы (кластеры). Однородность объектов определяется по расстоянию  (xi, xj), где xi = (xi1, …,x ik) и x j = (x j1,…, x jk) – векторы, составленные из значений k признаков i -го и j -го объектов соответственно.
(xi, xj), где xi = (xi1, …,x ik) и x j = (x j1,…, x jk) – векторы, составленные из значений k признаков i -го и j -го объектов соответственно.
Для объектов, характеризуемых числовыми признаками, расстояние определяется по следующей формуле:
 (хi, xj) =
(хi, xj) = 
Объекты считаются однородными, если  (xi, xj) <
(xi, xj) <  предельного.
предельного.
Графическое изображение объединения может быть получено с помощью дерева объединения кластеров – дендрограммы.
Пример
Пять производственных объектов характеризуются двумя признаками: объёмом продаж и среднегодовой стоимостью основных производственных фондов.
| Объект | |||||
| Объём продаж | |||||
| Среднегодовая стоимость основных производственных фондов |
Проведём классификацию этих объектов с помощью принципа «ближайшего соседа» Найдём расстояния между объектами по формуле  (хi, xj) =
(хi, xj) = 
Заполним таблицу.
| Объекты | |||||
| 2,24 | 5,10 | 12,65 | 11,18 | ||
| 3,61 | 11,18 | 9,49 | |||
| 7,62 | 6,08 | ||||
| 2,24 | |||||
Поясним как заполняется таблица.
На пересечении строки «i » и столбца «j » указано расстояние  (xi, xj) (результат округляем до двух цифр после запятой).
(xi, xj) (результат округляем до двух цифр после запятой).
Например, на пересечении строки «1» и столбца «3» указано расстояние
 (х
(х  , х
, х  ) =
) =  =5,10, а на пересечении строки «3» и столбца «5» указано расстояние
=5,10, а на пересечении строки «3» и столбца «5» указано расстояние  , x
, x  ) =
) =  6,08.
6,08.
Так как  (х
(х  , x
, x  ) = (x
) = (x  ,x
,x  ), то нижнюю часть таблицы можно не заполнять.
), то нижнюю часть таблицы можно не заполнять.
Применим «принцип «ближайшего соседа ». Находим в таблице наименьшее из расстояний (если таких несколько, то выберем любое из них). Это  2,24.
2,24.
Пусть  . Тогда мы можем объединить в одну группу объекты 4 и 5, то есть в объединённом столбце «4» и «5» будет наименьшее из соответствующих чисел столбцов «4» и «5» первоначальной таблицы расстояний. Аналогично поступаем и со строками «4» и «5». Получим новую таблицу.
. Тогда мы можем объединить в одну группу объекты 4 и 5, то есть в объединённом столбце «4» и «5» будет наименьшее из соответствующих чисел столбцов «4» и «5» первоначальной таблицы расстояний. Аналогично поступаем и со строками «4» и «5». Получим новую таблицу.
| Объекты | ||||
| 2,24 | 5,10 | 11,18 | ||
| 3,61 | 9,49 | |||
| 6,08 | ||||
| 4 и 5 |
Находим в полученной таблице наименьшее из расстояний (если таких несколько, то выбираем любое из них): 
 . Тогда мы можем объединить в одну группу объекты 1 и 2, то есть в объединённом столбце «1» и «2» предыдущей таблицы расстояний. Аналогично поступаем и со строками «1» и «2». Получим новую таблицу.
. Тогда мы можем объединить в одну группу объекты 1 и 2, то есть в объединённом столбце «1» и «2» предыдущей таблицы расстояний. Аналогично поступаем и со строками «1» и «2». Получим новую таблицу.
| Объекты | 1 и 2 | 4 и 5 | |
| 1 и 2 | 3,61 | 9,49 | |
| 6,08 | |||
| 4 и 5 |
Находим в полученной таблице наименьшее из расстояний (если таких несколько, то выбираем любое из них):  . Тогда мы можем объединить в одну группу объекты 1, 2,3, то есть в объединённом столбце «1»,2,3» будет наименьшее из соответствующих чисел столбцов «1 и 2» и «3» предыдущей таблицы расстояний. Аналогично поступаем и со строками «1 и 2» и «3». Получим новую таблицу.
. Тогда мы можем объединить в одну группу объекты 1, 2,3, то есть в объединённом столбце «1»,2,3» будет наименьшее из соответствующих чисел столбцов «1 и 2» и «3» предыдущей таблицы расстояний. Аналогично поступаем и со строками «1 и 2» и «3». Получим новую таблицу.
| Объекты | 1, 2, 3 | 4, 5 |
| 1, 2, 3 | 6,08 | |
| 4, 5 |
Мы получили два кластера: (1,2,3) и (4, 5).
На дендрограмме указаны порядок выбора элементов и соответствующие минимальные расстояния  .
.
Задача
Пять производственных объектов характеризуются двумя признаками: объёмом продаж и среднегодовой стоимостью основных производственных фондов.
| Объект | |||||
| Объём продаж | |||||
| Среднегодовая стоимость основных производственных фондов |
Провести классификацию этих объектов с помощью принципа «ближайшего соседа».
Замечание. Можно было проводить классификацию объектов с помощью принципа «дальнего соседа ».
Тема 2: «Дисперсионный анализ. Однофакторный анализ»
Дисперсионный анализ даёт общую схему проверки статистических гипотез, основанную на тщательном изучении различных источников вариации (изменчивости, неоднородности) в сложной ситуации. Он позволяет оценить влияние одного или нескольких факторов на результирующий признак.
На практике часто встречается ситуация, когда можно указать один фактор, влияющий на конечный результат, и этот фактор понимает конечное число значений. Такая ситуация может быть проанализирована при помощи однофакторного дисперсионного анализа.
Данные для однофакторного дисперсионного анализа – это k генеральных совокупностей. Однофакторный дисперсионный анализ сравнивает два источника вариации: между выборками (межгрупповая вариация) и внутри каждой выборки (внутригрупповая вариация). Каждая генеральная совокупность подчиняется нормальному распределению, причем все стандартные отклонения одинаковы.
Гипотеза H 0 утверждает, что все средние равны между собой. Альтернативная гипотеза Н 1 говорит о том, что не все средние равны между собой, (есть хотя бы две неравные средние).
Фактор А имеет k уровней. На каждом уровне проводится выборка объёмом n  2,…, k). Тогда общее число наблюдений равно n = n
2,…, k). Тогда общее число наблюдений равно n = n  .
.
Пусть x  - результаты j - й выборки. Отсюда S =
- результаты j - й выборки. Отсюда S = 
S 
 S
S 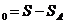
Статистика F=  . Доверительная вероятность
. Доверительная вероятность  ,
, 
По таблице F- распределения находим граничную точку F  Если F > F
Если F > F  то мы отклоняем гипотезу H
то мы отклоняем гипотезу H  на уровне значимости
на уровне значимости 
Пример
Предприятие решает вопрос о том, какую из трёх систем контроля качества выбрать. Все три системы были тестированы. Результаты тестов были отражены в таблице.
| Номер системы | Число выявленных бракованных изделий в партии продукции |
| 1, 2, 3, 0, 2, 1 | |
| 2, 3, 1, 0, 1 | |
| 2, 2, 3, 2 |
Проверим гипотезу об отсутствии влияния различий между системами на результаты тестирования систем. Доверительная вероятность равна 95%. Предполагается, что выбор- Ки получены из независимых нормальных генеральных совокупностей с одной и той же генеральной дисперсией.

H  различия между системами не влияют на результаты тестирования систем.
различия между системами не влияют на результаты тестирования систем.
H  различия между системами влияют на результаты тестирования систем.
различия между системами влияют на результаты тестирования систем.
 Заполним таблицу
Заполним таблицу
| Номер системы | Число изделий x 
| Сумма | n 
|
| 1, 2, 3, 0, 2, 1 | |||
| 2, 3, 1, 0, 1 | |||
| 2, 2, 3, 2 | |||
| Сумма | - |
Проверим, как заполняется таблица. Сумму элементов в каждой строке 2-го столбца пишем в соответствующей строке 3-го столбца, а число элементов в каждой строке 2-го столбца – в соответствующей строке 4-го столбца. В последней строке указана сумма чисел соответствующего столбца.
Тогда S = 
S 
S 
Статистика F = 
По таблице F -распределения находим горячую точку F 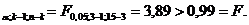
Мы принимаем гипотезу на уровне значимости 5%. Различия между системами контроля не влияют на результаты тестирования систем.
Задача
Предприятие решает вопрос о том, какую из трёх систем контроля качества выбирать. Все три системы были тестированы. Результаты тестов отражены в таблице.
| Номер системы | Число выявленных бракованных изделий в партии продукции |
| 2, 1, 0, 3, 3, 1 | |
| 3, 3, 2, 2, 1 | |
| 2, 2, 2, 3 |
Проверить гипотезу об отсутствии влияния различий между системами на результаты тестирования систем. Доверительная вероятность равна 99%. Предполагается, что выборки получены из независимых нормальных генеральных совокупностей с одной стороны и той же генеральной дисперсией.
Замечание. Excel позволяет провести однофакторный дисперсионный анализ. Воспользуемся надстройкой Пакет анализа.
Сервис  Анализ данных
Анализ данных  Однофакторный дисперсионный анализ
Однофакторный дисперсионный анализ  ОК. Откроется диалоговое окно, которое нужно заполнить. В графе Входной интервал указывается ссылка на ячейки, содержащие исходные данные. В графе Группирование нужно указать, как сгруппированы данные (по строкам, по столбцам). Если первые из ячеек содержат пояснительный текст, то рядом со словами Метки нужно поставить «галочку». Альфа (уровень значимости) по умолчанию предполагается равным 0,05. Если исследователя это не устраивает, то рядом со словами Альфа нужно указать требуемое значение. Также указываются параметры вывода (Входной интервал, Новый рабочий лист, Новая рабочая книга). ОК. Откроется итоговое окно.
ОК. Откроется диалоговое окно, которое нужно заполнить. В графе Входной интервал указывается ссылка на ячейки, содержащие исходные данные. В графе Группирование нужно указать, как сгруппированы данные (по строкам, по столбцам). Если первые из ячеек содержат пояснительный текст, то рядом со словами Метки нужно поставить «галочку». Альфа (уровень значимости) по умолчанию предполагается равным 0,05. Если исследователя это не устраивает, то рядом со словами Альфа нужно указать требуемое значение. Также указываются параметры вывода (Входной интервал, Новый рабочий лист, Новая рабочая книга). ОК. Откроется итоговое окно.
В первой таблице для каждой выборки будут указаны её объём (Счёт), сумма элементов (Сумма), выборочное среднее (Среднее) и выборочная дисперсия (Дисперсия). Вторая таблица имеет следующий вид. 

| Источник вариации | SS | d f | MS | F | p-значение | F крити -ческое |
| Между группами | S 
| k-1 | 
| 
| F 
| |
| Внутри групп | S 
| n-k | 
| |||
| Итого | S | n-1 |
Если P - значение меньше Альфа (то есть F > F критическое), то гипотеза H  отвергается.
отвергается.
Тема 3: «Двухфакторный дисперсионный анализ»
Рассмотрим влияние двух факторов А и В на конечный результат. Здесь дисперсионный анализ основывается на результатах эксперимента, проводимого на различных уровнях каждого из факторов.
Считаем, что взаимосвязь факторов отсутствует. Для простоты ограничимся случаем, когда для каждой пары уровней рассматриваемых факторов проводится по одному наблюдению (двухфакторный дисперсионный анализ без повторений).
Пусть n  - число уровней фактора А, n
- число уровней фактора А, n  число уровней фактора В. Тогда общее число наблюдений для всех возможных пар уровней факторов А и В равно n = n
число уровней фактора В. Тогда общее число наблюдений для всех возможных пар уровней факторов А и В равно n = n 
Гипотеза H  утверждает, что фактор А не влияет на конечный результат.
утверждает, что фактор А не влияет на конечный результат.
Гипотеза H  утверждает, что фактор В не влияет на конечный результат.
утверждает, что фактор В не влияет на конечный результат.
Пусть x  результат наблюдения при i-м уровне фактора А и j-м уровня фактора В. Введём следующие обозначения:
результат наблюдения при i-м уровне фактора А и j-м уровня фактора В. Введём следующие обозначения:


 =
= 


 ,
, 

S 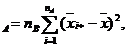 S
S 
S =  S
S 
Статистика F 
Статистика F 
Доверительная вероятность p,  По таблице F- распределения находим граничные точки F
По таблице F- распределения находим граничные точки F 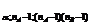 (для H
(для H  и F
и F  . (для H
. (для H 
Если F  > F
> F  то мы отклоняем гипотезу H
то мы отклоняем гипотезу H  на уровне значимости
на уровне значимости  .
.
Если F  > F
> F  то мы отклоняем гипотезу H
то мы отклоняем гипотезу H 
 на уровне значимости
на уровне значимости  .
.
Пример
Таблица содержит результаты наблюдений за влиянием факторов А и В на конечный результат
| Уровни фактора А | Уровни фактора В | |||
Оказывает ли влияние фактор А на конечный результат? Оказывает ли влияние фактор В на конечный результат? Доверительная вероятность равна 95%.
Заполним таблицу.
| Уровни фактора А | Уровни фактора В | Сумма | 
| |||
| 4,5 | ||||||
| Сумма | ||||||

| 4,33 |
Поясним, как заполняется таблица
В предпоследней строке указана сумма чисел соответствующего столба. В предпоследнем столбце указана сумма чисел соответствующей строки. Разделив эти суммы на число слагаемых и округлив результаты до двух цифр после запятой, мы получим последние строку и столбец.
Здесь число уровней фактора А равно n 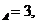 а число уровней фактора В равно n
а число уровней фактора В равно n 
 ×4) = 4,83.
×4) = 4,83.
S 
S 
S =  ×4×4,83
×4×4,83 
S 
H  : фактор А не влияет на конечный результат.
: фактор А не влияет на конечный результат.
H H  : фактор А влияет на конечный результат.
: фактор А влияет на конечный результат.
H  утверждает, что фактор В не влияет на конечный результат.
утверждает, что фактор В не влияет на конечный результат.
H 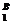 yутверждает, что фактор В влияет на конечный результат.
yутверждает, что фактор В влияет на конечный результат.
Доверительная вероятность p = 0,95  .
.
Статистика F 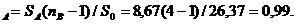
По таблице F - распределения находим граничную точку F  > F
> F  =0,99.
=0,99.
Мы принимаем гипотезу H  на уровне значимости 5%, то есть фактор А не влияет на конечный результат.
на уровне значимости 5%, то есть фактор А не влияет на конечный результат.
Статистика F 
По таблице F - распределения находим граничную точку
F  > F
> F 
Мы принимаем гипотезу H  на уровне значимости 5%, то есть фактор В не влияет на конечный результат.
на уровне значимости 5%, то есть фактор В не влияет на конечный результат.
Задача
Таблица содержит результаты наблюдений за влиянием факторов А и В на конечный результат.
| Уровни фактора А | Уровни фактора В | |||
Оказывает ли влияние фактор А на конечный результат? Оказывает ли влияние фактор В на конечный результат? Доверительная вероятность равна 99%.
Замечание. Excel позволяет провести двухфакторный дисперсионный анализ без повторений. Воспользуемся надстройкой Пакет анализа.
Сервис  Анализ данных
Анализ данных  Двухфакторный дисперсионный анализ без повторений
Двухфакторный дисперсионный анализ без повторений 
ОК. Откроется диалоговое окно, которое нужно заполнить. ОК. Откроется итоговое окно.
Если для соответствующего источника вариации (строки или столбцы) p -значение меньше Альфа (то есть F > F критическое), то соответствующая гипотеза Н  отвергается.
отвергается.
Excel позволяет также провести двухфакторный дисперсионный анализ с повторением. Сервис  Анализ данных
Анализ данных  Двухфакторный дисперсионный анализ с повторениями
Двухфакторный дисперсионный анализ с повторениями  ОК
ОК
Откроется диалоговое окно, которое нужно заполнить. В графе Число строк для выборки нужно указать число повторений. ОК. Откроется итоговое окно.
Тема 4: «Контролируемый прогноз»
Один из способов обеспечения точности прогнозов – использование трекинг-сигнала, который вычисляется по следующей формуле:
трекинг-сигнал = RSFE/MAD,
где RSFE =  итоговая сумма ошибок, MAD =
итоговая сумма ошибок, MAD =  - среднее абсолютное отклонение,
- среднее абсолютное отклонение,  - разность фактического и прогнозного значений в момент времени t, n – число наблюдений.
- разность фактического и прогнозного значений в момент времени t, n – число наблюдений.
При положительном (отрицательном) трекинг-сигнале фактические значения больше (меньше) прогнозных значений. У хорошего трекинг-сигнала итоговая сумма ошибок RSFE мала, то есть для него положительные ошибки приблизительно равны отрицательным ошибкам.
Вычисленные трекинг-сигналы следует сравнить с заранее определёнными верхней и нижней границами контроля. Если трекинг-сигнал выходит за границы контроля, то метод прогнозирования требует корректировки (например, изменения константы сглаживания в модели экспоненциального сглаживания).
Границы контроля выбирает сам исследователь. Обычно это или  4 (жесткий контроль), или
4 (жесткий контроль), или  8 (слабый контроль).
8 (слабый контроль).
Пример
Определим трекинг-сигналы по результатам первых шести кварталов, Границы контроля равны  4. Нужно ли менять константу сглаживания?
4. Нужно ли менять константу сглаживания?
Заполним таблицу.
| Квартал | A t | F t | et | RSFE | 
| Суммарная ошибка | MAD | Трекинг-сигнал |
| 3,8 | 2,2 | 3,2 | 2,2 | 3,2 | 1,6 | |||
| 5,6 | -1,6 | 1,6 | 1,6 | 4,8 | 1,6 | |||
| 4,3 | 0,7 | 2,3 | 0,7 | 5,5 | 1,38 | 1,67 | ||
| 4,9 | 5,1 | 7,4 | 5,1 | 10,6 | 2,12 | 3,49 | ||
| -1 | 6,4 | 11,6 | 1,93 | 3,32 |
Поясним, как заполняется таблица.
Значения первых трёх столбцов взяты из примера 106. 4-й столбец – это разность 2-го и 3-го столбцов. 6-й столбец – это абсолютные величины чисел 4-го столбца. Для получения чисел данной строки 5-го (7-го) столбца прибавляем к числу предыдущей строки 5-го (7-го) столбца число данной строки 4-го (6-го) столбца. Каждое число 7-го (5-го) столбца делим на соответствующее число 1-го (8-го) столбца, результат округляем до двух цифр после запятой и пишем в 8-м (9-м) столбце.
Так как все трекинг-сигналы (числа в последнем столбце) принадлежат интервалу (-4; 4), то константу сглаживания менять не нужно.
Задача
Определить трекинг-сигналы по результатам первых шести кварталов. Границы контроля равны  4. Нужно ли менять константу сглаживания?
4. Нужно ли менять константу сглаживания?
Тема 5: «Финансовое прогнозирование»
Целью финансового прогнозирования является определение ожидаемых финансовых результатов от деятельности компании в предстоящий период и потребности в финансировании. В литературе наряду с термином "финансовое прогнозирование" используется также термин "финансовое планирование".
Финансирование компании может осуществляться за счет как внутренних (прибыль, амортизация), так и внешних источников. Внутреннее финансирование производится в результате нормальной производственной деятельности компании, внешнее обусловлено капиталом, поступающим от инвесторов и банков.
При составлении финансового плана (прогноза) оцениваются результаты будущих коммерческих операций, приносящих доход, и связанные с ним расходы, что дает возможность заранее оценить потребность во внешнем финансировании.
Одним из методов планирования финансовых потребностей является метод процента от продаж, когда будущие расходы, активы и обязательства оцениваются на основе процента от предполагаемых продаж предстоящего периода. Получаемые таким образом данные используются для составления прогнозного балансового отчета. Превышение величины актива над пассивом (обязательствами и собственным капиталом) означает необходимость дополнительного внешнего финансирования
Пример
Составляется прогнозный балансовый отчет на следующий год при таких исходных данных:
продажи отчетного года - 20 млн. руб.;
ожидаемые продажи следующего года - 24 млн. руб.;
ожидаемая прибыльность продаж
следующего года - 5 %;
ожидаемый уровень дивиденда - 40 %
Результаты расчетов приведены в таблице в млн. рублей ("н/п" означает "не планируется"):
| Статьи баланса | Отчетный год | % от продаж | Планируемый год |
| Активы | |||
| Оборотные средства | 2,4 | ||
| Основные средства | 4,8 | ||
| Итого активов | 7,2 | ||
| Обязательства и собственный капитал | |||
| Краткосрочные обязательства | 2,4 | ||
| Долгосрочные обязательства | 2,5 | н/п | 2,5 |
| Итогообязательств | 4,5 | 4,9 | |
| Обыкновенные акции | 0,1 | н/п | 0,1 |
| Дополнительный капитал | 0,2 | н/п | 0,2 |
| Нераспределенная прибыль | 1,2 | 1,92 | |
| Итого собственный капитал | 1,5 | 2,22 | |
| Итого обязательства и собственный капитал | 6,0 | 7,12 |
Нераспределенная прибыль планируемого года определяется следующим образом: нераспределенная прибыль отчетного года + планируемая чистая прибыль - выплачиваемый дивиденд, что в результате дает 1,2 + 0.05 х 24 -0,4 х 0.05 х 24 = 1,92 млн. руб.
Поскольку прогнозный размер активов (7,2 млн. руб.) превышает прогнозный размер обязательств, потребуется внешнее финансирование в размере 7,2 - 7,12 = 0,08 млн. руб.
Метод процента от продаж является простым, но недостаточно точным, поскольку не учитывает возможного несовпадения будущих входящих и исходящих денежных потоков, что потребует дополнительного финансирования. Более точным будет метод составления сметы ожидаемых доходов и расходов (бюджета) компании.
Этапы подготовки бюджета включают:
прогноз продаж (план сбыта);
определение ожидаемого объема производства (производственный план);
расчет производственных затрат и эксплуатационных расходов;
определение движения денежных средств (кассовый план);
составление прогнозного бюджета.
План сбыта является основой и оказывает влияние на все части бюджета. При его составлении обычно рассматриваются ожидаемые поквартальные продажи в натуральном выражении, умножение которых на цены дает объем продаж в денежном выражении. Если планируется дебиторская задолженность, используется норматив поступления средств в квартале продаж (например, 70 %), в следующем квартале (например, 28%) и безнадежные к взысканию долги (в данном случае 2%).
На основе плана сбыта разрабатывается производственный план. При этом количество единиц, подлежащих изготовлению в данном квартале, определяется следующим образом: планируемые продажи + желаемый запас готовой продукции на конец квартала (например, 10 %) - запас готовой продукции на начало квартала.
Затем определяются прямые затраты на материалы для производимых изделий с учетом желаемых запасов на конец квартала (например, 10 %) и имеющихся запасов на начало квартала, после чего на основе цены единицы материалов определяется стоимость их закупок. Если расчеты за материалы предполагается проводить частично в данном, а частично в следующем квартале, составляется график ожидаемых денежных выплат.
Следующий этап - определение прямых затрат на оплату труда. Для их расчета ожидаемый объем производства за каждый квартал умножается на число часов работы, необходимых для производства одного изделия и на стоимость одного часа труда.
Далее составляется смета общезаводских накладных расходов, связанных с производством, таких, как заводская арендная плата, плата за энергоресурсы, амортизация и др. Эти расходы следует разделить на переменные и постоянные для последующего анализа точки безубыточности и операционного рычага (см. тему 3). Следует также учитывать, что амортизация не требует затрат денежных средств и должна вычитываться из сметы общезаводских накладных расходов при определении денежных выплат. Нормативом при таких расчетах является ставка переменных накладных расходов на один час прямых затрат труда.
Следующим шагом будет составление сметы торговых и административных расходов. Нормативом здесь являются переменные расходы на одно изделие, умножением которых на ожидаемый объем продаж в натуральном выражении получают общие переменные расходы.
Постоянные торговые и административные расходы могут включать ожидаемые расходы на рекламу, страховку, зарплату служащих, аренду, налоги и др.
Произведенные расчеты учитывают все источники доходов и расходов, связанные непосредственно с производством продукции и ее продажей. При этом, однако, не учитываются возможное несовпадение доходов и расходов в течение года, а также дополнительные расходы, например, на закупку оборудования, которое обычно осуществляется по отдельному плану, и на уплату налогов предыдущего года.
Для учета всех этих факторов необходимо составлять кассовый план, охватывающий обычно следующие основные разделы:
денежные поступления за каждый квартал, включающие кассовый остаток на его начало, денежные средства от покупателей продукции и прочие денежные поступления;
выплаты в каждом квартале, включающие все запланированные платежи;
излишек или дефицит денежных средств в каждом квартале, равный разнице между денежными поступлениями и денежными выплатами;
дополнительное финансирование в случае дефицита денежных средств (например, за счет краткосрочного банковского кредита), где будет отражаться получение кредитов и их погашение с процентами.
Кассовый остаток с учетом возможного дополнительного финансирования на конец рассматриваемого квартала будет кассовым остатком на начало следующего квартала.
Заключительный этап - составление прогнозного отчета о прибылях и убытках (доходах и расходах), который имеет вид:
Продажи
переменные производственные расходы
переменные торговые и административные расходы
Прибыль до вычета постоянных расходов
постоянные общезаводские накладные расходы
постоянные торговые и административные расходы
Прибыль до выплаты процентов и налогов
расходы на выплату процентов
Прибыль до налогообложения
налог на прибыль
Чистая прибыль
Контрольные вопросы
1. Для чего осуществляется финансовое прогнозирование?
2. Какие документы составляются при финансовом прогнозировании?
3. Какими методами осуществляют финансовое прогнозирование?
4. В чем сущность, преимущества и недостатки метода процента от продаж?
5. Какие выводы можно сделать на основе прогнозного балансового отчета?
6. Каковы этапы составления прогнозного отчета о доходах и расходах?
7. Для чего следует выделять ожидаемые переменные и постоянные расходы?
8. С какой целью составляется кассовый план?
9. Какие выводы можно сделать по прогнозному отчету о доходах и расходах?
Тема 6: «Прогнозирование рыночных тенденций»
Приложением к данной теме является алгоритмический модуль ФАЙЛ.xls (7Kb)
"Рынок" представляет собой крайне сложную кибернетическую модель с очень большим количеством внутренних и внешних факторов. Прогнозирование какого-либо фактора рыночной ситуации (например, объем продаж конкретной фирмы) невозможно только на основе тенденции самого фактора. Почему? Поведение отдельного рыночного фактора, позволю себе аналогию, подобно поведению бабочки в полете. Вспомните, как летит бабочка: ее полет выглядит с внешней стороны как "порхание" без определенной цели, хотя, очевидно, что она стремится к определенной цели - к цветку. Мы не обращаем внимания на внешние факторы, влияющие на бабочку: ветер, атмосферное давление, высота от земли, гравитация и т.п., и на внутренние: ее собственные силы, система ориентирования и т.п. Суть в том, что мы со стороны не можем предсказать, к какому цветку прилетит бабочку. Так же ведет себя и изучаемый отдельный рыночный показатель. Очевидно, что на объем продаж фирмы (как отдельный показатель) могут влиять продажи конкурентов, тенденции емкости сегмента, их объемы продажи, конъюнктура товаров-заменителей, сопутствующих товаров (услуг) и многие другие факторы. И такое влияние обусловливает поведение не только фактора объема продаж, но и любого внутрифирменного показателя. Тем не менее, такой прогноз необходим в рамках маркетинговых исследований. И поэтому давайте рассмотрим методику, которая, с одной стороны, не