Определение длин линий по картам имеет большое значение для многих отраслей науки и практики, использующих в своей работе данные о форме и протяженности географических объектов. Важно научиться измерять длины линий на географических картах мелких масштабов и обрабатывать полученные результаты, используя различные методы.
При определении длин извилистых линий возникают две задачи:
ü измерение извилистой линии по карте;
ü переход от результатов измерения к вычислению длины этой линии в натуре с учетом изменения масштаба длин, генерализации и других факторов.
При учете изменения масштаба длин в пределах карты необходимо установить средний масштаб для измеряемой линии и умножить на него результаты непосредственных измерений на карте.
Основным инструментом для определения длин линий является циркуль-измеритель. При использовании этого инструмента необходимо знать цену его раствора. Под ценой раствора циркуля-измерителя понимается число метров или километров, соответствующее этому раствору на данном участке карты с учетом ее частного масштаба и деформации бумаги.
Для определения цены раствора d следует измерить на карте линию, длина которой известна в натуре. В качестве такой линии обычно выбирается длина дуги меридиана или параллели.
Если выбрана длина дуги меридиана, то цена деления инструмента d рассчитывается из соотношения
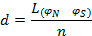
где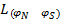 
– длина дуги меридиана в метрах или километрах между параллелями с широтами 
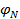и 
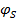; n – число отложений (делений) инструмента в измеренной дуге меридиана.
Значение 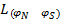может быть получено из выражения
,
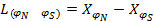где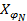 
и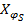 
– длины дуг меридиана от экватора до соответствующей параллели, выписываются из картографических таблиц или вычисляются по формуле
|
|
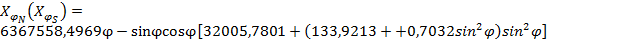
Если в качестве линии, длина которой в натуре известна, использована длина дуги параллели L, то d получим из соотношения
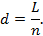
Здесь L – соответствующий элемент параллели между меридианами с разностью долгот Δλ на поверхности эллипсоида:
,
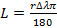где r – радиус параллели, выписывается из картографических таблиц или вычисляется по формуле
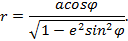
Тогда
,
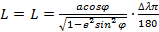где a = 6 378 245 м; е2 = 0,00669124 (элементы эллипсоида Красовского).
На картах крупных и средних масштабов отрезки прямых и ломаных линий измеряют с помощью циркуля-измерителя и поперечного масштаба. Труднее обстоит дело с измерением длин извилистых линий: рек, береговых линий и пр.
Для увеличения точности измерений рекомендуется применять циркули-измерители с малыми растворами: 1,0; 1,5; 2,0; 4,0 мм.
При использовании циркуля-измерителя его иглу устанавливают в начальную точку кривой и подсчитывают число отложений в пределах измеряемой линии. Во избежание просчетов число отложений измерителя подсчитывают при обводе кривой в прямом nпр и обратном nобр направлениях, затем определяют nср. Таким образом, длина линии
l = dn ср.
При определении длин извилистых линий с помощью циркулей-измерителей фактически измеряется не сама извилистая линия, а ломаная, получаемая при многократном отложении измерителем отрезков, равных размеру его раствора. Очевидно, что чем меньше раствор измерителя, тем больше длина ломаной линии будет приближаться к истинной длине измеряемой извилистой линии.
Большинство способов определения длин извилистых линий основано на измерении их поочередно двумя циркулями-измерителями с различными растворами (например, 1 и 4 мм) и вычислении по результатам этих измерений приведенных длин линий.
|
|
Метод Н.М. Волкова. Длина извилистой линии, измеряемой по карте данного масштаба, возрастает по мере уменьшения раствора циркуля. Если отложить на графике по оси абсцисс значения d, а по оси ординат соответствующие им значения l, то получим кривую, удовлетворяющую уравнению параболы. При уменьшении размера раствора, в пределе стремящегося к нулю, можно получить действительную, или приведенную, длину lпр линии с учетом всех ее извилин и изгибов.
Измерив одну и ту же линию дважды циркулем с растворами d1 и d2 (d 1< d2), получим два значения длины линии – l1 и l2 (l1 > l2):
; 
,
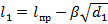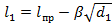где β – коэффициент, зависящий от извилистости линии,
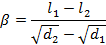
Окончательно приведeнная длина линии
.
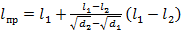Метод А.К. Маловичко. Для определения аналитической зависимо сти между длинами линий l1 и l2, полученными с использованием циркулей с растворами d1 и d2, и приведенной длиной lпр извилистой линии используются правильные геометрические линии. А.К. Маловичко для определения lпр предложил аппроксимировать извилистые линии окружностями. Тогда приведенная длина
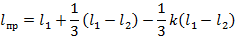
где k – поправочный коэффициент,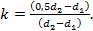 
Метод Ю.С. Фролова. Дальнейшие изыскания в области определе ния аналитических зависимостей между длинами, полученными из изме рений, и приведенными длинами для правильных геометрических линий привели к использованию для приведения линии, состоящей из сопряженных полуокружностей. В этом случае
|
|
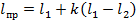
где l1=d1n1 l2=d2n2 (n1 и n2 – число отложений измерителя при определении l1 и l2);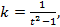 
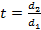
Любой метод определения длин извилистых линий предполагает выполнение соотношения между ценой делений растворов измерителей d1 < d2 и полученными длинами l1 > l2.