Комплексные числа как расширение понятия действительного числа
Известно, что в области действительных чисел некоторые квадратные уравнения имеют два корня, некоторые – один корень и некоторые – ни одного. Такое положение вещей издавна тревожило математиков, казалось неестественным, и не раз высказывалась идея о том, что, кроме действительных корней, такие уравнения имеют еще «мнимые», воображаемые корни. Например, итальянский математик Кардано в XVI веке писал (здесь мы приводим современные обозначения), что если предположить, что можно извлечь корень из отрицательного числа, то числа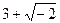 
и 
являются корнями квадратного уравнения 
(проверьте по теореме Виета).
Таким образом, Кардано ввел в рассмотрение «мнимые величины» - квадратные корни из отрицательных чисел. Правда, среди действительных чисел не существует квадратных корней из отрицательных чисел, поэтому потребовалось развивать теорию новых чисел, которые назвали комплексными. В рассмотрение ввели особое число, обозначаемое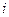 
и названное мнимой единицей, которое удовлетворяет следующему свойству:
.
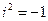Таким образом, выражение для корней квадратного уравнения, о которых писал Кардано, выглядит следующим образом: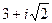 
и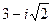 
. В дальнейшем ученые нашли очень простое геометрическое истолкование комплексных чисел. Если каждое действительное число есть точка на действительной оси, то каждому комплексному числу ставится в соответствие точка на координатной плоскости, называемой комплексной плоскостью.
В настоящее время комплексные числа применяются как математический аппарат электродинамики, квантовой механики и других наук.
Определение комплексного числа. Различные формы записи комплексного числа. Представление комплексных чисел на комплексной плоскости
Определение: комплексным числом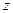 
называется упорядоченная пара 
действительных чисел. Число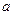 
называется действительной частью комплексного числа 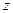, число 
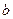называется мнимой частью комплексного числа .
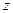Обозначения: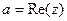 
, 
.
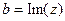Каждое комплексное число 
можно представить точкой на комплексной плоскости.
Комплексной плоскостью называют координатную плоскость (обозначают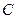 
), ось 
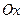которой называют действительной осью, ось 
называют мнимой осью. Единица действительной оси есть число 1, единица мнимой оси – мнимая единица 
.
Например, число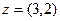 
можно представить точкой на комплексной плоскости (см. рис. 1), и отождествить с ней точку 
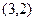на плоскости в декартовой системе координат.
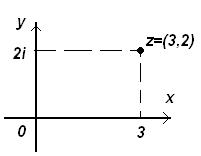
Рис. 1
Отметим, что комплексное число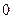 
записывается в виде 
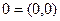, действительное число 1 есть комплексное число 
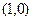, а мнимая единица записывается как 
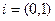. Поэтому
.
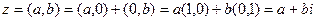Запись комплексного числа в виде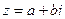 
называется алгебраической формой записи комплексного числа.
Определение: Числа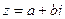 
и 
называются комплексно сопряженными.
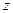Существует еще другая форма записи комплексного числа, которая называется тригонометрической. Рассмотрим на комплексной плоскости число . Соединим точку с точкой 0 и рассмотрим прямоугольный треугольник 
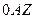(см. рис. 2).
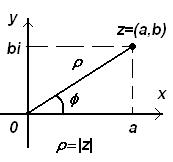
Рис. 2
Тогда, введя в рассмотрение угол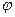 
и обозначив 
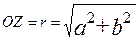, получим
, 
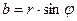и тогда 
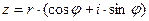называется тригонометрической формой записи комплексного числа.
называется модулем комплексного числа ,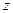
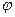называется аргументом комплексного числа 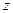и находится из системы равенств:
.
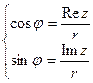Обозначения: 
, 
.
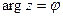Отметим свойства модуля и аргумента комплексного числа.
1. 
, причем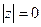 
, только если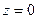 
2. 
равен расстоянию от точки z до точки 0 на комплексной плоскости (то есть, есть длина вектора на плоскости, соответствующего числу z)
3. если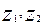 
- комплексные числа, то 
равен расстоянию между точками 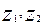на комплексной плоскости.
4. если числа 
- комплексно сопряженные, то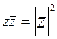 
5. 
, 
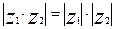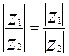
6. аргумент комплексного числа определен с точностью до числа 
Пример 1. Записать число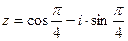 
в алгебраической и тригонометрической формах.
Решение. 1). Для того чтобы записать это число в алгебраической форме, вычислим:
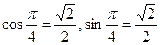. Подставив значения в число 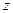, получим:
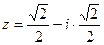- алгебраическая форма.
2). Нужно отметить, что число 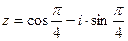записано не в тригонометрической форме, так как между действительной и мнимой частью стоит знак «минус». Учитывая, что функция 
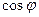-четная, а 
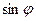- нечетная, имеем:
, 
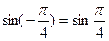, поэтому
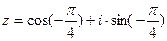- тригонометрическая форма.
Пример 2. Найти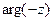 
.
Решение. Числа и 
симметричны относительно числа 0=(0,0) на комплексной плоскости. Поэтому вектор, соответствующий числу получается поворотом вектора на угол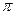 
против часовой стрелки вокруг точки 0. Поэтому 
.