НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Числовая последовательность. Предел последовательности.
Бесконечная числовая последовательность - это числовая функция, определенная на множестве N натуральных чисел.
Геометрически такая последовательность будет изображаться множеством точек. Числовая последовательность всегда бесконечна, но множество точек, которое они изображают, могут иметь как конечное, так и бесконечное число.
Например: Множество натуральных чисел: 
- геометр. представляют собой бесчисленное число различных точек.
Последовательность вида 
- бесконечна, но количество точек: две.
Различают последовательности:
- Возрастающие (убывающие) – xn+1 > xn (xn+1 < xn). Например:an=
- возраст. послед.; 
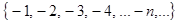- убыв. последовательность. - Ограниченные: сверху - xn £ M; снизу - xn ³ m; и сверху и снизу - m £ xn £ M. Например:
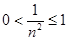
- Постоянные последовательности – это последовательность, все члены которой совпадают. Например:
.
Обычно последовательность задается формулой.
Например: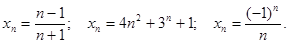 
Понятие о пределе последовательности
Число а называется пределом последовательности хn, если " e>0 все члены последовательности хn лежат в e-окрестности (а - e, а + e) т. а.
Т.е. найдется такой номер N£n, начиная с которого, отличие хn от а по модулю < e:
| хn – а| < e
Записывают:
(limit -предел (лат.))
Геометр.:
а-e а а+e
Последовательность может иметь один предел.
Последовательность называется бесконечно малой, если ее предел стремится к 0.
Например: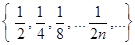 
® 0.
Последовательность называется бесконечно большой, если ее предел стремится к ¥.
Например: 
®¥.
Предел функции в точке
Число А называется пределом функции f(x) при х ® а, если " e>0, можно указать такое d>0, что для " x¹a удовлетворяющего неравенству 0<|x - a|<d, выполняется неравенство |f(x) – A|<e.
Записывают: 
Число А называется пределом f(X) при х®а, если по мере того, как х приближается к а (справа или слева), f(x) приближается к А.
Функция f(x) называется бесконечно малой при х®а, если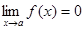 
.
Функция f(x) называется бесконечно большой при х®а, если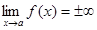 
.
Основные теоремы о бесконечно малых и бесконечно больших функциях
Т1. Если функции f(x) и g(x) – бесконечно малые (бесконечно большие), то также являются бесконечно малыми (бесконечно большими) функции:
1) f(x) + g(x) 2)f(x) · g(x) 3)kf(x), kÎR, k-const, k¹0
Т2. Произведение ограниченной переменной величины на бесконечно малую, также является бесконечно малой величиной.
Т3. Функция, обратная по величине бесконечно малой, есть бесконечно большая (и наоборот).
Основные теоремы о пределах
Т1. Если предел функции существует, то он единственный.
Т2. Предел постоянной величины, есть сама постоянная величина.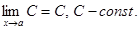 
Т3. Если $ пределы функций f(x) и g(x) при x®a, то $ также и предел их суммы (разности), равный сумме (разности) пределов f(x) и g(x):
Т4. Если $ пределы функций f(x) и g(x) при x®a, то $ также и предел их произведения, равный произведению пределов f(x) и g(x):
Следствие: Постоянный множитель можно вынести за скобку:
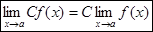
Т5. Если $ пределы функций f(x) и g(x) при x®a и предел g(x)¹0, то $ также предел отношения f(x)/ g(x), равный отношению пределов функций f(x) и g(x):
