Пример 1. При каких значениях параметра, а уравнение 2 cos2x – (2а + 9)cosx + 9а = 0 не имеет корней.
Решение. Пусть у = cosх, тогда исходное уравнение примет вид 2у2 – (2 а + 9)у + 9а = 0, корни которого у1 = а, у2 = 4,5. Уравнение cosх = 4,5 корней не имеет, а уравнение cosх = а не имеет корней, если 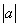 > 1.
> 1.
Ответ: (- 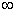 ; -1)
; -1) 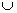 (1;
(1; 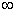 ).
).
Пример 2. Найдите все значения параметра а, при которых уравнение 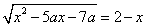 не имеет корней.
не имеет корней.
Решение. Данное уравнение равносильно системе: 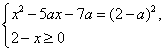

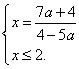 .
.
Уравнение не имеет решения в двух случаях: а = 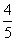 и
и 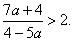
Ответ: 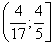 .
.
Пример 3. При каких значениях параметра а уравнение 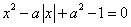 имеет единственное решение?
имеет единственное решение?
Решение. Решение уравнения может быть единственным только, если х = 0. Если х = 0,то а2 -1 = 0, и а = 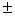 1.
1.
Рассмотрим 2 случая:
1) если а = 1, то х2 - 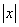 = 0 – корней три;
= 0 – корней три;
2). Если а = -1, то то х2 + 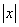 = 0, х = 0 - единственный корень.
= 0, х = 0 - единственный корень.
Пример 4. При каких значениях параметра а уравнение 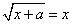 имеет 2 корня?
имеет 2 корня?
Решение. Данное уравнение равносильно системе:  . Выясним, когда квадратное уравнение х2 – х – а = 0 имеет 2 неотрицательных корня.
. Выясним, когда квадратное уравнение х2 – х – а = 0 имеет 2 неотрицательных корня.
Полученное уравнение имеет два корня, если 1+ 4а > 0; они неотрицательны, если

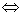 0 > а > -
0 > а > - 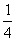 .
.
Ответ: (- 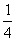 ; 0].
; 0].
Решение задач с параметрами может существенно облегчить использование графиков.
Пример. Решите уравнение в зависимости от параметра а: 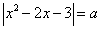 .
.
Решение. Понятно что при а 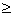 0:
0:
 .
.
Все ли корни подходят. Чтобы это выяснить, построим график функции а = 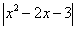 .
.
Количество корней можно увидеть на рисунке:
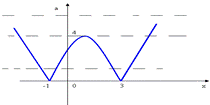
- если а < 0, то корней нет;
- если а = 0 и а > 0, то 2 корня.
Найдем эти корни.
При а = 0 получим х2 – 2х – 3 = 0 и х1 = -1, х2 = 3; при а > 4 это корни уравнения х2 – 2х – 3 – а = 0.
Если 0< а < 4 – все 4 корня подходят.
Если а = 4 – три корня: 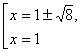
Ответ: 1) если а < 0, то корней нет;
2) если а = 0, то х1 = -1, х2 =3;
3) если 0 < a < 4, то х1,2,3.4 = 1 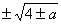 ;
;
4) если а = 4, то х1 = 1; х2,3 = 1 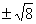 ;
;
5) если а > 4, то х1,2 = 1 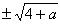 .
.
Решим неравенства
Пример 1
Найти все значения параметра а, при каждом из которых для любого значения х выполняется неравенство
│3sin2x + 2asinx ∙ cosx + cos2x + a│≤ 3,
Решение:
Заданное неравенство эквивалентно системе неравенств
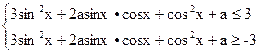
Используя тождество sin2 + cos2 =1, запишем систему в виде
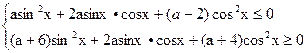
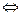
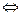
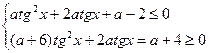
Последняя система имеет решение для любого х, если
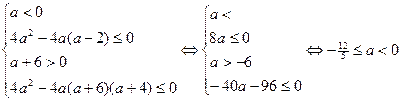
Если а = 0, то система также разрешима для любого х.
Ответ: 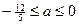
Пример 2
Найти наибольшее значение параметра b, при котором неравенство
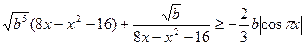
имеет хотя бы одно решение.
Решение:
При b< 0 неравенство не имеет смысла.
При b=0 неравенство верно при всех допустимых значениях х
Рассмотрим случай b >0.
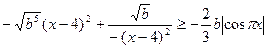
Умножим обе части неравенства на -1, получим
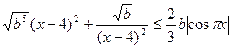
Так как b >0, разделим обе части неравенства на b
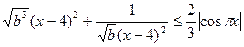
Заметим, что выражение в правой части принимает значения от 0 до 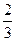 .
.
Оценим выражение в левой части неравенства.
Пусть 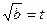 , (х-4)2 = а. Рассмотрим функцию f(a) =
, (х-4)2 = а. Рассмотрим функцию f(a) = 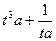 , a ≠ 0
, a ≠ 0
f '(a) = 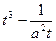 . Найдем точки, в которых производная равна 0.
. Найдем точки, в которых производная равна 0.
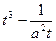 = 0
= 0
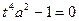
a = 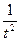
 Следовательно, a =
Следовательно, a = 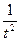 является точкой минимума функции.
является точкой минимума функции.
f(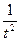 ) =
) = 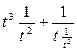 = 2t.
= 2t.
Так как, выражение в правой части принимает значения от 0 до 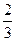 , то исходное неравенство имеет хотя бы одно решение при 0 < 2t ≤
, то исходное неравенство имеет хотя бы одно решение при 0 < 2t ≤ 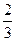 , а наибольшее значение выражение 2t принимает в случае равенства
, а наибольшее значение выражение 2t принимает в случае равенства 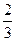 .
.
2t = 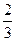 t =
t = 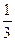
Так как 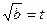 , b =
, b = 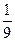 .
.
Ответ: 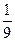
Тестовый контроль
| 1 вариант | 2 вариант |
1) Решите уравнение: 0 · х = а
Ответы: а) при а ≠ 0, х = 1, при а = 0, х  R
б) при а = 0, х R
б) при а = 0, х 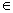 R, при а ≠ 0 корней нет
в) при а = 0 нет корней, при а ≠ х = R, при а ≠ 0 корней нет
в) при а = 0 нет корней, при а ≠ х = 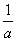
| 1) Решить уравнение: а х = а.
Ответы: а) при а ≠ 0, х = 1, при а = 0, х 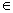 R
б) при а = 0, х R
б) при а = 0, х 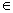 R, при а ≠ 0 корней нет
в) при а = 0 нет корней, при а ≠ х = R, при а ≠ 0 корней нет
в) при а = 0 нет корней, при а ≠ х = 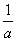
|
2) Решит уравнение: (в – 2)·х = 5 + в.
Ответы:
а) при в = 2 нет корней; при в ≠2, х = 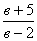 ;
б) при в = -2 нет корней, при в ≠-2 х = ;
б) при в = -2 нет корней, при в ≠-2 х = 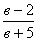 в) при в = -1 нет корней, при а ≠ - 1
в) при в = -1 нет корней, при а ≠ - 1 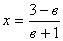
| 2) Решите уравнение (в + 1)·х = 3 – в.
Ответы:
а) при в = 2 нет корней; при в ≠2, х = 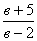 ;
б) при в = -2 нет корней, при в ≠-2 х = ;
б) при в = -2 нет корней, при в ≠-2 х = 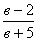 в) при в = -1 нет корней, при а ≠ - 1
в) при в = -1 нет корней, при а ≠ - 1 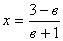
|
3) При каких значениях параметра с уравнение имеет бесконечное множество решений?
с·(с + 1)·х = с2 – 1.
Ответ: а) при с = -1, х 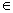 R,
б) при с = 2, х R,
б) при с = 2, х 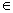 R,
в) при с = - 1, х R,
в) при с = - 1, х 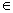 R, R,
| 3) При каких значениях параметра с уравнение имеет бесконечное множество решений?
(с2 – 4)·х = (с – 2)·(с+ 1).
Ответ: а) при с = -1, х 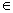 R,
б) при с = 2, х R,
б) при с = 2, х 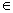 R,
в) при с = - 1, х R,
в) при с = - 1, х 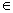 R, R,
|
4) При каких значениях параметра m уравнения не имеет решений?
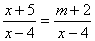 .
Ответы: а) при m = 6 нет корней;
б) при m = 7 нет корней;
в) при m = 8 нет корней. .
Ответы: а) при m = 6 нет корней;
б) при m = 7 нет корней;
в) при m = 8 нет корней.
| 4) При каких значениях параметра m уравнения не имеет решений?
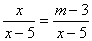 .
Ответы: а) при m = 6 нет корней;
б) при m = 7 нет корней;
в) при m = 8 нет корней. .
Ответы: а) при m = 6 нет корней;
б) при m = 7 нет корней;
в) при m = 8 нет корней.
|
5) Решить уравнение 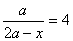 .
Ответы:
а) при а = 0 нет корней, при а ≠ 0 х = .
Ответы:
а) при а = 0 нет корней, при а ≠ 0 х =  ;
б) при а = 0 нет корней, при а ≠ 0 х = ;
б) при а = 0 нет корней, при а ≠ 0 х = 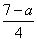 ;
в) при а = 0 нет корней, а ≠ 0 х = - 2а. ;
в) при а = 0 нет корней, а ≠ 0 х = - 2а.
| 5) Решить уравнение 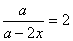 .
Ответы:
а) при а = 0 нет корней, при а ≠ 0 х = .
Ответы:
а) при а = 0 нет корней, при а ≠ 0 х =  ;
б) при а = 0 нет корней, при а ≠ 0 х = ;
б) при а = 0 нет корней, при а ≠ 0 х =  ;
в) при а = 0 нет корней, а ≠ 0 х = - 2а. ;
в) при а = 0 нет корней, а ≠ 0 х = - 2а.
|
6) При каких значениях параметра n уравнение имеет один корень?
nх2 + 4х + (5 – n) = 0.
Ответы:
а) при n = 0 х =1, при n = 2 х = 2, при n =2 х = 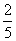 ;
б) при n = 0 х = - ;
б) при n = 0 х = - 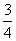 , при n = 1 х = 2, при n = - 4 х = , при n = 1 х = 2, при n = - 4 х = 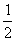 ;
в) при n= 0 х = - ;
в) при n= 0 х = - 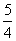 , при n = 1 х = - 2, при n =4 х = - , при n = 1 х = - 2, при n =4 х = - 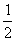 . .
| 6) При каких значениях параметра n уравнение имеет один корень?
nх2 + 4х + (3 + n) = 0.
Ответы:
а) при n = 0 х =1, при n = 2 х = 2, при n =2 х = 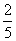 ;
б) при n = 0 х = - ;
б) при n = 0 х = - 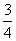 , при n = 1 х = 2, при n = - 4 х = , при n = 1 х = 2, при n = - 4 х = 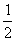 ;
в) при n= 0 х = - ;
в) при n= 0 х = - 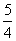 , при n = 1 х = - 2, при n =4 х = - , при n = 1 х = - 2, при n =4 х = - 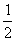 . .
|