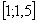Рассмотрим примеры решения задач с параметрами 2 типа.

Задание: изучить материал урока и письменно пройти тестовый контроль.

Урок

Тема: Исследование уравнений и неравенств с параметром.

Цель: формировать умения и навыки по решению задач с параметрами

Ход урока.

1. Изучение нового материала

Теоретический минимум

Задача с параметром – это множество задач, каждая из которых получается из условия подстановкой конкретного значения параметра.

Область допустимых значений параметра – это множество значений параметра, при подстановке которых получается задача, имеющая смысл.

Решить задачу с параметром означает для любого допустимого значения параметра найти множество всех решений данной задачи.

Рассматривать мы с вами будем задачи с параметром двух основных типов.

В задачах I типа требуется для каждого значения параметра решить задачу.

Для этого необходимо:

• разбить ОДЗ параметра на части, на каждой из которых задачу можно решить одним и тем же способом;
• на каждой из полученных частей решить задачу.

В задачах II типа требуется найти все значения параметра, при которых выполнены те или иные заданные условия.

Ответ в задаче с параметром – это описание множества ответов к задачам, полученных при конкретных значениях параметра.

Решение задач.

1) Решить уравнение а (а – 1) = а – 1.

Решение. Перед нами линейное уравнение, имеющее смысл при всех допустимых значениях а. Будем решать его «как обычно»: делим обе части уравнения на коэффициент при неизвестном. Но всегда ли возможно деление?

Нет.

Делить на ноль нельзя. Придется рассмотреть отдельно случай, когда коэффициент при неизвестном равен о. Получим:

1. а = 1, тогда уравнение примет вид 0·х = 0, где х – любое число;
2. а = 0, тогда 0∙х = - 1 – уравнение корней не имеет;

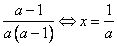1. а 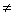0, а 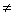1, тогда а (а – 1)·х = а – 1 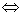х =

Ответ: 1) если 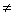а 0, а 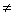1, то х = ;

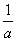2) если а = 1, то х – любое число;

3) если а = 0, то корней нет.

2) Решить уравнение (а – 1)х² + 2 (2а – 1)х + 4 а + 3 = 0.

Решение. Рассмотрим два случая:

1. а = 1 – получим линейное уравнение 2х + 7 = 0, откуда х = - 3,5;
2. а 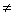1 – получим квадратное уравнение.

Рассмотрим дискриминант: D = (2а – 1) ² – (а – 1)(4а + 3) = - 3а + 4.

Далее, если а > 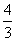, то D < 0 и уравнение корней не имеет.

Если же а 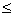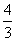, то х_1,2 = .

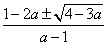Ответ: 1) если а > 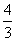, то корней нет;

2) если а = 1, то х = - 3,5;

3) есл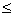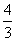и а и а 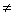1, то х_1,2 = .

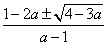Рассмотрим примеры решения задач с параметрами 2 типа.

Особенно часто встречаются задачи на расположение корней квадратного уравнения. При их решении хорошо «работают» графические иллюстрации. Расположение корней относительно заданных точек плоскостью определяется направлением ветвей соответствующей параболы, координатами вершины, а также значениями в заданных точках.

Примеры:

1) При каких значениях параметра а уравнение (а² + а + 1)х² + (2а – 3)х + а – 5 = 0 имеет два корня, один из которых больше 1, а другой меньше 1?

Решение. Пусть f(х) = (а² + а + 1)х² + (2а – 3)х + а – 5. Так как а² + а + 1 >0, то для квадратичной функции f(х) условие задачи может выполняться только при условии f (х) < 0.

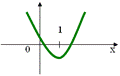
Решая неравенство f(1) = а² + 4а – 7 < 0, получим, что -2 - 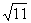< а < - 2 + .

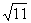Ответ: -2 - 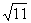< а < - 2 + .

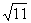2) При каких значениях параметра m корни уравнения (m – 1)х² – 2mх + m + 3 = 0 положительны?

Решение. Пусть f(х) = (m-1)х² - 2 mх + m + 3 тогда:

1) если, m = 1,то -2х + 4=0, х= 2- корень положителен;

2) если m 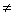1, то с помощью рисунка можно получить следующие соотношения:

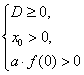
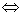
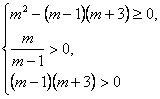
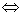
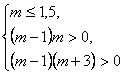
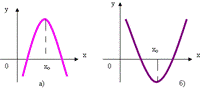
Рассмотрим 2 случая:

1) если 1,5 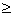m > 0, тогда из 2 и 3 неравенств последней системы получим, что m > 1, т.е. окончательно 1,5 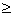m > 1;

2) если m < 0, тогда из неравенства (m-1)m > 0 получим, что m-1 < 0, откуда m + 3 < 0, т.е. окончательно m < -3.

Ответ: m 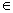(- 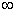; -3)