Подбор поперечного сечения по нормальным напряжениям

 

 

Условие прочности:

Абсолютная величина максимального изгибающего момента равна 41,32 кН.м. Тогданеобходимый момент сопротивления

Максимальный изгибающий момент с М(х)

Момент сопротивления для прямоугольного сечения: .

Из условия прочности

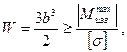откуда

 

III- Задача 3

Построим эпюры Q и M для консольной балки,при , , ,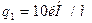

 

 

Расчетная схема

 

 

 

Найдем Q и М

Определяем реакций опор

Для определения Q и M в любом сечении балки необходимо знать все внешние силы, действующие на балку, т.е. приложенные нагрузки и опорные реакции.

 

Определим неизвестные реакции опор, используя уравнения равновесия статики:

 

 

 

 

Для проверки составим уравнение статики, не использованное при расчете реакций, например, сумму проекций всех сил на ось Y:

 

а) На первом участке x₁ изменяется в пределах . Перерезывающая сила на первом участке постоянна: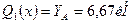

Изгибающий момент на этом участке изменяется линейно: ;

 

б) На втором участке x₂ изменяется в пределах . Перерезывающая сила на втором изменяется линейно:

 

Изгибающий момент на этом участке изменяется по линий: ;

 

в) На третьем участке x₃ изменяется в пределах . Перерезывающая сила на третьем участке изменяется линейно: ,

Изгибающий момент на этом участке изменяется по параболе:

 

- Парабола

Для уточнения вида эпюры M на первом участке необходимо исследовать выражение на максимум:

Отсюда определяем то значение , при котором

 

Поставив это значение в выражение 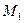, найдем

 

 

Построение эпюра

 

 

В) Опасная нагрузка и опасное сечение

Опасная нагрузка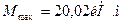

Опасное сечение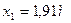

 

Подбор поперечного сечения по нормальным напряжениям

Абсолютная величина максимального изгибающего момента равна 20кН.м. Тогданеобходимый момент сопротивления

Исходя из таблицы стандартов ГОСТ 8239-89, выбираем двутавр № 18 (). И № 16 с моментом сопротивления, несколько больше требуемого (:

 

Недонапряжение материала составляет .

Выбираем двутавр № 16 с моментом сопротивления меньшим требуемого .

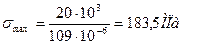
Перенапряжение материала составляет , что не допустимо.

Окончательно выбираем двутавр № 18.

Задача 4

Построим эпюры Q и M для консольной балки,при , , ,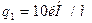

 

Расчетная схема

 

 

 

Найдем Q, M?

 

Определяем реакций опор

 

Для определения Q и M в любом сечении балки необходимо знать все внешние силы, действующие на балку, т.е. приложенные нагрузки и опорные реакции.

Статика позволяет написать только 3 уравнения равновесия. Четвертое уравнение составим из условия, что шарнир С по свойству конструкции не может передать момента, так как не препятствует повороту одной части балки АС относительно другой СВ. Следовательно, сумма моментов относительно точки С сил, приложенных слева или справа от шарнира, равняется нулю.

Составим уравнения статики и дополнительное уравнение:

 

 

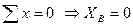
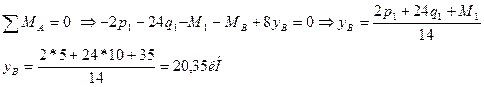
Для проверки составим уравнение статики, не использованное при расчете реакций, например, сумму проекций всех сил на ось Y:

 

a) На первом участке x₁ изменяется в пределах . Перерезывающая сила на первом участке: .

Изгибающий момент на этом участке Парабола

 

 

Б) На втором участке x₂ изменяется в пределах 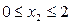. Перерезывающая сила на втором участке постоянна: .

 

Изгибающий момент на этом участке изменяется линейно:

 

 

В)На третьем участке x₃ изменяется в пределах . Перерезывающая сила на третьем участке изменяется постоянно: ,.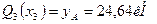

Изгибающий момент на этом участке изменяется по параболе: ; где и

 

Построение эпюра Q и М