Тема 4 1.4. Модели оптимизации конструкций (2 ч.)

В общем случае в теории проектирования объектом исследования является модели проектных ситуаций, в которых выделяются:

1. Задание на проект, в который входит назначение конструкции и условия эксплуатации;

2. Средства определения оптимума, в которые входят свойства конструкционных материалов, различные ограничения, технология изготовления изделия, методы оптимизации;

3. Технико-экономические показатели проекта (затраты на изготовление и эксплуатации изделия).

Здесь рассматриваются методы проектирования оптимальных по массе конструкций с учетом конструктивно-технологических особенностей. Модели оптимизации можно отнести к 2 классам:

Первый класс основан на параметрическом методе оптимизации варьируемых параметров (конструктивный метод оптимизации). Искомые параметры рассматриваются как искомые величины, то есть являются константами, которые дают оптимум конструкции при определенном числовом их сочетании. В этом случае поиск оптимума сводится к анализу и упорядочению однозначно определенных моделей оптимального множества точек конечномерного вещественного пространства.

Во втором классе задач проектируются варьируемые параметры, которые все или часть из них являются функциями координат или изменяемыми функциями. В общем случае они носят кусочно-гладкий характер. Такие модели называются моделями оптимального управления. За некоторым исключением эти задачи очень сложны для реализации и решаются только численно. Математическая теория оптимального управления в основном использует принцип максимума Понтрягина и метод динамического программирования Беллмана. Оба эти метода не имеют аналитического решения и могут решаться только численно.

В принципе Понтрягина решение сводится к краевой задаче, в разрешающей системе которой содержится в 2 раза больше дифференциальных уравнений, чем в исходной задаче, за счет того, что рассматривается два момента времени или два состояния. В методе Беллмана оптимизация сводится к решению нелинейного дифференциального уравнения в частных производных очень высокого порядка.

Оптимальное проектирование конструкций из КМ осуществляется чаще всего численно сведением задачи к условному экстремуму с использованием аналитического подхода, если это возможно, или на основе метода математического программирования. Существует достаточное количество конструктивных методов оптимизации. Рассмотрим некоторые из них.

Конструктивные критерии оптимизации получили широкое распространение из-за их относительной простоты. При этом предполагается, что конструкция минимальной массы должна обладать некоторыми свойствами, реализация которых предусмотрена критерием оптимальности. Такие критерии, как правило, не соответствуют строго критерию минимума массы.

Наиболее известным и простым является критерий равнопрочности. Согласно ему из всех конструкций, воспринимающих данную нагрузку и изготовленных из заданного материала, минимальной массой обладает та, для которой напряженное состояние в каждой точке принадлежит поверхности разрушения s _в= s_i, где s_i – обобщенное напряжение. Наиболее просто это условие реализуемо для статически определимых конструкций, к которым относятся стержневые системы и безмоментные оболочки. Доказательство достаточности условия равнопрочности для одноосного состояния (растяжение или сжатие) и его эффективность обусловлена тем, что оно непосредственно записывается через параметры, определяющие напряженное состояние (НС) конструкции. При сложном НС условие равнопрочности не всегда гарантирует минимум массы, т.к. НС разных точек конструкций может соответствовать разным точкам на поверхности прочности. Рассмотрим пример выполнения условия равнопрочности на примере баллона давления из композиционного материала (рис.1.2). Для нитяной структуры без учета связующего волокнистый материал конструкции можно считать близким к стержневым системам, если число слоев, уложенных под разными углами, не превышает трех.

Введем обозначения (рис.1.2): a – продольная координата; b – окружная координата; p – внутреннее давление; R – средний радиус оболочки; h _c – толщина спирального слоя, с углом укладки слоев ± j; h _k – толщина кольцевого слоя, с углом укладки j =90⁰. Структуру материала рассчитываем без учета связующего (нитяная структура). Оболочку считаем безмоментной. Тогда суммарные усилия в обшивке N _a и N _b равны: N _a= pR /2; N _b = pR. Проекции напряжений в слоях на направления a и b дают усилия N _a и N _b соответственно N _a= s _1с h _ccos² j, N _b= s _1с h _csin² j + s _1k h _k. С учетом выражения N _a и N _b через величину давления можно определить напряжения в спиральном и кольцевом слоях в виде

; .

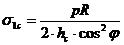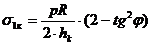Для равнопрочной конструкции, когда напряжения во всех слоях одинаковы, можем принять s _1с= s _1k= s _в. Суммарная толщина оболочки равна h = h _k+ h _c и должна быть минимальной. Тогда масса цилиндрической части баллона вычисляется по формуле G = 2pRL(h_c + h_k)ρ и в этом случае будет минимальной. Где R - радиус оболочки, L - длина оболочки, ρ - плотность материала. Так как масса не зависит от углов укладки, то и толщина не должна зависеть от углов укладки волокон. В случае, когда напряжения в слоях достигают величины предела прочности 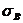, то толщины слоев будут минимальны и равны

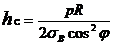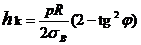, , (1.5)

а суммарная толщина не зависит от углов укладки слоев и равна

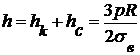. (1.6)

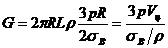
Для определения весового совершенства цилиндрической части баллона перепишем его массу через его объем V _ц:

, (V _ц = 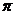R ² L и h _c 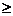0, h _k 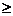0).

Рассмотрим случай когда h _k=0, тогда из условия (1.5) имеем 2 – tg² j ³ 0 или tg j £ 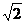. Следовательно, угол укладки, обеспечивающий равновесие цилиндрической оболочке одним семейством нитей от внутреннего давления, равен j £ 54⁰44 ^’ и радиус отверстия равен радиусу цилиндра. При j < 54⁰44’ диаметр отверстия d начинает уменьшаться. При j =0, d =0 волокна переходят через полюс днища, что невозможно реализовать. Для равнопрочного баллона формула определения массы справедлива для любой формы оболочки. Для цилиндрического баллона она имеет вид

.

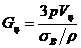
Для сферического баллона при равенстве усилий: 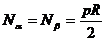толщина оболочки равна h _сф= pR /2. Тогда масса сферического баллона с учетом величины площади ее поверхности и толщины равна 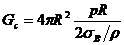. Это же выражение можно записать, используя формулу объема сферы 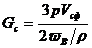. Если принять, что объемы цилиндрического и сферического баллонов одинаковы, то оказывается, что масса сферического баллона в два раза меньше.

Сравним массы одинаковых по форме и объему стальных и пластиковых баллонов, имеющие следующие характеристики:

- стальной баллон: s _b = 1800 МПа, ρ = 7800 кг/м³;

- баллон из стеклопластика: s _b=1800 МПа; ρ =1800кг/м³.

Тогда отношение масс стального и пластикового баллонов равно 2,1. Если при проектировании баллона учитывать связующее, то должны использоваться критерии прочности с учетом напряжений s ₁, s ₂, t ₁₂.

Существуют и другие конструктивные критерии для проектирования конструкции. К ним, например, можно отнести критерий минимума потенциальной энергии деформации при заданной системе нагрузок. Этот критерий, эквивалентен условию постоянства удельной энергии деформации в каждой точке конструкции, и определяет конструкцию максимальной жесткости. Определение параметров из условия минимума потенциальной энергии эквивалентно построению равнопрочной конструкции, если условие прочности материала записывается через полную удельную энергию деформации. Большинство существующих критериев предполагает упругость материала вплоть до разрушения и не учитывают наличие пластичности. Учет реальной диаграммы деформирования материала достаточно сложен даже при прямом расчете конструкции. Решение существенно упрощается, если материал считается идеально пластичным.