С вероятностью 0,954 можно утверждать, что средняя масса изделия всей партии изготовленных изделий колеблется в пределах от 3174,74 г. до 3197,76 г.

Задание 1

 

За отчетный период работа заводов, выпускающих одноименную продукцию, характеризуется следующими данными

 

№ завода	Фактически произведено продукции, тыс. шт.	Общая сумма затрат на производство продукции, млн. руб.
	10,6	61,8
	6,4	39,7
	4,6	39,8
	10,7	62,6
	4,7	29,1
	9,4	55,3
	4,0	26,4
	6,7	41,6
	11,8	64,9
	3,9	28,5
	4,2	28,6
	4,3	28,8
	3,9	24,9
	5,0	36,6
	10,1	57,0
	11,3	67,2
	3,0	22,2
	2,6	19,0
	8,0	48,0
	6,7	41,9
	6,0	40,9
	1,8	13,3
	7,1	44,7
	6,3	40,3
	8,4	49,6
	9,0	58,6
	8,8	54,6
	5,9	34,1
	6,2	38,4
	7,0	42,9

С целью выявления зависимости между объемом произведенной продукции и ее себестоимостью произведите аналитическую группировку по объему произведенной продукции, образовав 5 групп заводов с равными интервалами. По каждой группе и в целом посчитайте число заводов, объем произведенной продукции всего и в среднем на один завод, общую сумму затрат на производство продукции, себестоимость единицы продукции. Составить групповую таблицу, сделать краткие выводы.

Решение

Строим ранжированный ряд заводов по величине объема произведенной продукции.

 

Ранг	Фактически произведено продукции, тыс. шт.	Общая сумма затрат на производство продукции, млн. руб.	№ завода
	1,8	13,3
	2,6
		22,2
	3,9	24,9
	3,9	28,5
		26,4
	4,2	28,6
	4,3	28,8
	4,6	39,8
	4,7	29,1
		36,6
	5,9	34,1
		40,9
	6,2	38,4
	6,3	40,3
	6,4	39,7
	6,7	41,9
	6,7	41,6
		42,9
	7,1	44,7
	8,4	49,6
	8,8	54,6
		58,6
	9,4	55,3
	10,1	57,0
	10,6	61,8
	10,7	62,6
	11,3	67,2
	11,8	64,9

 

При n = 5 получаем размер интервала

 

= (11,8-1,8)/=2.

 

Номер группы	Фактически произведено продукции, тыс. шт.
	1,8-3,8
	3,8-5,8
	5,8-7,8
	7,8-9,8
	9,8-11,8

 

Составим разработочную таблицу

 

Группа	Номер завода	Фактически произведено продукции, тыс. шт.	Общая сумма затрат на производство продукции, млн. руб.
1 (1,8-3,8)		1,8	13,3
	2,6
		22,2
2 (3,8-5,8)		3,9	24,9
	3,9	28,5
		26,4
	4,2	28,6
	4,3	28,8
	4,6	39,8
	4,7	29,1
		36,6
3 (5,8-7,8)		5,9	34,1
		40,9
	6,2	38,4
	6,3	40,3
	6,4	39,7
	6,7	41,9
	6,7	41,6
		42,9
	7,1	44,7
4 (7,8-9,8)
	8,4	49.6
	8,8	54.6
		58.6
	9,4	55.3
5 (9,8-11,8)		10,1
	10,6	61.8
	10,7	62.6
	11,3	67.2
	11,8	64.9

 

Составим конечную аналитическую таблицу

 

Группа	Количество заводов	Фактически произведено продукции, тыс. шт.	Общая сумма затрат на производство продукции, млн. руб.
в целом	в среднем на 1 завод	в целом	в среднем на 1 завод
1 (1,8-3,8)		7,4	2,47	54,5	18,17
2(3,8-5,8)		34,6	4,325	242,7	30,338
3(5,8-7,8)		58,3	6,48	364,5	40,5
4 (7,8-9,8)		43.6	8.72	266.1	53.22
5 (9,8-11,8)		54.5	10.9	313.5	62.7
Итого		198.4	-	819,3	-

 

Таким образом, данные этой таблицы будут представлять искомую аналитическую группировку. По ней делаем выводы. Группировка показала наличие прямой зависимости между объемом фактически произведенной продукции и общей суммой затрат на производство продукции: с ростом значений факторного признака растут значения результативного признака.

Задание 2

 

Имеются данные об урожайности и посевной площади зерновых культур в колхозе

 

№ бригады	Базисный период	Отчетный период
Урожайность, ц/га	Посевная площадь, га	Урожайность, ц/га	Валовой сбор, ц

 

Требуется исчислить среднюю урожайность пшеницы в базисном и отчетном периоде.

Указать, какие виды средних применялись.

Решение

Средняя урожайность зерновых с одного гектара в хозяйстве за базисный период составила:

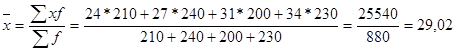ц с га.

Мы применили формулу средней арифметической взвешенной, так как имеются данные первичных значений признака и числа единиц совокупности.

Средняя урожайность зерновых с одного гектара в хозяйстве в отчетном периоде составила:

ц с га

Мы применили формулу средней гармонической, так как известны не первичные, а вторичные носители признака, и отсутствуют данные о частотах.

 

Задание 3

 

При выборочном обследовании 0,5% партии кирпича установлено, что из обследованных 400 образцов 80 отнесены к нестандартной продукции, а распределение выборочной совокупности по весу следующее:

 

Вес изделия, г.	Число образцов, шт.
До 3000
3000-3100
3100-3200
3200-3300
Свыше 3300
Итого

 

По этим данным определите для всей партии продукции:

1. С вероятностью 0,954 возможные границы, в которых ожидается средняя масса изделия всей партии изготовленных изделий.

2. С вероятностью 0,997 возможные пределы удельного веса стандартной продукции.

Указания:

1. Обследование проведено по схеме случайной бесповторной выборки.

2. При расчете среднего веса одного образца в выборке и среднего квадратического отклонения надо использовать способ моментов. Величина открытого интервала условно приравнивается к величине интервала закрытого.

Решение

1. Для нахождения среднего значения признака необходимо преобразовать интервальный ряд в дискретный, вычислив центр интервала в каждой группе:

 

Вес изделия, г.	Число образцов, шт.	Вес изделий всех образцов, г.
Итого

Средний вес изделия:

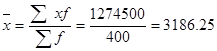г.

 

Расчет среднего квадратического отклонения проведем на основе составленной вспомогательной таблицы:

 

Вес изделия, г.	Число образцов, шт.	Вес изделий всех образцов, г.	x-	(x- )2	(x- )2f
			-236.25	55814.0625	1395351.5625
			-136.25	18564.0625	1206664.0625
			-36.25	1314.0625	170828.125
			63.75	4064.0625	406406.25
			163.75	26814.0625
Итого			-	-

 

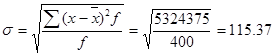г.

г.

Вычислим пределы среднего веса изделия:

3186,25-11,51≤ ≤3186,25+11,51

3174,74≤ ≤3197,76

 

С вероятностью 0,954 можно утверждать, что средняя масса изделия всей партии изготовленных изделий колеблется в пределах от 3174,74 г. до 3197,76 г.