RSA-шифрование сообщения  выполняется с помощью открытого ключа получателя
выполняется с помощью открытого ключа получателя  по формуле
по формуле
 ,
,
где  и
и  числовые эквиваленты символов исходного и зашифрованного сообщений.
числовые эквиваленты символов исходного и зашифрованного сообщений.
RSA-дешифрирование зашифрованного сообщения 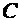 выполняется с помощью закрытого ключа
выполняется с помощью закрытого ключа  получателя по формуле
получателя по формуле
 .
.
Рассмотрим пример шифрования RSA на малых числах, чтобы можно было проверить его работу на калькуляторе. Зашифруем сообщение «ДВГУПС» с помощью открытого ключа (5, 91) (рис. 6). В результате получим шифрограмму «31, 61, 23, 21, 75, 80».
Символы исходного сообщения, 
| Коды символов  , табл. 3 , табл. 3
| Зашифрованные коды символов, 
|
| Д | 55 mod 91 = 31 | |
| В | 35 mod 91 = 61 | |
| Г | 45 mod 91 = 23 | |
| У | 215 mod 91 = 21 | |
| П | 175 mod 91 = 75 | |
| С | 195 mod 91 = 80 |
Рис. 6. Шифрование RSA
Дешифрируем шифрограмму «31, 61, 23, 21, 75, 80» закрытым ключом (29, 91), рис. 7. В результате получим исходное сообщение «ДВГУПС».
Коды шифрограммы, 
| Дешифрированные коды символов 
| Исходный текст 
|
| 3129 mod 91 = 5 | Д | |
| 6129 mod 91 = 3 | В | |
| 2329 mod 91 = 4 | Г | |
| 2129 mod 91 = 21 | У | |
| 7529 mod 91 = 17 | П | |
| 8029 mod 91 = 19 | С |
Рис. 7. Дешифрирование RSA
Задание 7. Создайте открытый и закрытый ключи при заданных в вашем варианте  и
и  (табл. 6 приложения). В качестве числа
(табл. 6 приложения). В качестве числа  , входящего в состав открытого ключа, возьмите наибольшее простое число, меньшее
, входящего в состав открытого ключа, возьмите наибольшее простое число, меньшее  , см. таблицу простых чисел (табл. 4).
, см. таблицу простых чисел (табл. 4).
Задание 8. Используя алфавит из 44 символов (33 русские буквы, пробел и 10 цифр, табл. 3), зашифруйте сообщение с помощью созданного Вами открытого ключа. Сообщение выбирается по варианту из
табл. 6 приложения.
Задание 9. Дешифрируйте шифрограмму с помощью созданного Вами в задании 7 закрытого ключа. Шифрограмма выбирается по варианту из табл. 7 приложения.
Электронная подпись
Ассиметричная криптография позволяет любому пользователю зашифровать своё сообщение открытым ключом получателя. Но остаётся угроза подмены сообщения третьим лицом (злоумышленником). Для защиты от этого была предложена в 1976 г. У. Диффи и М. Хелманом идея электронной подписи, вычисляемой на основе закрытого ключа отправителя и проверяемой открытым ключом отправителя. Таким образом, только отправитель может поставить свою подпись, и в то же время любой желающий может удостовериться, что это именно его подпись.
Электронная подпись (ЭП) – это присоединяемое к сообщению его криптографическое преобразование (хеш-образ), которое позволяет при получении проверить авторство и подлинность сообщения. ЭП содержит зашифрованные сведения о передаваемом сообщении и его авторе. При этом электронная подпись надёжнее решает не только традиционные задачи авторства и подлинности документа, которые ранее обеспечивались рукописной подписью под бумажным документом, но и следующие важные задачи электронного документооборота:
– целостность документа;
– невозможность подделки подписи;
– предотвращение отказа от подписи;
– юридическая значимость документа.
Вычисление ЭП
Алгоритм ЭП начинается с предварительного хеширования сообщения – вычисляется значение некоторой контрольной функции от всего сообщения. Для вычисления хеш-образа 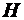 сообщения
сообщения  в данной работе предлагается использовать упрощённую хеш-функцию квадратичной свёртки
в данной работе предлагается использовать упрощённую хеш-функцию квадратичной свёртки
 , (1)
, (1)
где  ,
,  из открытого ключа автора сообщения,
из открытого ключа автора сообщения,  – коды символов сообщения, открытого или предварительно зашифрованного. После обработки последнего символа получаем хеш-образ всего сообщения
– коды символов сообщения, открытого или предварительно зашифрованного. После обработки последнего символа получаем хеш-образ всего сообщения 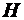 .
.
В алгоритмах ЭП назначение открытого и закрытого ключей меняются – сообщение подписывается закрытым ключом отправителя, после чего любой может проверить подлинность с помощью открытого ключа отправителя. Вычисление электронной электронной подписи  проводится по хеш-образу
проводится по хеш-образу 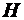 пересылаемого сообщения
пересылаемого сообщения  с помощью закрытого ключа
с помощью закрытого ключа 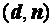 автора сообщения по формуле
автора сообщения по формуле
 . (2)
. (2)
Формирование сообщения, подписанного ЭП, для передачи осуществляется присоединением ЭП  к сообщению
к сообщению  :
:
 .
.
Например, поставим электронную подпись на сообщение «МАША » с помощью закрытого ключа отправителя 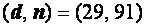 . Для этого вычислим хеш-образ сообщения (рис. 8).
. Для этого вычислим хеш-образ сообщения (рис. 8).

| Символы исходного сообщения 
| Коды символов 
| Вычисление хеш-образа
|

| |||
| М | 
| ||
| А | 
| ||
| Ш | 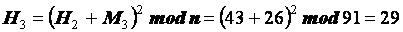
| ||
| А | 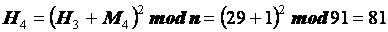
| ||
| Хеш-образ | 
| ||
| Электронная подпись | 
|
Рис. 8. Вычисление ЭП
Хеш-образом 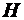 отправляемого сообщения «МАША » является число 81. Вычисление ЭП
отправляемого сообщения «МАША » является число 81. Вычисление ЭП  по хеш-образу с помощью закрытого ключа отправителя производится по формуле (2). Электронной подписью сообщения является число 9. Сформируем сообщение для передачи, добавив к нему ЭП. Получим «9МАША ».
по хеш-образу с помощью закрытого ключа отправителя производится по формуле (2). Электронной подписью сообщения является число 9. Сформируем сообщение для передачи, добавив к нему ЭП. Получим «9МАША ».
Проверка подлинности ЭП
Процедура проверки подлинности ЭП и самого сообщения заключается в следующем..
1. Отделяется ЭП от основного сообщения.
2. Выделяется из ЭПхеш-образ полученного сообщения открытым ключом отправителя по формуле
 .
.
3. Вычисляется хеш-образ 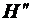 полученного сообщения на стороне получателя по формуле (1).
полученного сообщения на стороне получателя по формуле (1).
4. Сравнивается  и
и 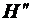 . ЭП признаётся подлинной, если значения хеш-образов совпадают
. ЭП признаётся подлинной, если значения хеш-образов совпадают
 .
.
Например, предположим, что при передаче нашего сообщения «9МАША » оно было изменено на «9МИША ». Проверим подлинность полученного сообщения (рис. 9).
| Хэш-образ из ЭП | 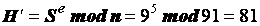
| ||

| Символы принятого сообщения 
| Коды символов 
| Вычисление хеш-образа на стороне получателя

|

| |||
| М | 
| ||
| И | 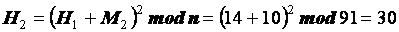
| ||
| Ш | 
| ||
| А | 
| ||
| Вычисленный хэш-образ | 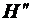 = 29 = 29
|
Рис. 9. Проверка подлинности ЭП
На рис. 9 показано, что ЭП принятого сообщения равна 9, хеш-образ сообщения согласно ЭП  , вычисленный хеш-образ полученного сообщения на стороне получателя открытым ключом отправителя
, вычисленный хеш-образ полученного сообщения на стороне получателя открытым ключом отправителя  . Из неравенства
. Из неравенства  делаем вывод, что при передаче сообщения произошло его случайное или умышленное изменение.
делаем вывод, что при передаче сообщения произошло его случайное или умышленное изменение.
Из рис. 8 и 9 видно, что даже при изменении одной буквы в исходном сообщении, его хеш-образ существенно изменяется. Такие изменения легко выявляются при проверке подлинности электронной подписи.
Задание 10. Создайте хеш-образ сообщения, варианты в табл. 8 приложения, используя число  из 7-го задания, и вычислите его электронную подпись с помощью Вашего закрытого ключа, созданного в задании 7. За хеш-функцию возьмите формулу (1).
из 7-го задания, и вычислите его электронную подпись с помощью Вашего закрытого ключа, созданного в задании 7. За хеш-функцию возьмите формулу (1).
Задание 11. Проверьте подлинность отправленного Вами сообщения и Вашей электронной подписи этого сообщения на стороне получателя, варианты сообщений в табл. 8 приложения.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие прикладные задачи решаются с помощью шифрования?
2. Что такое шифр?
3. Что такое ключ шифра?
4. Что понимается под стойкостью шифра?
5. Что определяет стойкость шифра?
6. К какому классу шифров относится шифр Цезаря?
7. В чём слабость шифра Цезаря?
8. Какая операция используется в шифрах гаммирования?
9. В каких шифрах используется один и тот же ключ для шифрования и дешифрирования?
10. В каких шифрах используются открытые ключи?
11. Кому принадлежит идея шифрования с открытым ключом?
12. На каких математических задачах основаны шифры с открытым ключом?
13. К какому классу шифров относится шифр RSA?
14. Каким ключом зашифровывается RSA-сообщение?
15. Каким ключом дешифрируется RSA-сообщение?
16. Какова длина ключа в RSA-шифре в практических приложениях?
17. Кому принадлежит идея электронной подписи?
18. Какие задачи решает ЭП?
19. Имеет ли смысл ставить ЭП на незашифрованные данные?
20. Что такое хеш-образ сообщения?
21. Сколько ключей используется в механизме ЭП?
22. Каким ключом ставится ЭП на сообщение?
23. Каким ключом проверяется подлинность ЭП?
24. В чём заключается угроза третьего лица в асимметричной криптографии?
25. В чём заключается процедура проверки подлинности ЭП?