Знакоположительные числовые ряды

Определения

 

Ряды в настоящее время представляют собой особо широко используемый математический аппарат для точного и приближенного решения различных уравнений.

Определение 1. Рядом называется сумма некоторой последовательности, другими словами ряд – есть сумма бесконечного числа членов, каждый из которых является элементом заданной последовательности.

 

Ряды бывают двух видов:

1) числовые ряды, если каждый член ряда – число, в этом случае

,

причем в правой части записан числовой ряд, в левой части – его сокращенное обозначение, здесь означает суммирование членов ряда от первого до сколь угодно большого, общий (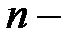 й) член ряда.

2) функциональные ряды, когда каждый член ряда есть функция:

Определение 2. Ряд называется сходящимся, если его сумма имеет конечное значение, если сумма ряда не существует, или равна бесконечности, ряд – расходящийся.

Определение 3. Сумму первых членов ряда называют частичной суммой ряда .

Очевидно, сумма ряда определяется формулой . Однако применение этой формулы сопряжено с большими, порой непреодолимыми, трудностями. Далеко не всегда удается в компактной форме записать ю частичную сумму ряда, а, следовательно, вычислить ее предел. Почленное суммирование ряда - еще менее перспективная процедура, бесконечное число членов не просуммируешь.

Вследствие этого точное значение суммы ряда можно установить в очень небольшом числе случаев.

Приведем пример геометрической прогрессии

,

знаменатель которой .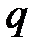

Известна сумма первых 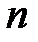членов этого ряда . Вычислим ее предел . Если , то 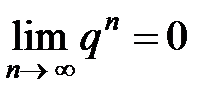, следовательно, . При , и . Ряд расходится. При ряд также расходится. Итак, подтверждается утверждение, что геометрическая прогрессия сходится при и расходится при .

В большинстве случаев приходится вычислять суммы рядов приближенно, но для этого необходимо знать, существует ли конечное значение этой суммы, то есть сходящийся ли ряд.

Теория рядов, следовательно, создана для установления сходимости или расходимости рядов. При необходимости сумму сходящегося ряда вычисляют приближенно, расходящиеся ряды практической ценности не представляют.

 

Числовые ряды

 

Необходимое условие сходимости ряда

 

Если ряд сходится, то .

Доказательство. Если ряд сходящийся, существует его конечная сумма , причем . Вычислим

.

 

Основное свойство рядов

Если ряд сходящийся, то его остаток , образованный отбрасыванием первых членов ряда, тоже сходится. Если ряд расходящийся, то его остаток также является расходящимся рядом.

В самом деле,

.

Если ряд сходится, то существует его конечная сумма , а 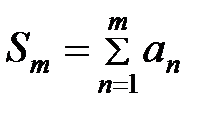- всегда конечна как сумма конечного числа членов. Тогда из следует, что конечное число, и остаток ряда – сходится. Когда ряд расходящийся, . Поскольку сумма ряда в правой части равенства не существует (ряд расходящийся), а имеет конечное значение, сумма ряда в левой части также не существует.

Переходим к рассмотрению частных случаев рядов. Вначале исследуем сходимость числовых рядов.

 

Знакоположительные числовые ряды

Начнем с теорем сравнения знакоположительных рядов.

 

Первая теорема сравнения. Даны два знакоположительных числовых ряда и , причем . Из сходимости большего ряда следует сходимость меньшего ряда. Из расходимости меньшего ряда следует расходимость большего ряда.

 

Доказательство.

1) Пусть ряд сходится, и его сумма 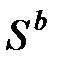конечна. Рассмотрим частичные суммы обоих рядов и . Так как члены обоих рядов положительны, при любо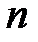м имеем , из условия имеем . Рассмотрим последовательность частичных сумм ряда . Она монотонно возрастает с ростом 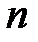(суммируется все большее число положительных членов). В то же время она ограничена сверху числом 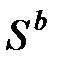. Но имеется теорема, утверждающая, что монотонно возрастающая и ограниченная сверху последовательность имеет конечный предел. Итак, , следовательно, является суммой ряда .

2) Пусть ряд расходится. Поскольку все его члены положительны, его сумма равна бесконечности. По условию теоремы , следовательно, , то есть при неограниченном возрастании суммы неограниченно растет и сумма . Больший ряд также расходится.

 

Вторая теорема сравнения (упрощенная постановка). Даны два знакоположительных ряда и , причем , в этом случае оба ряда ведут себя одинаково: либо оба сходятся, либо оба расходятся.

Доказательство. Из следует, что

.

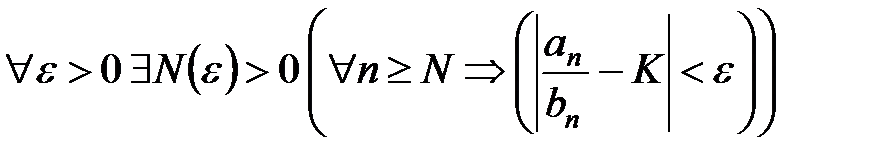Из записанной формулы следует, что начиная с и для всех остальных выполняется неравенство , из которого имеем , или .

1)Рассмотрим правую часть неравенства. Пусть ряд сходится, тогда сходится и его остаток , следовательно, сходится и ряд . Поскольку , из первой части первой теоремы сравнения следует сходимость ряда , а, следовательно, и самого ряда .

2) Пусть ряд расходится, тогда расходится и его остаток 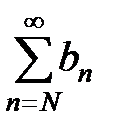. Подберем так, чтобы , тогда ряд тоже расходится. Но из левой части полученного выше неравенства следует, что , значит, члены ряда больше членов расходящегося ряда, из первой теоремы сравнения следует, что ряд расходящийся, расходится и ряд .

Доказано, что из сходимости (расходимости) ряда следует сходимость (расходимость) ряда .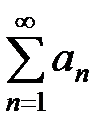

Рассмотрим теперь . Очевидно, , то есть условия только что доказанной теоремы выполнены. Но в этом случае можно утверждать, что из сходимости (расходимости) ряда следует сходимость (расходимость) ряда 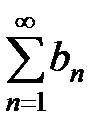. Итак, ряды при выполнении условий теоремы ведут себя одинаково.

 

Доказаны две важнейшие теоремы. Однако для сравнения рядов необходимо иметь информацию о сходимости или расходимости хотя бы нескольких рядов, с которыми можно было бы сравнивать другие ряды.

Для этой цели рассмотрим несколько достаточных условий, позволяющих исследовать сходимость конкретных рядов.

 

Признак Даламбера

сходимости знакоположетельных рядов

 

Теорема. Ряд при условии сходится, когда расходится, если признак Даламбера неприменим.

Доказательство. Если , то

,

откуда следует

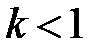1) Для доказательства первой части теоремы воспользуемся правой частью неравенства, записав его в виде , где , . По условию теоремы . Зададим 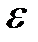настолько малым, чтобы . Тогда

,

,

,

……………………

Рассмотрим теперь два ряда

и

.

Нижний ряд представляет собой сходящуюся геометрическую прогрессию, так как . Члены верхнего ряда меньше соответствующих членов нижнего ряда, на основании первой теоремы сравнения ряд сходится. Но этот ряд является остатком рассматриваемого ряда , следовательно, он тоже сходится.

2) Для доказательства второй части теоремы при воспользуемся полученным ранее неравенством, подобрав так, чтобы . Тогда , то есть положительные члены ряда растут с ростом 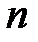. Очевидно, , но ряд может сходиться только в случае . Ряд расходится.

3) При условии невозможно доказать сходимость, или расходимость ряда. Следовательно, в этом случае признак Даламбера неприменим.

 

Рекомендация. Признак Даламбера дает положительный ответ практически всегда, если общий член ряда содержит показательную функцию или факториалы.

Пример 1. . Очевидно, . Тогда

. Ряд сходится.

Пример 2. . .

Чтобы решить этот пример, вспомним некоторые формулы для "факториала" , .

.

Ряд расходится.

 

Радикальный признак Коши

сходимости знакоположительных рядов

Теорема. Дан ряд . Если , а , то ряд сходится, при ряд расходится, при признак не работает.

Доказательство. Из следует, что

,

другими словами, начиная с некоторого и для всех последующих , оттуда следует , или , где , .

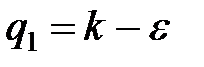1. Докажем справедливость первого утверждения теоремы. В этом случае , зададим так, чтобы выполнялось . Из правой части полученного двойного неравенства следует, что . Если сравнить ряды и , то члены первого ряда меньше соответствующих членов второго ряда, являющегося сходящимся как геометрическая прогрессия со знаменателем меньшим единицы. Из первой теоремы сравнения рядов следует, что ряд , то есть остаток ряда сходится, следовательно, сходится и сам ряд.

2. При доказательстве второго утверждения теоремы учтем, что и зададим так, чтобы . Воспользуемся левой частью двойного неравенства . Сравним ряд с расходящейся геометрической прогрессией 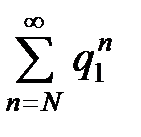. И поскольку члены ряда больше соответствующих членов расходящейся геометрической прогрессии, он расходится. Так как этот ряд является остатком ряда , то и сам ряд расходится.

3. При ряд может как сходиться, так и расходиться, следовательно, признак неприменим.

Замечание. Радикальный признак удобно применять, когда хорошо извлекается корень й степени из общего члена ряда.

Пример 1. . , ряд сходится.

Пример 2. . ,

ряд расходится.

 

 

Интегральный признак Маклорена – Коши

сходимости знакоположительных рядов

Теорема. Знакоположительный ряд сходится (расходится), если сходится (расходится) интеграл , причем подынтегральная функция получается из общего члена ряда заменой дискретно меняющейся переменной 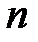на действительную переменную .

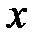Доказательство.

1) Пусть интеграл - сходится, то есть принимает конечное значение. Рассмотрим интеграл , его значение дает площадь криволинейной трапеции, ограниченной прямыми , , и кривой . Разобьем отрезок на равных частей, длина каждого элементарного отрезка равна 1. Из точек разбиения восстановим перпендикуляры до пересечения с кривой, длины этих перпендикуляров , где - члены исследуемого ряда, что следует из условия теоремы. Построим вписанные в криволинейную трапецию прямоугольники, одна из сторон каждого из них равна 1, другие имеют длины соответственно. Подсчитаем сумму площадей вписанных прямоугольников

,

сумма площадей численно равна й частичной сумме ряда без первого члена. Рассмотрим последовательность частичных сумм ряда. Она растет с ростом величины верхнего предела интеграла, так как растет количество вписанных прямоугольников. В то же время любая частичная сумма ряда, как уже говорилось выше, совпадающая численно с площадью вписанных прямоугольников, не может превышать площади криволинейной трапеции, которая сама меньше значения интеграла . Итак, последовательность частичных сумм ряда монотонно возрастает и ограничена сверху, следовательно, она имеет конечный предел , но это сумма ряда по определению. Значит, ряд сходится.

2) Пусть интеграл расходящийся. Так как , то . Построим описанные прямоугольники, одна из сторон каждого из них равна 1, другие соответственно . Сумма площадей этих прямоугольников равна и совпадает с частичной суммой ряда. Поскольку сумма площадей описанных прямоугольников больше площади криволинейной трапеции, которая равна , то и частичные суммы ряда неограниченно возрастают. Очевидно, . Ряд расходится.

Итак, получен универсальный признак сходимости, который, в отличие от предыдущих двух признаков, работает всегда. Но его применение приводит к необходимости исследования сходимости несобственного интеграла, что далеко не просто, да и не всегда возможно.

Исследуем ряд с помощью интегрального признака. Для этого необходимо исследовать сходимость интеграла 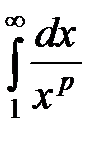, что было проделано ранее. Он сходится при и расходится при . Тогда и ряд сходится при и расходится при .

Пример 1. . Вычислим интеграл

,

 

интеграл сходится и ряд тоже.

Пример 2. . Вычислим интеграл

 

,

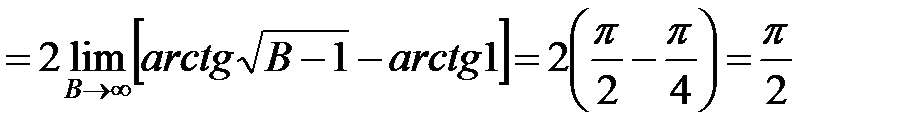интеграл, а вместе с ним ряд сходятся.

 

 

Исследование сходимости знакоположительных рядов с помощью МАКСИМЫ

Рассмотрим ряд

Поскольку не выполняется необходимое условие сходимости ряда (предел n - го члена равен бесконечности), он расходящийся.

Рассмотрим ряд

Поскольку предел n - го члена равен нулю, ряд может как сходиться, так и расходиться. Применение признака Даламбера дает , что меньше 1, ряд сходится.

Исследуем ряд

Проверка необходимого условия показывает, что ряд может и сходиться, и расходиться. Признак Даламбера дает 1, то есть не работает. Интегральный признак приводит к сходящемуся интегралу, следовательно, ряд сходится.

Примеры для самостоятельного решения

 

Исследовать сходимость рядов, используя теоремы сравнения и признаки сходимости

15.1. 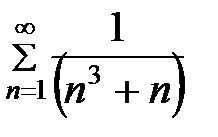, 15.2. , 15.3. , 15.4. ,

15.5. , 15.6. 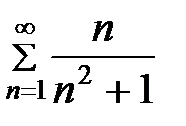, 15.7. , 15.8 ,

15.9. , 15.10. , 15.11. , 15.12. .

 

Ответы. 15.1. Сходится. 15.2. Сходится. 15.3.Сходится. 15.4. Сходится.

15.5. Сходится. 15.6. Расходится. 15.7. Сходится. 15.8. Расходится.

15.9. Сходится. 15.10. Сходится. 15.11. Сходится. 15.12. Расходится.

 

Знакопеременные ряды

 

Альтернативными знакоположительным рядам являются знакопеременные ряды, поскольку исследование знакоотрицательных рядов сводится к знакоположительным рядам вынесением знака (-) за скобки.

Знакопеременные ряды бывают общего вида, когда часть членов ряда положительные, другая часть – отрицательные, и знакочередующиеся, когда знаки членов ряда чередуются, за положительным следует отрицательный член ряда, за отрицательным – положительный.

 

Определение. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов.

Это определение позволяет исследование знакопеременного ряда свести к исследованию знакоположительного ряда.

Не сходящийся абсолютно ряд может сходиться условно, имеется несколько признаков условной сходимости знакопеременных рядов, но они не входят в программу настоящего курса. Ряд, естественно, может расходиться, тогда предел его общего члена при должен быть не равен нулю.

Пример 1. . Это знакопеременный ряд общего вида, первые 9 его членов положительные, 10-й член равен нулю, следующие 9 членов - отрицательные, затем опять нуль, снова 9 положительных членов и т.д. Рассмотрим ряд из модулей и сравним его со сходящимся рядом . Поскольку , из первой теоремы сравнения знакоположительных рядов следует сходимость ряда , а, следовательно, абсолютная сходимость знакопеременного ряда .

Пример 2. . Рассмотрим ряд , он сходится, следовательно, знакочередующийся ряд сходится абсолютно.

Знакочередующиеся ряды

 

Полнее исследованы знакочередующиеся ряды. Здесь не осталось невыясненных вопросов, благодаря теореме Лейбница.

 

Теорема Лейбница условной сходимости знакочередующегося ряда. Дан ряд 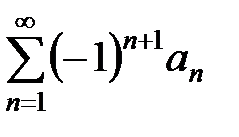, причем . Степень выбрана так, чтобы первый член ряда был положителен, хотя это необязательно.

Если и , ряд сходится условно. Если , ряд расходится.

Доказательство.

1) Рассмотрим частичную сумму ряда, содержащую первых его членов, и представим ее в следующем виде

.

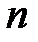Из первого условия теоремы следует, что каждая скобка положительна, следовательно, . При увеличении на единицу к частичной сумме добавляется пара членов, то есть , причем выражение в скобках – положительно. Итак, последовательность четных частичных сумм ряда монотонно возрастает с ростом .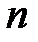

Представим в другом виде

.

 

Поскольку все скобки опять положительны, ясно, что , то есть последовательность четных частичных сумм не только возрастает с ростом 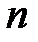, но и ограничена сверху первым членом ряда. В соответствии с известной теоремой, не раз использовавшейся ранее, эта последовательность имеет конечный предел . Однако этого обстоятельства недостаточно, чтобы утверждать, что ряд сходится. В самом деле, все четные частичные суммы ряда равны нулю, ряд не сходится, так как нечетные суммы ряда равны 1. Итак, необходимо рассмотреть нечетные суммы ряда. Очевидно, . Рассмотрим предел нечетных частичных сумм

 

,

поскольку , что следует из второго условия теоремы. Таким образом, последовательности четных и нечетных частичных сумм ряда имеют одинаковый предел, равный , тогда ряд сходится, а его сумма равна .

2) Если 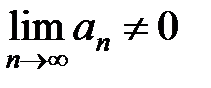, то не выполняется необходимое условие сходимости любого ряда, следовательно, ряд 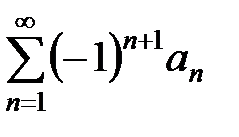расходится. Теорема доказана.

Итак, в отличие от знакоположительных рядов знакочередующиеся ряды могут сходиться абсолютно, условно и расходиться, причем абсолютно сходящийся ряд сходится и условно. Но не наоборот!

Отметим, что от порядка вычисления суммы условно сходящегося ряда (суммирование всех членов подряд, суммирование сначала четных, затем нечетных членов и т.д.) может зависеть значение суммы ряда, то есть сумма условно сходящегося ряда зависит от перестановки членов этого ряда. Поэтому сходимость названа условной. Чтобы получить правильный ответ, необходимо суммировать члены ряда подряд, один за другим.

 

Примеры.

1. . Ряд из модулей сходится , следовательно, рассматриваемый знакочередующийся ряд сходится абсолютно.

 

 

2. . Рассмотрим ряд из абсолютных величин членов .

Он расходится . Следовательно, исследуемый ряд не сходится абсолютно. Поскольку , ряд сходится условно.

3. . Поскольку , не выполняется и условие теоремы Лейбница, и необходимое условие сходимости ряда. Ряд расходящийся.

 

Исследование знакочередующегося ряда с помощью МАКСИМЫ

 

Исследуем ряд

Ряд из модулей знакочередующегося ряда сходится на основании интегрального признака (признак Даламбера не работает), следовательно, исследуемый ряд сходится абсолютно.

Рассмотрим ряд

Исследуемый ряд не сходится абсолютно, при этом признак Даламбера не работает, интегральный признак приводит к расходящемуся интегралу. И поскольку предел n – го члена равен 0, на основании теоремы Лейбница ряд сходится условно.

Примеры для самостоятельного решения

 

Исследовать сходимость знакочередующихся рядов

15.13. , 15.14. , 15.15. , 15.16. .

 

Ответы. 15.13. Сходится абсолютно, 15.14. Сходится условно, 15.15. Расходится, 15.16. Сходится абсолютно.

Функциональные ряды

 

Если числовые ряды в настоящее время используются, в основном для отработки методики исследования их сходимости, то функциональные ряды имеют широчайшее применение при решении различных уравнений, особенно в случаях, когда их точное решение построить не удается. Более того, решение уравнения в виде ряда считается точным, если сходимость ряда доказана. Не менее успешно используются функциональные ряды при вычислении приближенных значений некоторых функций. Точное значение даже такой простой функции, как , известно только для нескольких значений аргумента ( и так далее). Чтобы подсчитать значение этой функции в промежуточных точках, используется представление в виде ряда. Кстати, при вычислении этой функции с помощью компьютера или микрокалькулятора фактически используется ее "разложение в ряд".

Широкую известность получили степенные ряды, ряд Фурье и различные его модификации.