Рассмотрим сходимость и равномерную сходимость остатка ряда 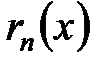 , что несколько проще, но приводит к тому же результату. Используем для этого теорию числовых рядов. Пусть
, что несколько проще, но приводит к тому же результату. Используем для этого теорию числовых рядов. Пусть 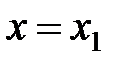 , тогда
, тогда  есть числовой ряд. Он может сходиться или расходиться. Пусть этот ряд сходящийся, тогда
есть числовой ряд. Он может сходиться или расходиться. Пусть этот ряд сходящийся, тогда
 .
.
Пусть при 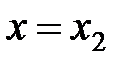 числовой ряд
числовой ряд  также сходится, тогда
также сходится, тогда
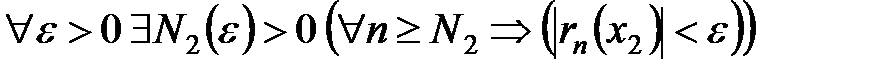 .
.
Нетрудно понять, что один из этих рядов может сходиться медленнее, чем другой, следовательно, 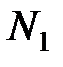 и
и  не обязательно равны, то есть
не обязательно равны, то есть  .
.
В результате, если остаток ряда сходится в некоторой области, то
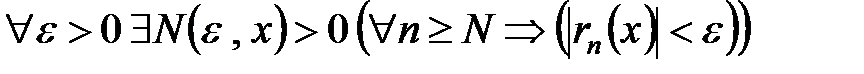 ,
,
отсюда следует, что при сходимости ряда в некоторой области для всех 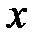 из этой области выполняется условие
из этой области выполняется условие
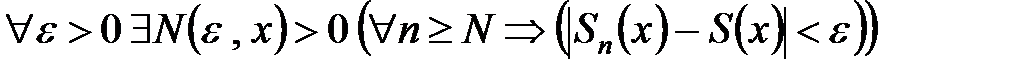
Для некоторых рядов удается определить область, где выполняется условие
 ,
,
то есть значение 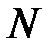 одинаково для всех точек рассматриваемой области. В этом случае ряд называется равномерно сходящимся в этой области.
одинаково для всех точек рассматриваемой области. В этом случае ряд называется равномерно сходящимся в этой области.
Покажем на примере, что некоторые ряды являются равномерно сходящимися, но есть и такие сходящиеся ряды, которые не сходятся равномерно.
Пример 1. Рассмотрим ряд
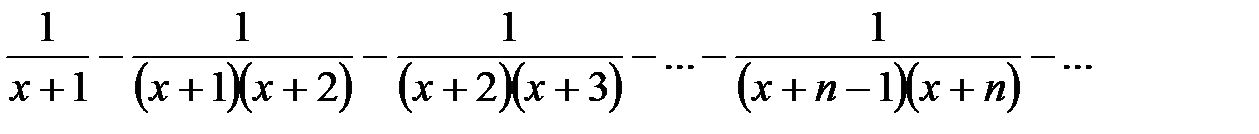
в области 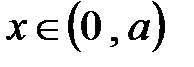 , где
, где 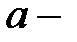 любое положительное число.
любое положительное число.
Легко установить, что данный ряд можно представить в виде
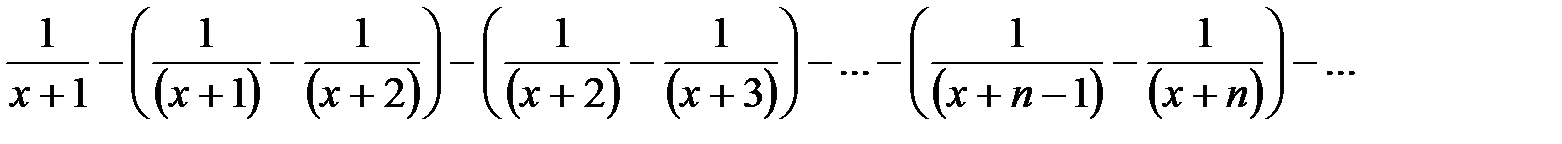
Подсчитаем  ю частичную сумму ряда, предварительно раскрыв скобки, очевидно,
ю частичную сумму ряда, предварительно раскрыв скобки, очевидно,  . Определим сумму ряда
. Определим сумму ряда 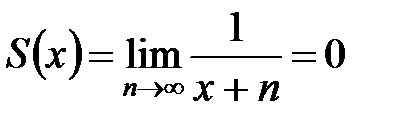 . Поскольку
. Поскольку 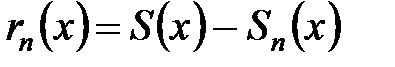 , имеем
, имеем 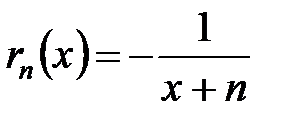 , а
, а 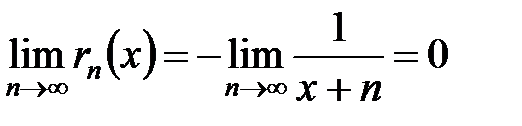 .
.
Но в этом случае
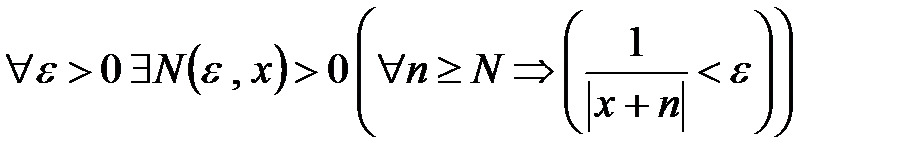 ,
,
откуда следует, что 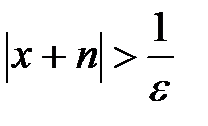 и, поскольку
и, поскольку  и
и 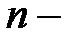 положительные числа, то
положительные числа, то
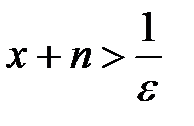 , откуда имеем
, откуда имеем 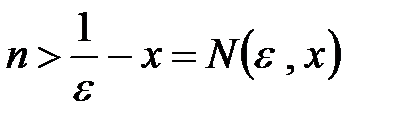 . Итак, установлено
. Итак, установлено 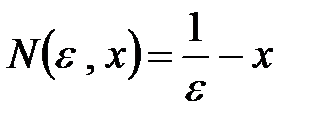 , начиная с которого выполняется условие сходимости остатка ряда. Следовательно, ряд в области
, начиная с которого выполняется условие сходимости остатка ряда. Следовательно, ряд в области 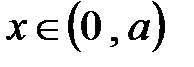 сходится.
сходится.
Если мы выберем 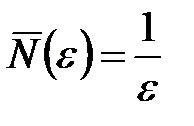 , то
, то 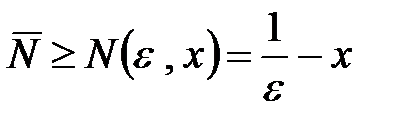 при любых
при любых 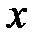 из заданной области, следовательно, условие
из заданной области, следовательно, условие
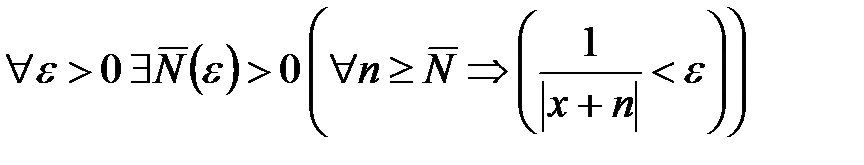
выполняется при любом  , и
, и 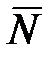 не зависит от
не зависит от 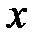 . Ряд в указанной области сходится равномерно.
. Ряд в указанной области сходится равномерно.
Пример 2. Рассмотрим ряд
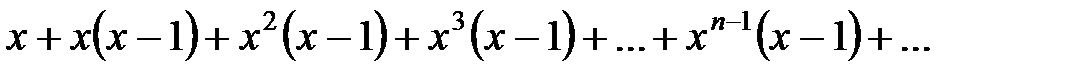
в области 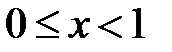 . Запишем
. Запишем  , предварительно раскрыв скобки и произведя сокращения. Тогда
, предварительно раскрыв скобки и произведя сокращения. Тогда 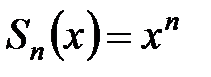 . Сумма ряда в указанной области
. Сумма ряда в указанной области  . Остаток ряда
. Остаток ряда 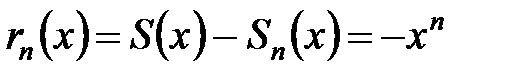 , причем
, причем  . Определим
. Определим 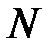 , начиная с которого выполняется условие
, начиная с которого выполняется условие  . Очевидно, в заданной области из
. Очевидно, в заданной области из 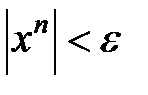 следует
следует 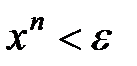 . Логарифмируя, получаем
. Логарифмируя, получаем 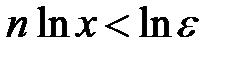 . Поскольку в рассматриваемой области
. Поскольку в рассматриваемой области 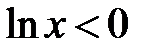 ,
, 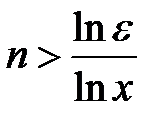 . Итак,
. Итак,  . При этом невозможно найти такое
. При этом невозможно найти такое 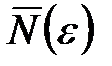 , не зависящее
, не зависящее 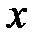 , чтобы выполнялось условие равномерной сходимости. Дело в том, что при
, чтобы выполнялось условие равномерной сходимости. Дело в том, что при 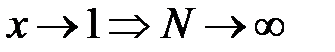 , то есть с ростом
, то есть с ростом 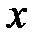 число
число 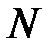 растет до сколь угодно больших величин. Отметим, что при
растет до сколь угодно больших величин. Отметим, что при 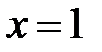 не равным нулю остается только первый член. Итак, в области
не равным нулю остается только первый член. Итак, в области 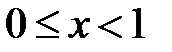 ряд сходится, но не равномерно.
ряд сходится, но не равномерно.
Свойства равномерно сходящихся рядов
1. Если члены ряда 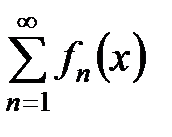 - есть непрерывные в некоторой области
- есть непрерывные в некоторой области 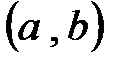 функции, а ряд в этой области сходится равномерно, то сумма ряда - непрерывная в этой области функция.
функции, а ряд в этой области сходится равномерно, то сумма ряда - непрерывная в этой области функция.
2. Если члены ряда непрерывные в области 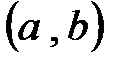 функции и ряд сходится в ней равномерно, то его можно почленно интегрировать в любых пределах, лежащих в указанном промежутке, причем
функции и ряд сходится в ней равномерно, то его можно почленно интегрировать в любых пределах, лежащих в указанном промежутке, причем
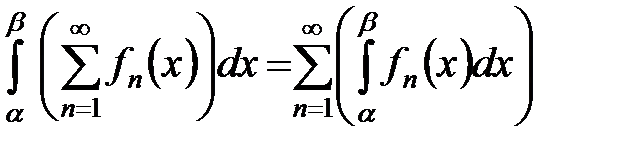 .
.
3. Если ряд 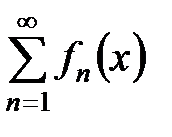 сходится в промежутке
сходится в промежутке 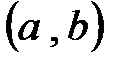 , и его члены имеют непрерывные в этом промежутке производные
, и его члены имеют непрерывные в этом промежутке производные 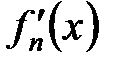 , причем ряд из производных
, причем ряд из производных  сходится в
сходится в 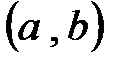 равномерно, то ряд
равномерно, то ряд 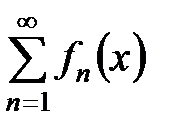 также сходится равномерно, и его можно дифференцировать почленно, причем
также сходится равномерно, и его можно дифференцировать почленно, причем
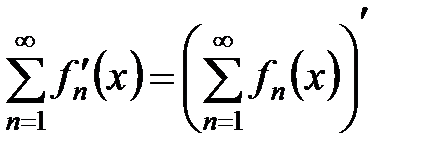 .
.
Степенные ряды
Ряд 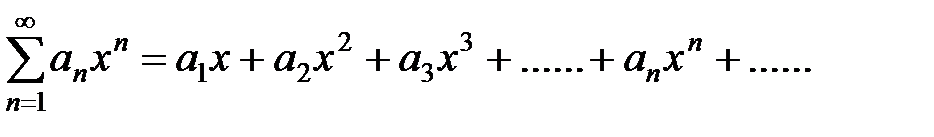 , где
, где 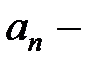 постоянные коэффициенты, называется степенным. Очевидно, этот ряд есть частный случай функционального ряда, следовательно, не обязательно сходится при любых
постоянные коэффициенты, называется степенным. Очевидно, этот ряд есть частный случай функционального ряда, следовательно, не обязательно сходится при любых  . Естественно, представляет интерес определение области сходимости степенного ряда, то есть то множество значений аргумента
. Естественно, представляет интерес определение области сходимости степенного ряда, то есть то множество значений аргумента 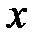 , при которых ряд сходится.
, при которых ряд сходится.
Теорема. Степенной ряд 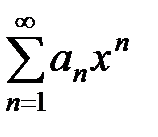 сходится абсолютно в области
сходится абсолютно в области 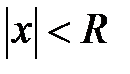 , где
, где 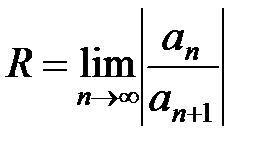 , и расходится в области
, и расходится в области 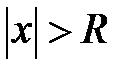 .
.
Доказательство. Поскольку  , да и
, да и  не обязательно положительны, ряд, вообще говоря, является знакопеременным. Чтобы доказать абсолютную сходимость ряда, необходимо рассмотреть ряд из абсолютных величин членов этого ряда
не обязательно положительны, ряд, вообще говоря, является знакопеременным. Чтобы доказать абсолютную сходимость ряда, необходимо рассмотреть ряд из абсолютных величин членов этого ряда 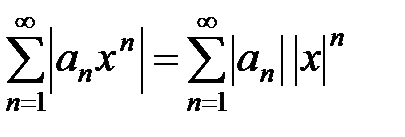 . Теперь к знакоположительному числовому ряду применим признак Даламбера:
. Теперь к знакоположительному числовому ряду применим признак Даламбера: 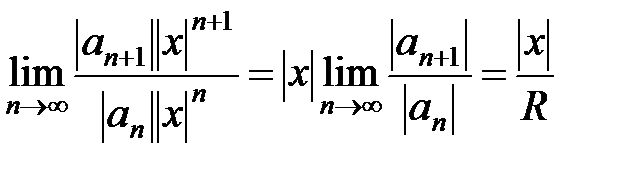 , где
, где 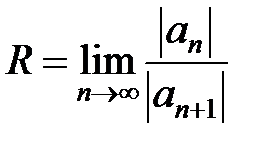 . В соответствии с признаком Даламбера рассматриваемый ряд сходится при
. В соответствии с признаком Даламбера рассматриваемый ряд сходится при 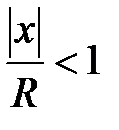 и расходится в области
и расходится в области  . Итак, область абсолютной сходимости степенного ряда
. Итак, область абсолютной сходимости степенного ряда 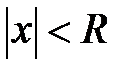 , где
, где  . В области
. В области 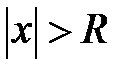 ряд расходится.
ряд расходится.
Вследствие этого, промежуток 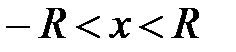 называется областью абсолютной сходимости степенного ряда, а
называется областью абсолютной сходимости степенного ряда, а  называют радиусом его сходимости.
называют радиусом его сходимости.
Замечания.
1). Признак Даламбера не работает, если предел равен единице, следовательно, он неприменим при 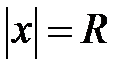 (
(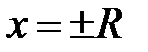 ). Исследование сходимости рядов в этих точках производится отдельно.
). Исследование сходимости рядов в этих точках производится отдельно.
2). При выведении формулы радиуса сходимости степенной ряд считался "полным", то есть в нем присутствовали все целые, положительные степени  . Если ряд не содержит всех степеней
. Если ряд не содержит всех степеней  , формула для радиуса сходимости будет неверной. В этом случае при исследовании сходимости каждого конкретного степенного ряда следует составить ряд из модулей его членов, после чего применить признак Даламбера. Очевидно, такую процедуру можно применять и при определении области сходимости и "полных" рядов.
, формула для радиуса сходимости будет неверной. В этом случае при исследовании сходимости каждого конкретного степенного ряда следует составить ряд из модулей его членов, после чего применить признак Даламбера. Очевидно, такую процедуру можно применять и при определении области сходимости и "полных" рядов.
Пример 1.
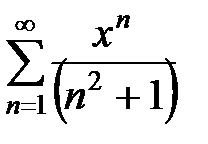 . Ряд "полный", его можно исследовать двумя способами.
. Ряд "полный", его можно исследовать двумя способами.
Первый способ.
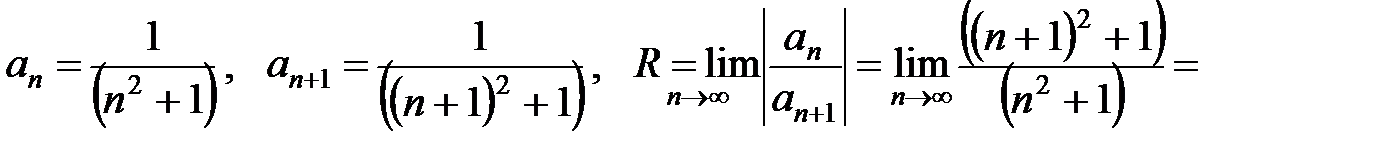
 .
.
Итак, 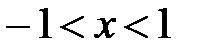 .
.
Второй способ. Рассматривается ряд 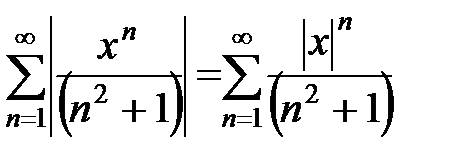 . Пусть
. Пусть 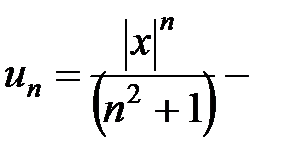 общий член этого ряда, тогда
общий член этого ряда, тогда 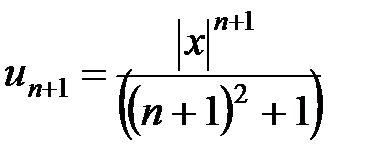 . Применяем признак Даламбера
. Применяем признак Даламбера
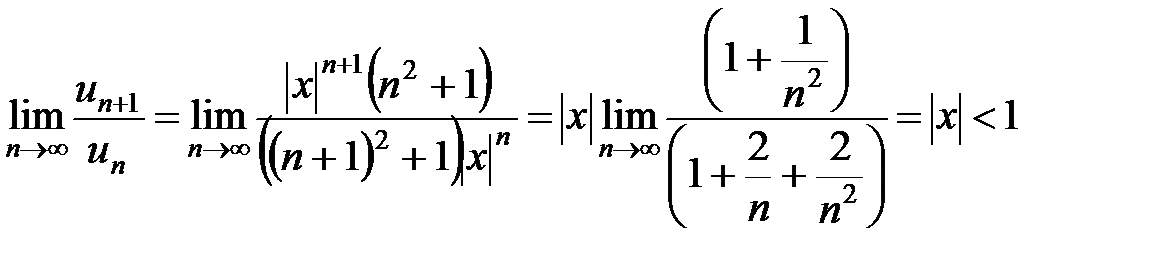 .
.
Естественно, получается тот же результат.
Исследуем граничные значения области сходимости.
При 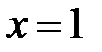 получаем числовой ряд
получаем числовой ряд  . Ряд знакоположительный, его члены меньше членов сходящегося ряда
. Ряд знакоположительный, его члены меньше членов сходящегося ряда  , следовательно, он сходится.
, следовательно, он сходится.
При 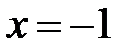 имеем знакочередующийся числовой ряд
имеем знакочередующийся числовой ряд 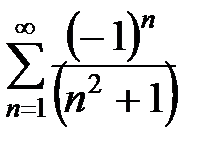 . Рассмотрим ряд из модулей его членов
. Рассмотрим ряд из модулей его членов 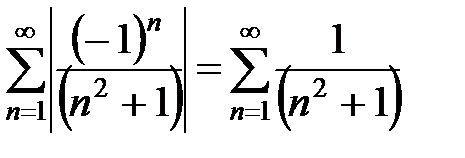 , но это сходящийся ряд, что мы только что подтвердили, следовательно, знакочередующийся ряд сходится абсолютно. Итак, область абсолютной сходимости исследуемого ряда
, но это сходящийся ряд, что мы только что подтвердили, следовательно, знакочередующийся ряд сходится абсолютно. Итак, область абсолютной сходимости исследуемого ряда 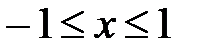 . При остальных значениях
. При остальных значениях  ряд расходится.
ряд расходится.
Пример 2. Ряд 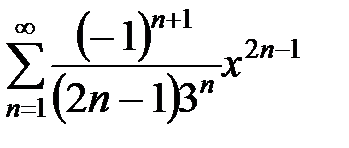 "неполный", так как содержит только нечетные степени
"неполный", так как содержит только нечетные степени  . Применяем второй способ, рассмотрев ряд из абсолютных величин членов исходного ряда
. Применяем второй способ, рассмотрев ряд из абсолютных величин членов исходного ряда  . Применим к нему признак Даламбера. Общий член ряда
. Применим к нему признак Даламбера. Общий член ряда 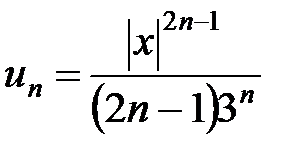 , тогда
, тогда  . Подсчитаем предел
. Подсчитаем предел
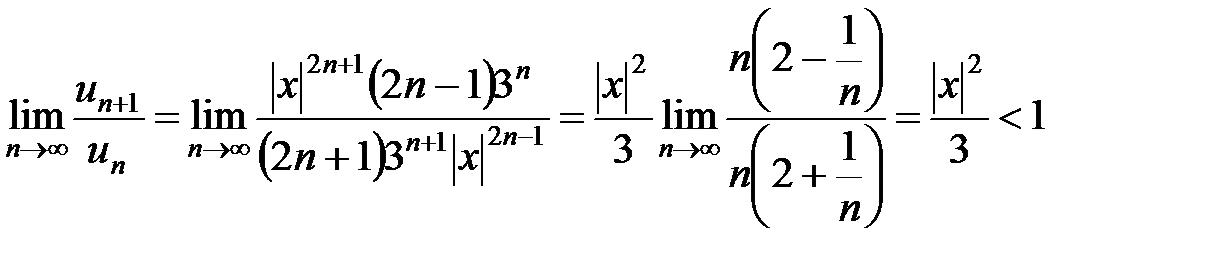 .
.
Получаем область сходимости 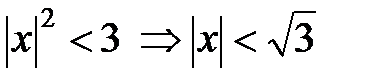 или
или 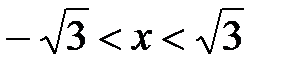 .
.
Исследуем граничные точки:
при 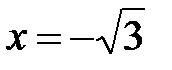 имеем
имеем 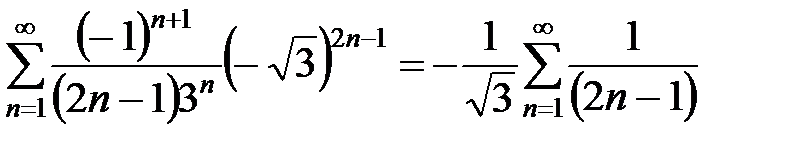 . Знакоположительный ряд
. Знакоположительный ряд 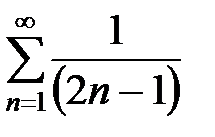 расходится, что следует из сравнения его с расходящимся рядом
расходится, что следует из сравнения его с расходящимся рядом 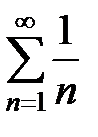 с помощью второй теоремы сравнения. Предел отношения членов этих рядов
с помощью второй теоремы сравнения. Предел отношения членов этих рядов  . Поскольку значение предела больше нуля и меньше бесконечности, ряды ведут себя одинаково. Очевидно, расходится и получившийся на границе знакоотрицательный ряд;
. Поскольку значение предела больше нуля и меньше бесконечности, ряды ведут себя одинаково. Очевидно, расходится и получившийся на границе знакоотрицательный ряд;
при 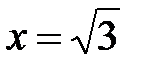 имеем
имеем 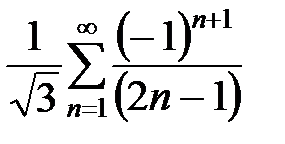 . Это знакочередующийся ряд, он сходится условно, так как
. Это знакочередующийся ряд, он сходится условно, так как 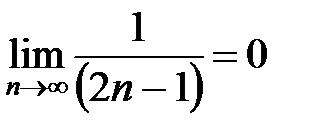 .
.
Итак, область сходимости ряда 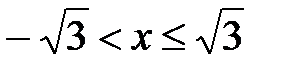 .
.
Свойства степенных рядов
1. Сумма степенного ряда в области (промежутке) его сходимости есть непрерывная функция.
2. Степенной ряд в его области (промежутке) сходимости можно почленно интегрировать, причем сумма нового ряда равна интегралу от суммы исходного ряда.
3. Степенной ряд в промежутке его сходимости можно почленно дифференцировать, сумма продифференцированного ряда равна производной суммы исходного ряда.
Примечание. Часто встречаются степенные ряды, более общего вида
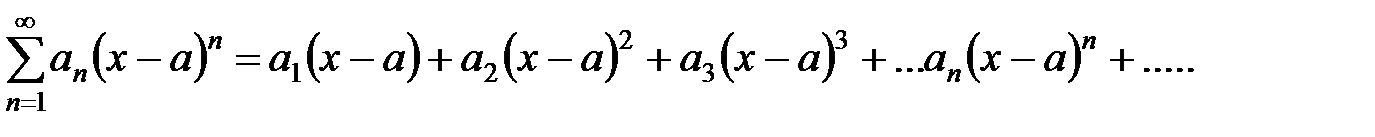 .
.
При исследовании их области сходимости делается замена  , приводящая ряд к уже известному ряду
, приводящая ряд к уже известному ряду 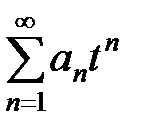 .
.
Исследование степенных рядов с помощью МАКСИМЫ
Рассмотрим изученный выше ряд 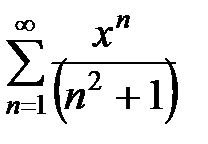

Итак, радиус сходимости 1. В граничных точках области ряды сходятся в соответствии с третьей командой. Область сходимости ряда 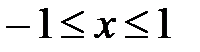 .
.
Примеры для самостоятельного решения
Исследовать сходимость степенных рядов
16.1.  , 16.2.
, 16.2. 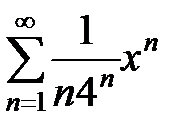 , 16.3.
, 16.3. 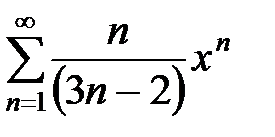 , 16.4.
, 16.4.  ,
,
16.5. 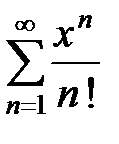 , 16.6.
, 16.6. 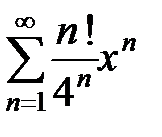 , 16.7.
, 16.7.  , 16.8.
, 16.8. 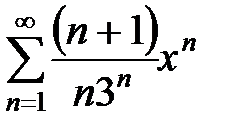 .
.
Ответы.
16.1. 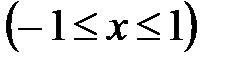 , 16.2.
, 16.2.  , 16.3.
, 16.3. 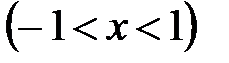 , 16.4.
, 16.4.  ,
,
16.5.  , 16.6.
, 16.6. 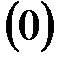 , 16.7.
, 16.7. 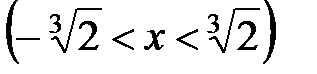 , 16.8.
, 16.8. 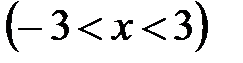 .
.
Ряд Тейлора
В первой части курса для 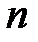 раз дифференцируемой функции была получена формула Тейлора
раз дифференцируемой функции была получена формула Тейлора
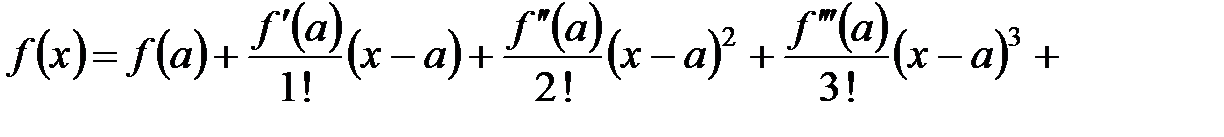
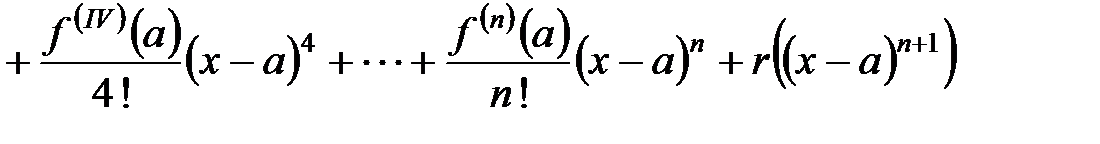 ,
,
и ее частный случай – формула Маклорена
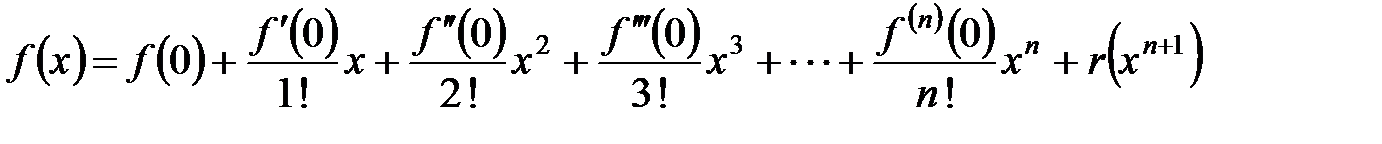 .
.
Вопрос ставится так, нельзя ли обобщить формулу Тейлора для бесконечно дифференцируемой функции, представив ее в виде ряда.
Поскольку формула Тейлора превращается в формулу Маклорена при помощи замены  , не нарушая общности рассуждений, рассмотрим такую возможность для формулы Маклорена.
, не нарушая общности рассуждений, рассмотрим такую возможность для формулы Маклорена.
Пусть
 ,
,
тогда 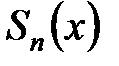 - основная часть формулы Маклорена - является одновременно частичной суммой степенного ряда
- основная часть формулы Маклорена - является одновременно частичной суммой степенного ряда 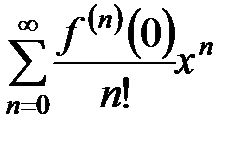 . В соответствии с формулой Маклорена
. В соответствии с формулой Маклорена
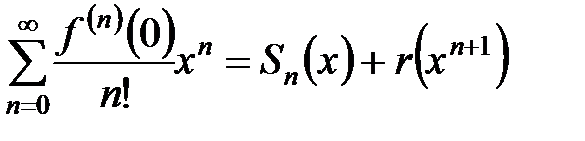 ,
,
то есть остаток в формуле Маклорена 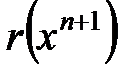 должен являться остатком степенного ряда. Но предел остатка ряда при
должен являться остатком степенного ряда. Но предел остатка ряда при 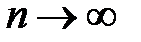 должен стремиться к нулю, что следует из теории рядов. Таким образом, представление
должен стремиться к нулю, что следует из теории рядов. Таким образом, представление 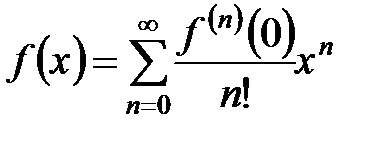 возможно при выполнении условия
возможно при выполнении условия 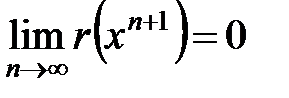 и, конечно, в области сходимости степенного ряда.
и, конечно, в области сходимости степенного ряда.
Имеются различные формы представления остатка в формуле Маклорена. Представим остаток в форме Лагранжа 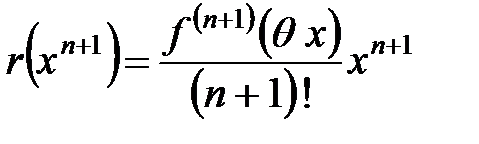 ,
,
где 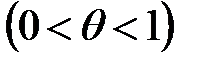 . Проведем его оценку абсолютной величины остатка
. Проведем его оценку абсолютной величины остатка 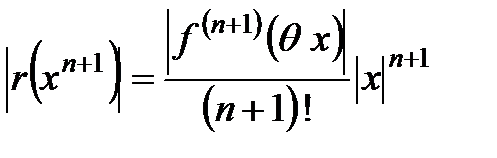 , для чего с помощью признака Даламбера исследуем сходимость ряда
, для чего с помощью признака Даламбера исследуем сходимость ряда  :
:  при любом конечном значении
при любом конечном значении 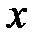 . Но для сходящегося ряда должно выполняться необходимое условие сходимости
. Но для сходящегося ряда должно выполняться необходимое условие сходимости 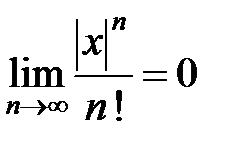 , то есть при
, то есть при  и любом конечном значении
и любом конечном значении 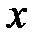 как
как  , так и
, так и  стремятся к нулю. Значит, при
стремятся к нулю. Значит, при 
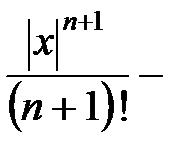 бесконечно малая функция. Если функция
бесконечно малая функция. Если функция 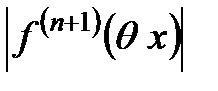 - ограничена, то
- ограничена, то 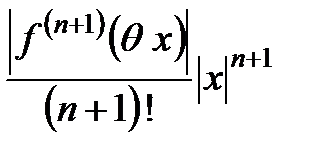 также бесконечно малая, следовательно,
также бесконечно малая, следовательно,
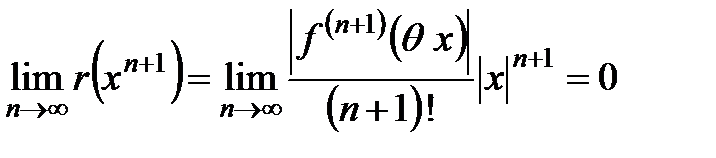 .
.
Разложение в ряд функции 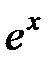
В первой части курса математического анализа была получена формула Маклорена для этой функции. Приведем эту формулу, приняв остаточный член в форме Лагранжа
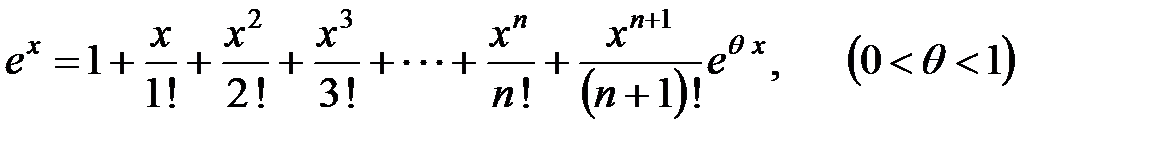 ,
,
Рассмотрим остаток ряда  . Как уже говорилось выше, первый сомножитель в этом выражении при
. Как уже говорилось выше, первый сомножитель в этом выражении при  и любом конечном значении
и любом конечном значении 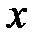 – есть бесконечно малая функция. Но
– есть бесконечно малая функция. Но 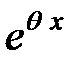 также при любом значении
также при любом значении 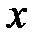 - ограниченная величина:
- ограниченная величина: 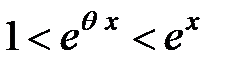 . Известно, что бесконечно малая, умноженная на ограниченную функцию, также является бесконечно малой и
. Известно, что бесконечно малая, умноженная на ограниченную функцию, также является бесконечно малой и 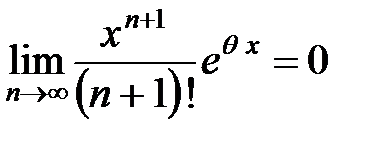 , следовательно,
, следовательно, 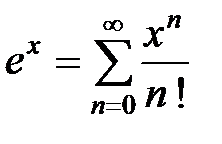 , конечно, в области сходимости ряда. Определим радиус сходимости ряда
, конечно, в области сходимости ряда. Определим радиус сходимости ряда  . Поскольку
. Поскольку 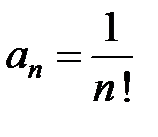 ,
, 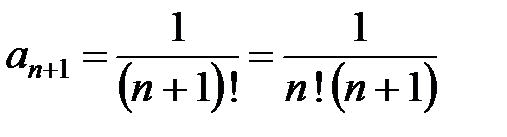 . Тогда
. Тогда  . Область сходимости ряда для функции
. Область сходимости ряда для функции 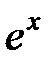 , следовательно,
, следовательно, 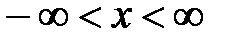 .
.
Эта область фактически уже определена выше с помощью признака Даламбера, в результате применения которого установлено, что предел при любом 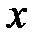 равен нулю, и ряд сходится абсолютно при любом
равен нулю, и ряд сходится абсолютно при любом  .
.
Разложение с помощью МАКСИМЫ
D формуле Тейлора 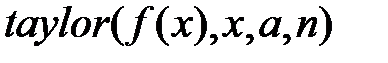 первым параметром является разлагаемая функция, второй указывает, по какой переменной происходит разложение, третий – в окрестности какой точки это разложение (в ряде Маклорена
первым параметром является разлагаемая функция, второй указывает, по какой переменной происходит разложение, третий – в окрестности какой точки это разложение (в ряде Маклорена 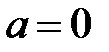 ), последний аргумент задает количество членов разложениия
), последний аргумент задает количество членов разложениия
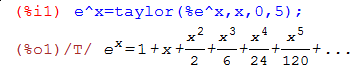
Представление в виде рядов функций 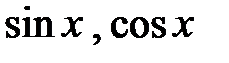 .
.
Запишем формулы Маклорена для функций 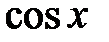 и
и 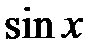 . И представим остаточные члены в форме Лагранжа. Пусть
. И представим остаточные члены в форме Лагранжа. Пусть 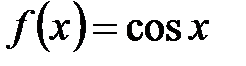 . Тогда
. Тогда
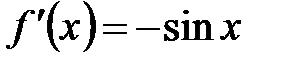 ,
, 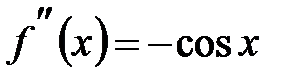 ,
, 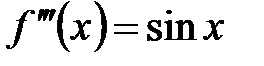 ,
, 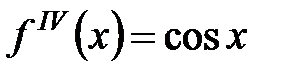 .
.
Покажем, что 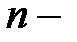 я производная вычисляется по формуле
я производная вычисляется по формуле  . В самом деле, при
. В самом деле, при  имеем
имеем 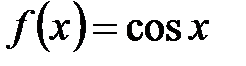 , при
, при 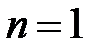 получаем
получаем 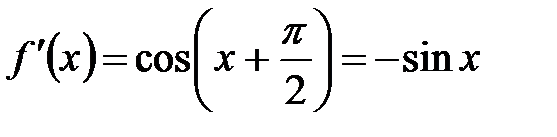 , при
, при 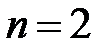 , очевидно,
, очевидно,  , при
, при 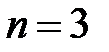 имеем
имеем 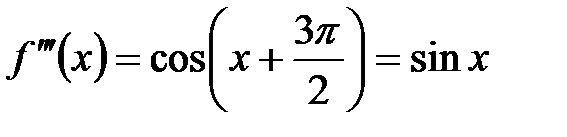 ,
,
при 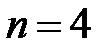
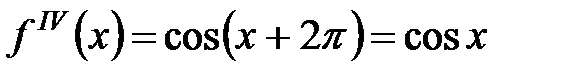 и так далее. Нетрудно заметить, что формула для
и так далее. Нетрудно заметить, что формула для  ой производной верна. Отсюда следует, что при
ой производной верна. Отсюда следует, что при 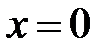 функция равна 1, все ее нечетные производные равны нулю, а четные равны
функция равна 1, все ее нечетные производные равны нулю, а четные равны 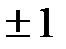 . Формула Маклорена принимает вид
. Формула Маклорена принимает вид
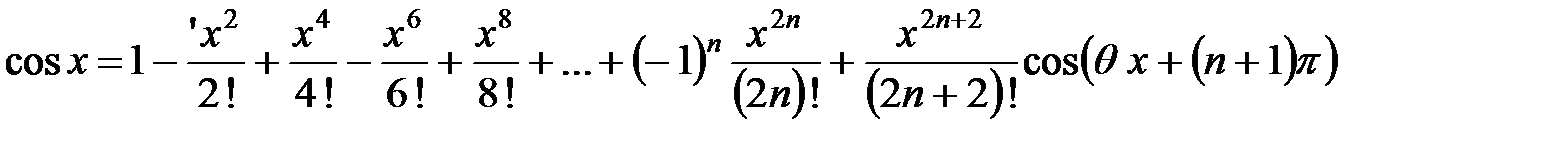 ,
,
( ).
).
Докажем, что 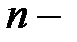 я производная функции
я производная функции  может быть представлена формулой
может быть представлена формулой 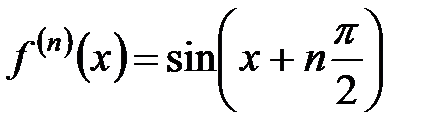 .
.
Проверим это. 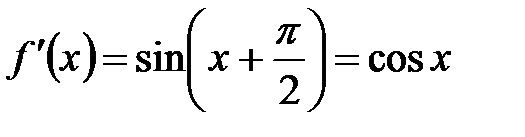 ,
,  ,
, 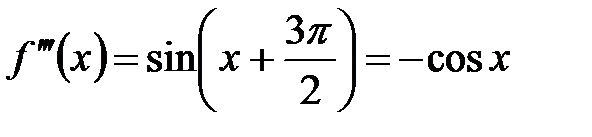 ,
, 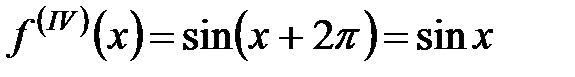 и так далее.
и так далее.
Из формулы для 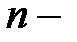 ой производной имеем при
ой производной имеем при  функция
функция 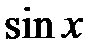 и ее четные производные равны нулю, а нечетные
и ее четные производные равны нулю, а нечетные 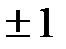 . Итак,
. Итак,
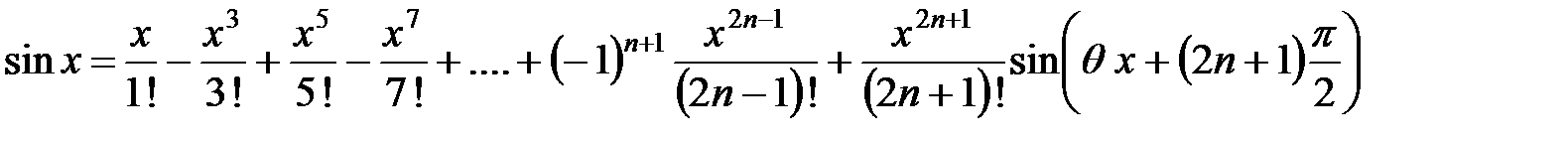 .
.
Поскольку
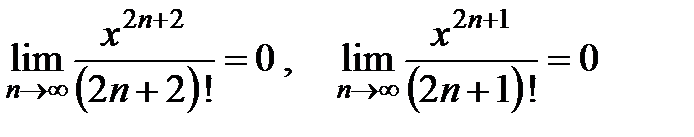 ,
, 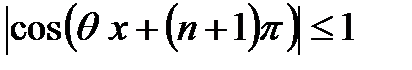 ,
, 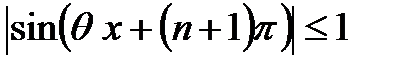 ,
,
имеем
 ,
, 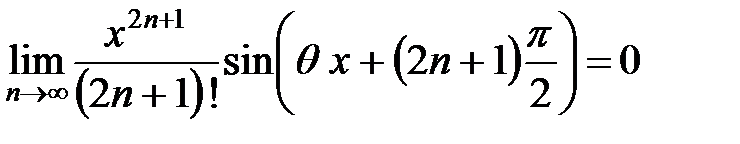 .
.
Таким образом,
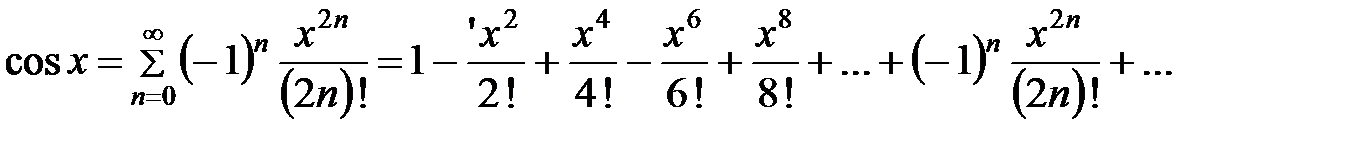 ,
,
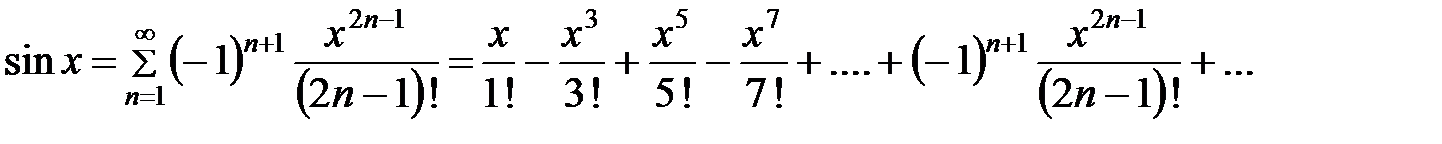 ..
..
Поскольку остаточные члены обоих рядов стремятся к нулю при  , областью сходимости обоих рядов является вся числовая ось.
, областью сходимости обоих рядов является вся числовая ось.
Проверим этот результат, для чего исследуем ряды из абсолютных величин
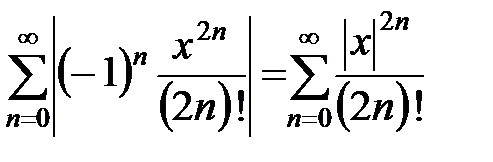 ,
, 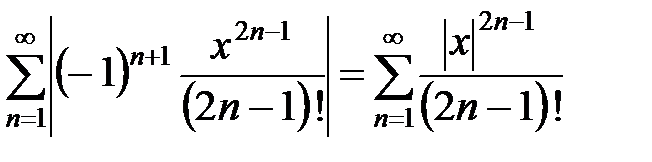 .
.
В соответствии с признаком Даламбера
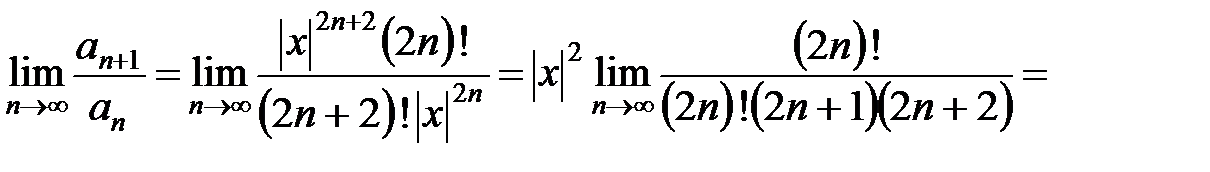
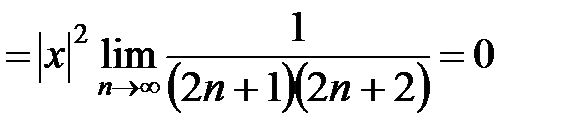 ,
,

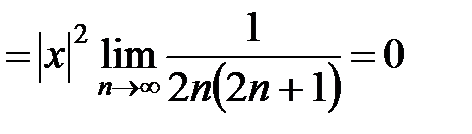
пределы в обоих случаях равны 0 при любых  , и в соответствии с признаком Даламбера область сходимости рядов для
, и в соответствии с признаком Даламбера область сходимости рядов для 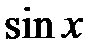 и
и 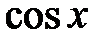 , действительно,
, действительно,  .
.
Разложение в МАКСИМЕ

Разложение в ряд функции 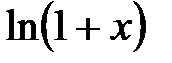
Используем геометрическую прогрессию, рассмотренную в начале темы "Ряды"
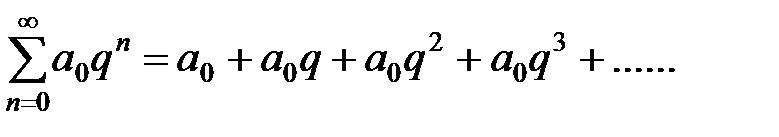 ,
,
Она сходится, если 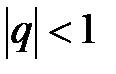 . При
. При 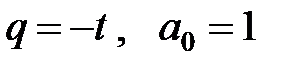 геометрическая прогрессия представляет собой степенной ряд
геометрическая прогрессия представляет собой степенной ряд
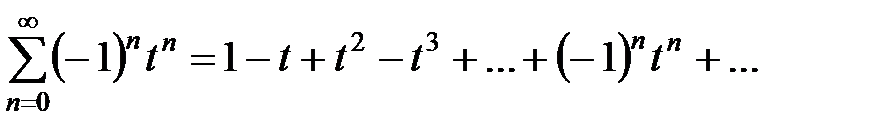 ,
,
сходящийся, естественно, в области 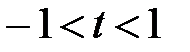 . Его сумма была определена выше, она равна
. Его сумма была определена выше, она равна 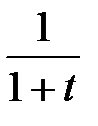 .
.
Как уже говорилось, степенной ряд можно почленно интегрировать в промежутке его сходимости. Выберем некоторое  и вычислим
и вычислим
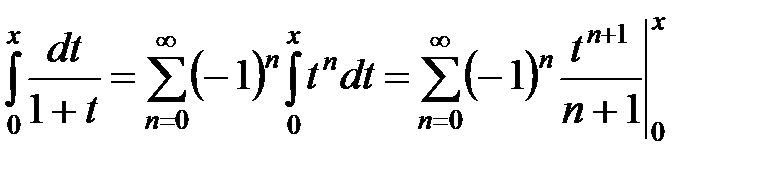 ,
,
откуда следует
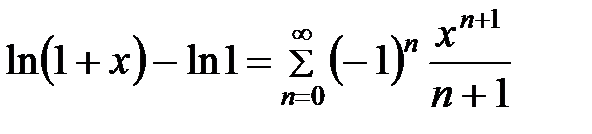 ,
,
или
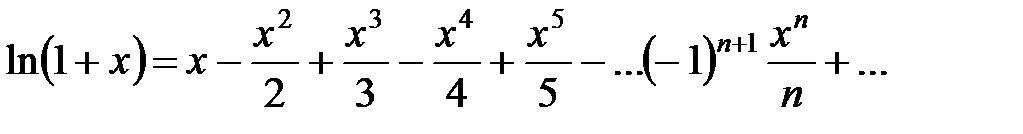 .
.
Ряд сходится в той же области  , что легко проверяется.
, что легко проверяется.
В МАКСИМЕ

Формула Эйлера
При рассмотрении комплексных чисел использовалась без доказательства формула Эйлера 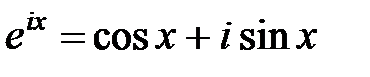 . Теперь появилась возможность ее доказать. Используем разложение функции
. Теперь появилась возможность ее доказать. Используем разложение функции
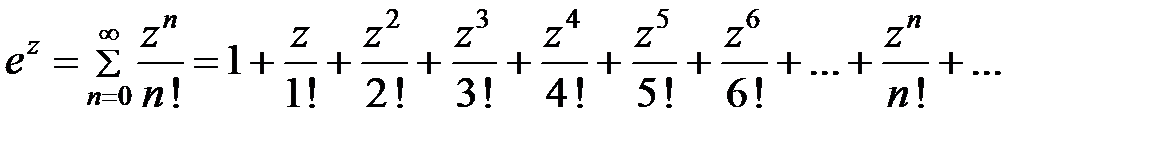 .
.
Примем 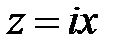 (в разложении использована договоренность, что
(в разложении использована договоренность, что 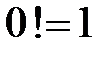 ). Тогда
). Тогда
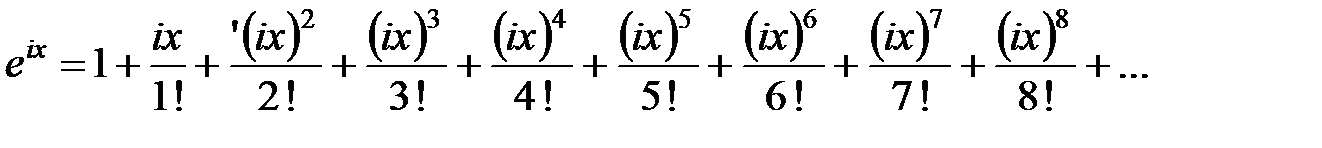 .
.
Если учесть, что 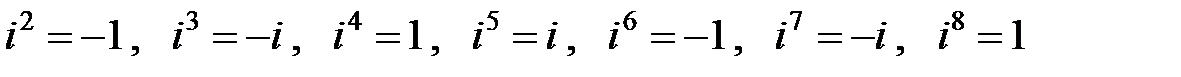 и т.д., то
и т.д., то
 ,
,
Сравнивая полученное выражение с разложениями
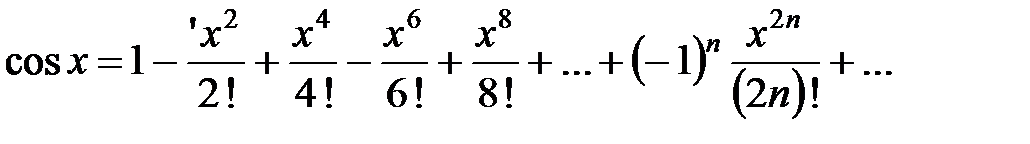 ,
,
 ,
,
нетрудно убедиться, что формула Эйлера справедлива.
Ряды Фурье
Наряду со степенными рядами к наиболее распространенным функциональным рядам относятся ряды Фурье.
Классический ряд Фурье – это ряд вида
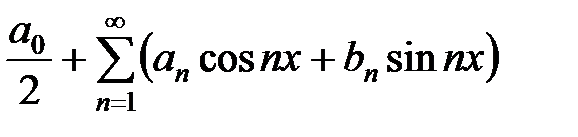 ,
,
где  постоянные коэффициенты. Таким образом, ряды Фурье - тригонометрические, а их сумма - периодическая функция с периодом
постоянные коэффициенты. Таким образом, ряды Фурье - тригонометрические, а их сумма - периодическая функция с периодом 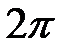 .
.
Данное обстоятельство существенно ограничивает область применимости рядов Фурье, так как далеко не всякий реально происходящий процесс является периодическим, да еще с периодом 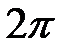 . Поэтому основные усилия математиков были направлены на смягчение указанных ограничений путем внесения некоторых дополнительных условий, о чем будет сказано ниже.
. Поэтому основные усилия математиков были направлены на смягчение указанных ограничений путем внесения некоторых дополнительных условий, о чем будет сказано ниже.
Рассмотрим систему функций, входящих в ряд Фурье

Эта система функций обладает двумя важнейшими свойствами - ортогональностью и полнотой.
Определение 1. Систему функций 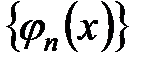 называют ортогональной на некотором промежутке
называют ортогональной на некотором промежутке 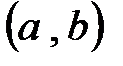 , если выполняются условия:
, если выполняются условия:
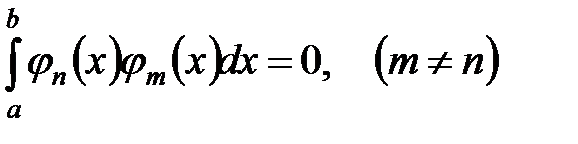 ,
, 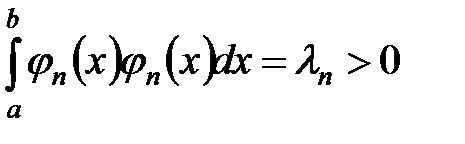 .
.
Когда  , система называется нормальной.
, система называется нормальной.
Покажем, что система функций

является ортогональной системой на интервале 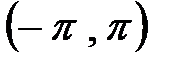 . Для этого вычислим несколько интегралов
. Для этого вычислим несколько интегралов
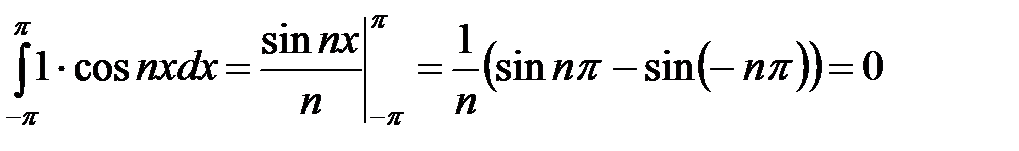 ,
,
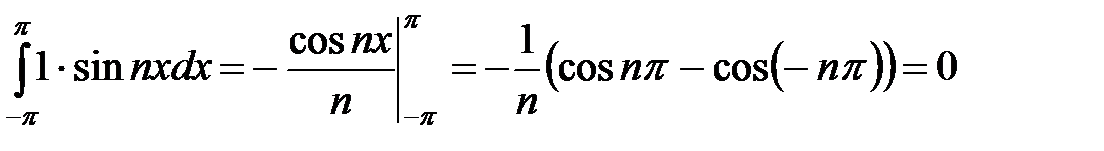 ,
,
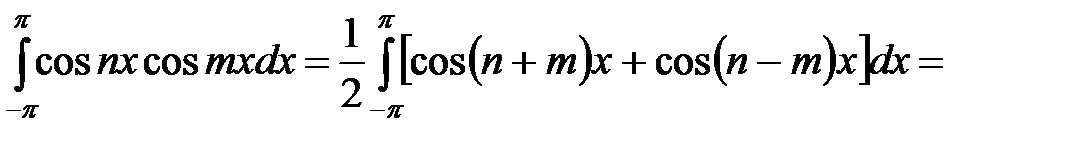
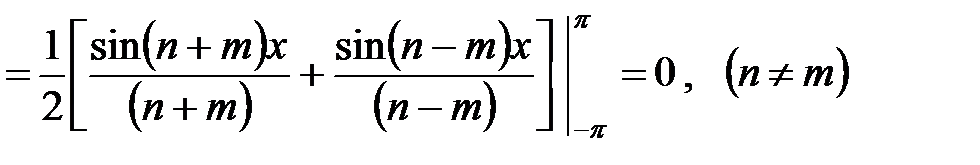 ,
,
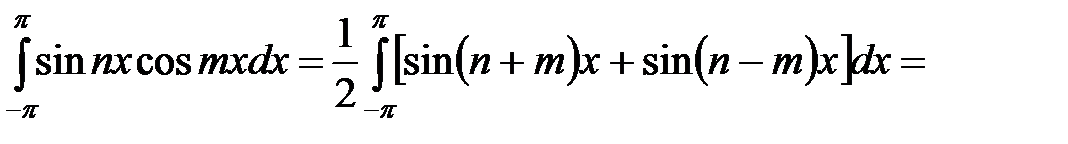

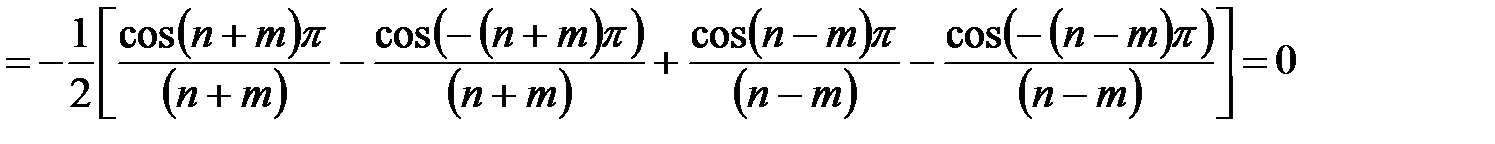 ,
,
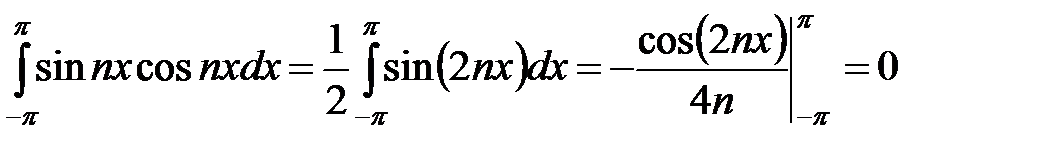 ,
,
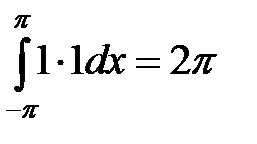 ,
,  ,
,
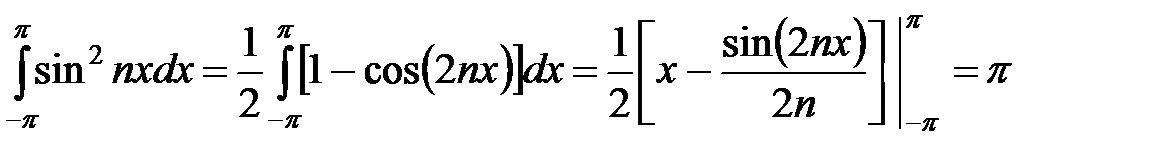 .
.
Итак, доказано, что интегралы от произведений разных функций этой системы равны нулю, интегралы от произведений одинаковых функций равны 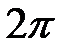 и
и 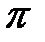 . Ортогональность системы функций доказана.
. Ортогональность системы функций доказана.
Определение 2. Система функций является полной в заданном промежутке, если нет ни одной, не входящей в эту систему, функции, кроме функции, тождественно равной нулю, ортогональной функциям системы.
Например, система косинусов 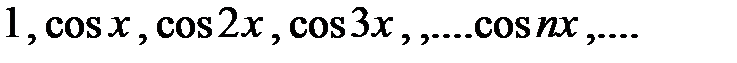 не обладает полнотой, так как любой
не обладает полнотой, так как любой 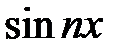 ортогонален и к 1, и ко всем функциям
ортогонален и к 1, и ко всем функциям 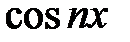 . Следствием этого является то, что в ряды по косинусам можно разлагать не все, а только четные функции. По той же причине не обладает полнотой и система синусов
. Следствием этого является то, что в ряды по косинусам можно разлагать не все, а только четные функции. По той же причине не обладает полнотой и система синусов  , что позволяет разлагать в ряд Фурье по синусам только нечетные функции. Доказательство полноты достаточно сложно, поэтому ограничимся утверждением, что вышеприведенная система тригонометрических функций полна.
, что позволяет разлагать в ряд Фурье по синусам только нечетные функции. Доказательство полноты достаточно сложно, поэтому ограничимся утверждением, что вышеприведенная система тригонометрических функций полна.
Полнота системы функций обеспечивает единственность разложения в ряд Фурье (представления в виде ряда Фурье) любой, удовлетворяющей некоторым условиям, функции, что весьма ценно при решении с помощью рядов Фурье всевозможных уравнений.
Определение 3. Если функция в некоторой области имеет конечное число точек разрыва первого рода (конечные разрывы), а между этими точками она непрерывна, такая функция называется кусочно-непрерывной.
Определение 4. Если в некоторой области функция имеет конечное число точек, между которыми она дифференцируема, а в самих этих точках существуют конечные значения левых и правых пределов, как самой функции, так и ее производной, то она называется кусочно-дифференцируемой в этой области.
Теорема. Для любой кусочно-дифференцируемой, периодической с периодом 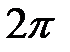 функции
функции 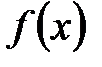 ее ряд Фурье сходится, а его сумма равна
ее ряд Фурье сходится, а его сумма равна

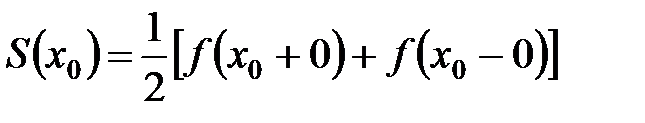 ,
,
здесь 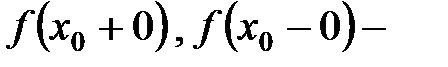 правый и левый пределы функции
правый и левый пределы функции 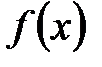 при
при 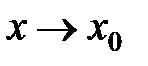 (теорема приводится без доказательства).
(теорема приводится без доказательства).
Следствие. Сумма ряда равна 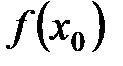 , если функция непрерывна.
, если функция непрерывна.
Известно, что ряд Фурье, представляющий разложение 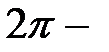 периодической непрерывной функции, сходится равномерно.
периодической непрерывной функции, сходится равномерно.
Разложение в ряд Фурье 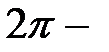 периодической функции
периодической функции
Теорема. Если 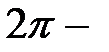 периодическая функция
периодическая функция 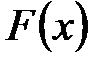 непрерывна (или кусочно-непрерывна), то значение интеграла
непрерывна (или кусочно-непрерывна), то значение интеграла 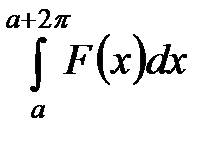 не зависит от
не зависит от 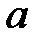 .
.
Доказательство. 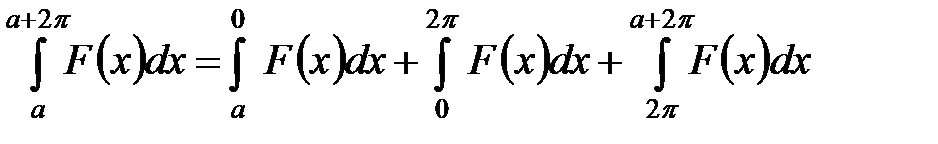 .
.
В последнем интеграле сделаем замену переменной
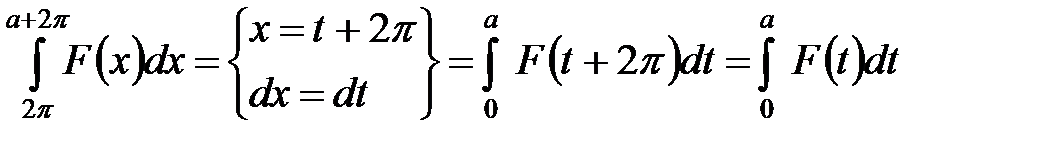 ,
,
что следует из периодичности подынтегральной функции. Тогда
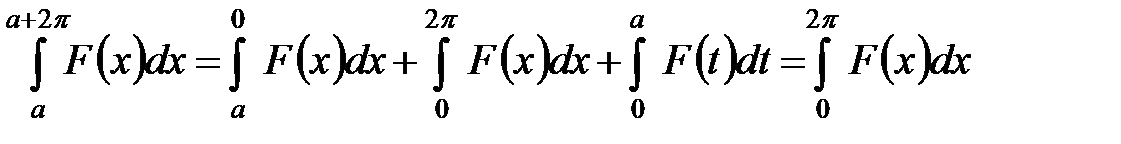 .
.
Теорема доказана, поскольку 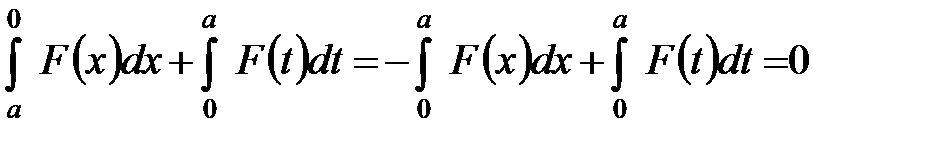 .
.
Пусть 
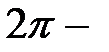 периодическая, кусочно-дифференцируемая функция, следовательно, она разложима в ряд Фурье
периодическая, кусочно-дифференцируемая функция, следовательно, она разложима в ряд Фурье
 .
.
Определим коэффициенты этого разложения, для чего умножим обе части равенства на 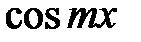 и проинтегрируем в пределах от
и проинтегрируем в пределах от 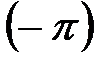 до
до 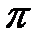 . Тогда
. Тогда
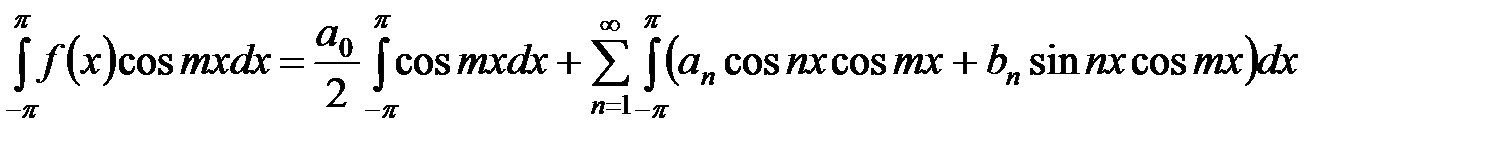 .
.
Из ортогональности системы тригонометрических функций, это было доказано выше, следует, что интеграл 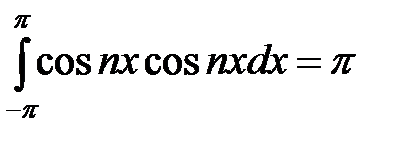 , а все остальные интегралы в правой части равенства равны нулю. В этом случае
, а все остальные интегралы в правой части равенства равны нулю. В этом случае
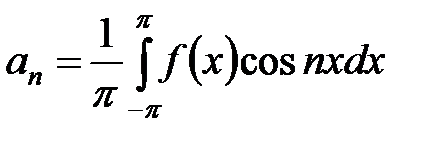 .
.
Нетрудно заметить, что полученная формула справедлива для 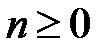 .
.
Умножим обе части исходной формулы на 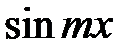 и проинтегрируем в тех же пределах
и проинтегрируем в тех же пределах
 .
.
Также из ортогональности рассматриваемых функций следует 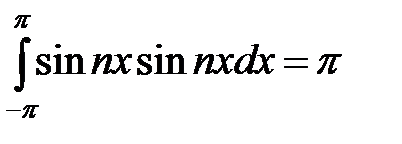 , все остальные интегралы в правой части равенства равны нулю, отсюда имеем
, все остальные интегралы в правой части равенства равны нулю, отсюда имеем
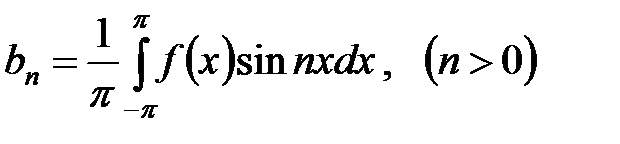 .
.
Здесь при интегрировании использовалась только что доказанная теорема.
Таким образом,
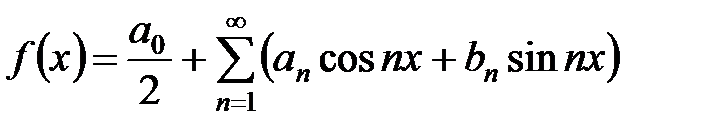 ,
,
причем 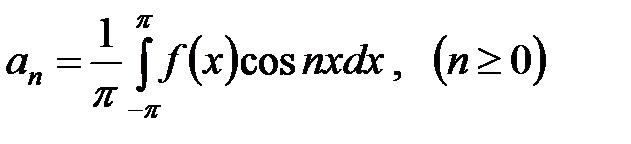 ,
, 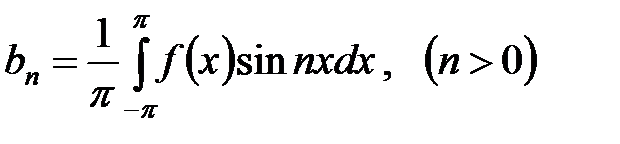 .
.
Разложение в ряд Фурье  периодической функции
периодической функции
Обобщим полученный результат на функции с периодом 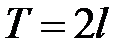 . Очевидно, такая возможность несколько расширяет область применимости рядов Фурье.
. Очевидно, такая возможность несколько расширяет область применимости рядов Фурье.
Пусть дана кусочно-дифференцируемая, периодическая с периодом 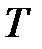 функция, то есть удовлетворяющая условию
функция, то есть удовлетворяющая условию 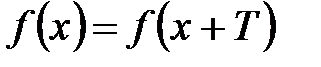 . Перейдем от переменной
. Перейдем от переменной 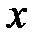 к переменной
к переменной 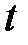 , считая при этом
, считая при этом  . Тогда функция
. Тогда функция 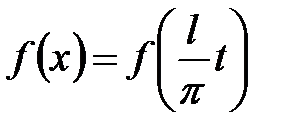 , причем
, причем  осталась периодической, но ее период стал
осталась периодической, но ее период стал 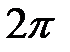 . Проверим это:
. Проверим это:
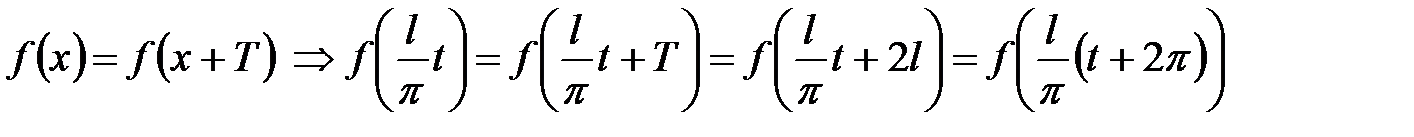 .
.
Отсюда имеем 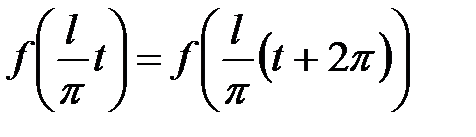 , что требовалось доказать.
, что требовалось доказать.
Теперь воспользуемся разложением в ряд Фурье  периодической функции
периодической функции
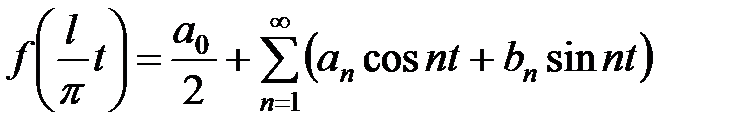 ,
,
причем 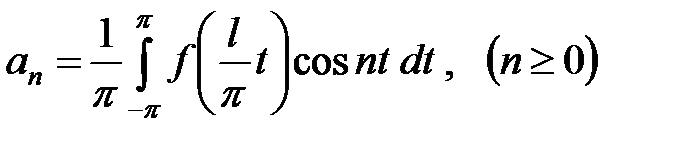 ,
,  .
.
Сделаем обратную замену  , тогда
, тогда
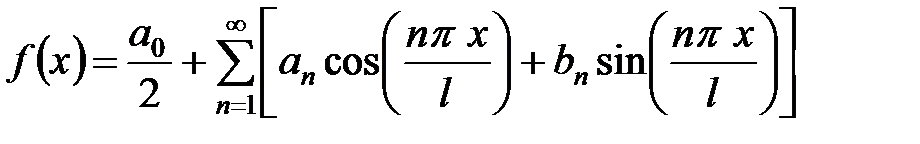 ,
,
при этом
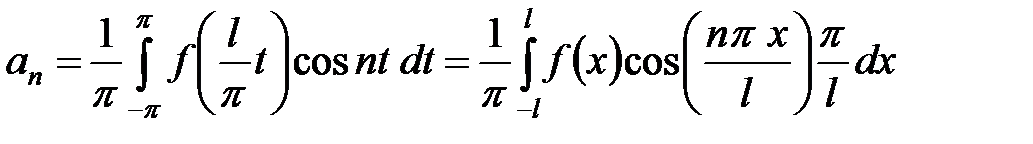 ,
,
 .
.
Таким образом,  периодическая, кусочно-дифференцируемая функция может быть представлена в виде ряда Фурье
периодическая, кусочно-дифференцируемая функция может быть представлена в виде ряда Фурье
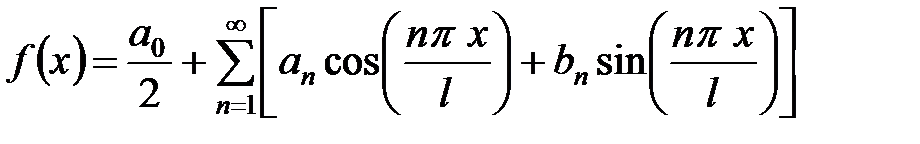 ,
,
Где
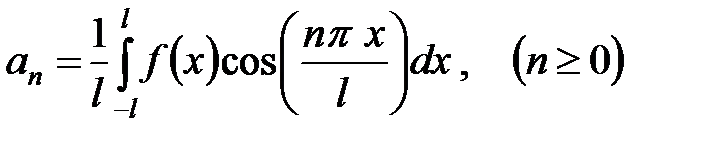 ,
, 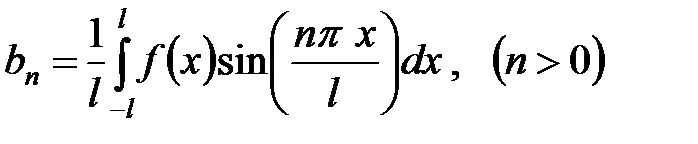 .
.
Разложение в ряд Фурье четной, или нечетной
периодической функции
Лемма 1. 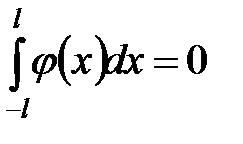 , если подынтегральная функция нечетна.
, если подынтегральная функция нечетна.
Доказательство. Очевидно, 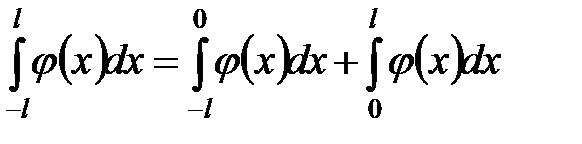 , сделаем в первом интеграле правой части замену переменной с учетом того, что
, сделаем в первом интеграле правой части замену переменной с учетом того, что 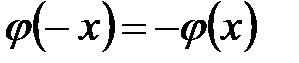 ,
,
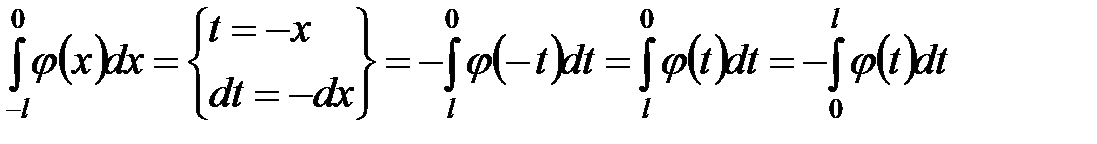 .
.
Тогда  . Доказано.
. Доказано.
Лемма 2. 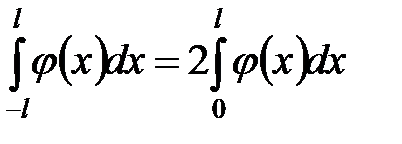 , если подынтегральная функция четна.
, если подынтегральная функция четна.
Доказательство. В первом интеграле правой части равенства 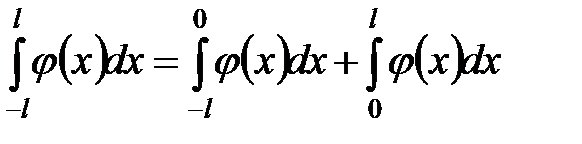 сделаем ту же замену переменной с учетом четности подынтегральной функции
сделаем ту же замену переменной с учетом четности подынтегральной функции  , тогда
, тогда
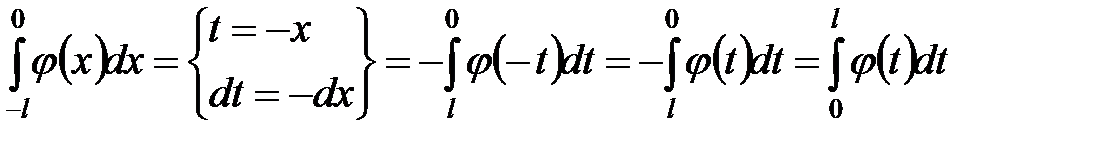 .
.
В результате