В процессе проектирования стремятся оптимизировать систему по нескольким противоречивым критериям, когда оптимизация системы по одному из критериев исключает возможность оптимизации по другим критериям. Идеологии многокритериального выбора соответствует процедура выделения множества Парето.
Множество Парето образует набор таких объектов, что переход от одного к другому обязательно повысит значение хотя бы одного критерия и ухудшит значение минимум одного критерия. Если при этом по одному или нескольким критериям один объект будет лучше другого, то говорят, что он доминирует. В множестве Парето ни один объект не доминирует над другим. Процедура нахождения множества Парето и заключается в нахождении доминирующих объектов и исключении из рассмотрения доминируемых.В таблице 2 приведены значения двух критериев, характеризующих инвестиционные проекты: прибыль и сумма капитальных вложений. Таблица 2.
| Показатель | Проект №1 | Проект №2 | Проект №3 | Проект №4 | Проект №5 | Проект №6 | Проект №7 |
| Прибыль, млн. руб. | |||||||
| Кап. вложения, млн. руб. |
Попарное сравнение проектов показывает, что проект №5 доминирует проект №2 (прибыль выше при меньших капвложениях), а проект №1 доминирует проект №3 (прибыль выше при равных капвложениях). Проекты №2 и №3исключаются из рассмотрения. Каждый из остальных проектов в каком-то смысле лучше другого оставшегося, а в каком-то хуже: или он даёт больше прибыли, но
требует больших капитальных вложений, или наоборот. Проекты 1, 4, 5, 6 и 7 оптимальны по Парето. Выбор одного из них требует дополнительных соображений.
Задачу многокритериальной максимизации записывают в следующем виде, аналогичном задаче скалярной оптимизации
ϕ(x) → max, x ∈ X, или y → max, y = ϕ(x), x ∈ X ⊆ W, ϕ: W → R m. Важно найти согласованный оптимум для всех используемых критериев. Согласованный оптимум означает преобразование конфликтной ситуации в такую, когда ни один из участников конфликта не может улучшить свое состояние, не причинив своими действиями вреда партнерам. Состояние согласованного оптимума является наилучшим для всех взаимодействующих субъектов.
Закон Парето — эмпирическое правило в наиболее общем виде формулируется как «20% усилий дают 80% результата, а остальные 80% усилий — лишь 20% результата». Это может использоваться как базовая установка в анализе эффективности: правильно выбрав минимум самых важных действий, можно получить значительную часть от планируемого полного результата, при этом дальнейшие улучшения неэффективны и могут быть неоправданными. Если x*ÎX – парето-оптимальное решение на множестве X, то не существует другого решения xÎ X, которое превосходит x* хотя бы по одному критерию, а по остальным критериям не хуже.
Пусть имеется т (т≥ 2) целевых функций, определенных на множестве X. Они образуют так называемый векторный критерий f = (f1, f2,…,fm), который принимает значения в т -мерном арифметическом
пространстве Rm. Это пространство называют критериальным пространством. Задачу выбора решений, включающую множество возможныхрешений X и векторный критерий f, называют многокритериальной задачей (или задачей векторной оптимизации).
Ключевую роль в многокритериальной оптимизации играет понятие парето-оптимального решения [8]. Парето-оптимальное решение не может быть улучшено ни по какому критерию при условии сохранения значений по всем остальным критериям.
При анализе и решении многокритериальных задач обычно считают выполненной аксиому Парето, ло которой при выполнении неравенств
fi (x’) ≥ fi (x’’) для всех номеров i = 1, 2,...,т, где по крайней мере для одного номера j выполняется строгое неравенство fi (x’) > fi (x’’), ЛПР из двух возможных решений х ' и х " отдает предпочтение первому из них. Аксиома Парето фиксирует стремление ЛПР получить максимально возможные значения по всем имеющимся критериям.
Диапазон значений оптимальных по Парето решений в области допустимых значений дает полезную информацию об исследуемой задачу если целевые функции ограничены областью определения. Нижние границы оптимальной по Парето множества представлено в «идеальном целевом векторе». Его компоненты и полученные путем минимазации каждой целевой функции в пределах области определения.
В однокритериальном случае, любые две точки x1 и x2 из допустимого множества Q всегда сравнимы: либо f(x1) ≤ f(x2), либо f(x1) > f(x2). Однако, когда целевых функций становится несколько, те. возникает векторный
критерий F[f(х)], который выполняет отображение множества допустимых
значений Х (пространство варьируемых параметров х) в некоторую область DF, то возникает вариант, когда x1 и x2 несравнимы. Формально: в пространстве входных переменных для любых двух точек x1 и x2 возможны случаи x1 ≺ x2(x1 доминирует x2) ⇐⇒f(x1) < f(x2), x1 ∼ x2(x1 безразлично x2) ⇐⇒f(x1) f(x2) ∩ f(x1) f(x2)).
Парето фронтом называется подмножество точек, для которых нет точек, их доминирующих.
Для получения оптимальных по Парето решений используют методы скаляризации. Целевую векторную функцию  задачи многокритериальной превращают в функцию со скалярным значением
задачи многокритериальной превращают в функцию со скалярным значением 
Еесли для произвольных  выполняется:
выполняется:

тогда решение 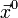 , что оптимизирует
, что оптимизирует  , является решением по Парето.
, является решением по Парето.
Парето-оптимальные коэффициенты скаляризации оиределяются на основе учёта предпочтений ЛПР.
Рассмотрим ситуацию выбора параметров создаваемого технического устройства. В простейшем случае нужно выбрать два параметра А и В, причем желательно возможно большие их значения. Подрядчик, исполнитель будущего заказа, может реализовать комбинацию
параметров,представленную кривой производственных возможностей

Рис.2. Реализуемая комбинация параметров
Предпочтения ЛПР (заказчика) выражаются, по аналогии с микроэкономико, кривой типапредельной нормы замещения MRS, которая показывает, на какое снижение параметра А заказчик готов согласиться при повышении на единицу параметра В, не меняя уровень приемлемости

Рис.3. Предпочтения заказчика

Рис.4. Выбор решения 41
Парето-оптимальный выбор -- точка V(А*, В*), поскольку эта точка доминирует всюду в пространстве под сплошной кривой MRS. К сожалению, кривую MRS не удаётся построить априорно. Но последовательно предъявляя ЛПР точки Q на кривой производственных возможностей, на основании его оценок – ΔА ~ Δ В можно реализовать алгоритм продвижения к оптимальному решению.