При рассмотрении теории интегралов, зависящих от параметра, в случае несобственных интегралов особую роль играет понятие равномерной сходимости. Выясним это понятие сначала для несобственных интегралов первого рода (НИЗП-1), затем для интегралов второго рода (НИЗП-2).
Пусть функция  определена и непрерывна на некотором прямоугольнике
определена и непрерывна на некотором прямоугольнике 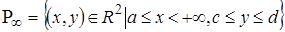 и при любом фиксированном
и при любом фиксированном 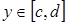 существует несобственный интеграл, зависящий от параметра, этой функции на любом промежутке
существует несобственный интеграл, зависящий от параметра, этой функции на любом промежутке  . Тогда интеграл сходится и равен
. Тогда интеграл сходится и равен
 .
.
В этом случае  называют несобственным интегралом первого рода (НИЗП-1).
называют несобственным интегралом первого рода (НИЗП-1).
Утверждение о том, что  сходится при каждом
сходится при каждом 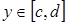 означает следующее: при каждом фиксированном
означает следующее: при каждом фиксированном 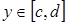
 .
.
Следовательно,
 или
или  .
.
Это значит, что для каждого 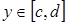 по любому
по любому  можно указать число
можно указать число  такое, что если
такое, что если  , то
, то  . Важно заметить, что
. Важно заметить, что  зависит и от
зависит и от  ,и от
,и от 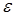 :
:  . Если же для любого
. Если же для любого  можно указать число
можно указать число  , зависящее только от
, зависящее только от 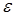 , такое, что при
, такое, что при  выполняется
выполняется 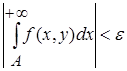 для
для 
 , то в этом случае
, то в этом случае  называется равномерно сходящимся относительно параметра
называется равномерно сходящимся относительно параметра  .
.
Теперь сформулируем критерий Коши для равномерной сходимости для нашего случая следующим образом:
Теорема 1. (критерий Коши равномерной сходимости для НИЗП-1). Для того чтобы интеграл  сходился равномерно по переменной
сходился равномерно по переменной  на промежутке
на промежутке  , необходимо и достаточно, чтобы выполнялась цепочка
, необходимо и достаточно, чтобы выполнялась цепочка
 ,
,  .
.
Рассмотрим достаточные признаки равномерной сходимости.
Теорема 2. (признак Вейерштрасса равномерной сходимости НИЗП-1). Пусть функция  определена и непрерывна на прямоугольнике
определена и непрерывна на прямоугольнике  и удовлетворяет условиям:
и удовлетворяет условиям:
1. непрерывна по переменной  ,
,
2. существует функция  , что
, что  ,
,
3.  - сходится.
- сходится.
Из этого следует, что  сходится равномерно по
сходится равномерно по  .
.
Доказательство.
В соответствии с условием 3) критерия Коши о сходимости несобственных интегралов 1-го рода от функции одной переменной имеем:
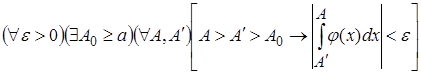 (1)
(1)
Тогда при тех же  , что и в цепочке, получаем
, что и в цепочке, получаем
 .
.
А отсюда по теореме 1 следует равномерная сходимость интеграла  .
.
Ч. т. д.
Замечание.
При выполнении условий теоремы 2 говорят, что функция  имеет интегрируемую мажоранту
имеет интегрируемую мажоранту  или что интеграл
или что интеграл  мажорируется сходящимся интегралом
мажорируется сходящимся интегралом  .
.
Следствие.
Пусть выполняются следующие условия:
1. функция  определена и непрерывна по
определена и непрерывна по  ;
;
2. функция  ограничена на прямоугольнике
ограничена на прямоугольнике  ;
;
3. интеграл  сходится, тогда следует, что
сходится, тогда следует, что 
сходится равномерно по  .
.
Обозначим через  и возьмем в качестве
и возьмем в качестве  , а в качестве функции
, а в качестве функции  . Тогда, исходя из теоремы 2, получим цепочку (1).
. Тогда, исходя из теоремы 2, получим цепочку (1).
Совершенно аналогично вводится понятие равномерной сходимости несобственных интегралов второго рода (НИЗП-2).
Пусть функция  определена в области
определена в области  (a,b,c – конечные числа). Пусть при
(a,b,c – конечные числа). Пусть при  несобственный интеграл
несобственный интеграл 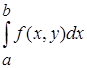 сходится. В этом случае
сходится. В этом случае 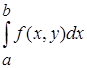 будет представлять собой функцию переменной (параметра)
будет представлять собой функцию переменной (параметра)  , определенную в промежутке
, определенную в промежутке  . Утверждение, что несобственный интеграл
. Утверждение, что несобственный интеграл  сходится при
сходится при  , означает следующее. При каждом фиксированном
, означает следующее. При каждом фиксированном  интеграл
интеграл

 (здесь
(здесь  ). Это значит, что для каждого
). Это значит, что для каждого  из
из  по любому
по любому  можно указать
можно указать  такое, что при условии
такое, что при условии 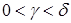 выполняется
выполняется  . Важно отметить, что число
. Важно отметить, что число  выбирается по
выбирается по  , и для каждого
, и для каждого  оно будет своим, другими словами,
оно будет своим, другими словами,  зависит и от
зависит и от  , и от
, и от  :
:  . Если же можно указать такое
. Если же можно указать такое  , зависящее только от
, зависящее только от  , такое, что при выполнении условия
, такое, что при выполнении условия  будет верно
будет верно  сразу для всех
сразу для всех  , несобственный интеграл
, несобственный интеграл  называется равномерно сходящимся относительно параметра. Короче говорят, интеграл
называется равномерно сходящимся относительно параметра. Короче говорят, интеграл  называется равномерно сходящимся по переменной
называется равномерно сходящимся по переменной  на
на  , если он сходится при
, если он сходится при  и выполняется цепочка
и выполняется цепочка  .
.
Для НИЗП-2 справедливы теоремы аналогичные т.1 и т. 2.
Теорема 3. (критерий Коши равномерной сходимости НИЗП-2). Для того чтобы НИЗП-2 равномерно сходился по  необходимо и достаточно, чтобы:
необходимо и достаточно, чтобы:
 ,
,  .
.
Теорема 4. Пусть функция  определена в области
определена в области 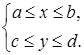
 и удовлетворяет следующим условиям:
и удовлетворяет следующим условиям:
1. функция  непрерывна по
непрерывна по  , при
, при  ;
;
2. существует такая функция  , что
, что  ,
,  и
и  .
.
3.  - сходится
- сходится 
НИЗП-2  сходится равномерно по
сходится равномерно по  на
на  .
.
Доказательство проводится аналогично доказательству теоремы 2.
Пример. Исследовать на равномерную сходимость интеграл  .
.
Для определения равномерной сходимости необходимо проверить выполнение всех условий теоремы 2.
1.  определена и непрерывна в области
определена и непрерывна в области  ;
;
2. существует функция  ,
,  , для любого
, для любого  ;
;
3.  , то есть сходится.
, то есть сходится.
Так как все условия выполнены, то интеграл  сходится равномерно относительно
сходится равномерно относительно  на любом промежутке
на любом промежутке  .
.