Глава 1. Собственные интегралы, зависящие от параметра
Пункт 1. Понятие интеграла, зависящего от параметра
Для того чтобы дать определение интеграла, зависящего от параметра, введем функцию  . Пусть эта функция
. Пусть эта функция  будет определена на некотором множестве
будет определена на некотором множестве  , где
, где  и
и  , то есть в результате получится множество
, то есть в результате получится множество  . Если функция
. Если функция  непрерывна в D, то тогда имеет смысл интеграл
непрерывна в D, то тогда имеет смысл интеграл  , где x принадлежит некоторому конечному или бесконечному промежутку
, где x принадлежит некоторому конечному или бесконечному промежутку  , значит, интеграл может быть несобственным.
, значит, интеграл может быть несобственным.
На основании этого можно дать определение интеграла, зависящего от параметра.
Определение.
Интеграл  называется интегралом, зависящим от параметра, если
называется интегралом, зависящим от параметра, если  интегрируема на промежутке
интегрируема на промежутке  при любом фиксированным
при любом фиксированным  , где
, где 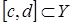 .
.
Следовательно,  представляет собой функцию
представляет собой функцию  переменной (параметра)
переменной (параметра)  , определенную в промежутке
, определенную в промежутке  . Возможно также существование интеграла при фиксированном
. Возможно также существование интеграла при фиксированном  , тогда он будет представлять собой функцию переменной (параметра)
, тогда он будет представлять собой функцию переменной (параметра) 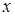 , определенную в промежутке
, определенную в промежутке  . Обозначается она так
. Обозначается она так  , так что
, так что  .
.
Основная задача будет состоять в том, чтобы, зная свойства функции  , получить информацию о свойствах функции
, получить информацию о свойствах функции  . Эти свойства имеют многообразные применения, особенно при вычислении несобственных интегралов.
. Эти свойства имеют многообразные применения, особенно при вычислении несобственных интегралов.
Пример. Найти интеграл  от функции
от функции  ,
, 
Функция  непрерывна на отрезке
непрерывна на отрезке  при любом фиксированном
при любом фиксированном  , а значит, она интегрируема. Тогда
, а значит, она интегрируема. Тогда
 .
.
Пункт 2. Предельный переход под знаком интеграла. Непрерывность интеграла как функции параметра
Определение.
Пусть  - это предельная точка множества
- это предельная точка множества 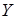 .Функция
.Функция  называется равномерно сходящейся к функции
называется равномерно сходящейся к функции  при
при  по переменной
по переменной  , если выполняются следующие условия:
, если выполняются следующие условия:
1. для  при
при  существует конечная предельная функция
существует конечная предельная функция  ;
;
2.  . (1)
. (1)
Замечание 1.
В цепочки (1)  зависит только от
зависит только от  и не зависит от
и не зависит от 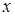 , а неравенство
, а неравенство  выполняется при любых
выполняется при любых  одновременно.
одновременно.
Замечание 2.
Если  , то в цепочке (1) неравенство
, то в цепочке (1) неравенство  следует заменить на
следует заменить на  (
( ).
).
Теорема 1 (признак сходимости). Если функция  определена на множестве
определена на множестве 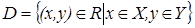 , то для того, чтобы она имела предельную функцию и сходилась к ней равномерно необходимо и достаточно, чтобы выполнялась цепочка
, то для того, чтобы она имела предельную функцию и сходилась к ней равномерно необходимо и достаточно, чтобы выполнялась цепочка
 Докажем теорема так.
Докажем теорема так.
Необходимость. Пусть функция  равномерно сходится. Если заменим в определении
равномерно сходится. Если заменим в определении  на
на  и выберем соответственно
и выберем соответственно  , а затем возьмем два значения
, а затем возьмем два значения  и
и  из
из 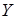 так, чтобы выполнялись условия
так, чтобы выполнялись условия  и
и 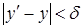 . В результате получим
. В результате получим 
 и
и  откуда следует последнее неравенство в цепочке
откуда следует последнее неравенство в цепочке  .
.
Достаточность. Теперь пусть существует предельная функция  . Нужно доказать равномерную сходимость функции
. Нужно доказать равномерную сходимость функции  к предельной функции. Для этого совершим переход к пределу в неравенстве
к предельной функции. Для этого совершим переход к пределу в неравенстве  при
при  , получается
, получается 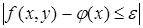 . Что и подтверждает равномерную сходимость
. Что и подтверждает равномерную сходимость  к функции
к функции  .
.
Теорема 2 (о непрерывности предельной функции). Если функция  при любом фиксированном
при любом фиксированном  непрерывна на
непрерывна на 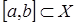 и равномерно сходится к предельной функции
и равномерно сходится к предельной функции  по переменной
по переменной 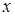 при
при  , то функция
, то функция  также непрерывна на
также непрерывна на  .
.
Легко обобщается теорема Дини: если функция  непрерывна для любого фиксированного
непрерывна для любого фиксированного  на
на 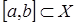 и при возрастании
и при возрастании  функция, монотонно возрастая, стремится к предельной функции
функция, монотонно возрастая, стремится к предельной функции  , то
, то  сходится к
сходится к  равномерно.
равномерно.
Теорема 3 (предельный переход по параметру под знаком интеграла). Если функция  непрерывна при постоянном значении
непрерывна при постоянном значении  на
на  и сходится равномерно по переменной
и сходится равномерно по переменной 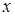 к предельной функции
к предельной функции  при
при  , то тогда имеет место равенство
, то тогда имеет место равенство
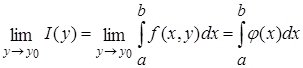 (2)
(2)
Доказательство.
Непрерывность  следует из теоремы 2, значит, она интегрируема на отрезке
следует из теоремы 2, значит, она интегрируема на отрезке  . В силу равномерной сходимости
. В силу равномерной сходимости  к
к  выполняется
выполняется  . Тогда при тех же
. Тогда при тех же  и
и  имеем:
имеем:
 откуда следует
откуда следует 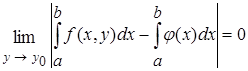 , что доказывает формулу (2).
, что доказывает формулу (2).
Замечание 3.
Равенство (2) можно записать и в другом виде
 . (2`)
. (2`)
Следствие 1.
Если функция  при постоянном
при постоянном  непрерывна по
непрерывна по  и при возрастании
и при возрастании  стремится, монотонно возрастая, к непрерывной предельной функции
стремится, монотонно возрастая, к непрерывной предельной функции  , то справедливы формулы (2) и (2`).
, то справедливы формулы (2) и (2`).
В предположении, что область  представляет собой конечный промежуток
представляет собой конечный промежуток  , рассмотрим вопрос о непрерывности функции
, рассмотрим вопрос о непрерывности функции  .
.
Пример (№3713 (в)). Найти 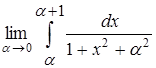 .
.
1. функция  непрерывная функция на
непрерывная функция на 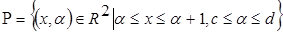 . Функции
. Функции  и
и  также непрерывны на
также непрерывны на  .
.
2.  непрерывная функция (т.4 и сл.2) в промежутке
непрерывная функция (т.4 и сл.2) в промежутке  , значит
, значит 
3.  .
.
Теорема 4 (о непрерывности интеграла как функции параметра). Пусть функция  определена и непрерывна в прямоугольнике
определена и непрерывна в прямоугольнике  , тогда интеграл
, тогда интеграл  будет непрерывной функцией от параметра
будет непрерывной функцией от параметра  в промежутке
в промежутке  .
.
Доказательство.
Так как  непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на данном прямоугольнике
непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на данном прямоугольнике  . Возьмем любое
. Возьмем любое  и зафиксируем
и зафиксируем  . Тогда нашему значению
. Тогда нашему значению  будет соответствовать
будет соответствовать  , такое, что для любых двух точек
, такое, что для любых двух точек  ,
,  принадлежащих
принадлежащих 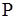 , из неравенств
, из неравенств  и
и  , будет следовать
, будет следовать  . Положим
. Положим 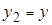 ,
,  , где
, где  ,
,  - любые из
- любые из  , и
, и  , где
, где  . Тогда получим
. Тогда получим
 . Это означает, что функция
. Это означает, что функция  равномерно стремится к
равномерно стремится к  . В таком случае по теореме 3
. В таком случае по теореме 3  , а уже отсюда следует равенство
, а уже отсюда следует равенство  , то есть наша функция
, то есть наша функция  непрерывна на
непрерывна на  .
.
Замечание 4. Совершенно аналогично доказывается теорема для  , где
, где  .
.
Следствие 2. Если  непрерывна на прямоугольнике
непрерывна на прямоугольнике 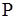 , то
, то  .
.
Пример. Найти 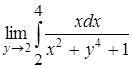 .
.
1.  непрерывна на
непрерывна на 
2. тогда по теореме 4. и следствию 2 получаем
