| Определение: |
Подмножество  вершин графа вершин графа  называется независимым, если любые две вершины из называется независимым, если любые две вершины из  не смежны в не смежны в 
|
| Определение: |
Число независимости  графа графа  — —  и и  независимо в G независимо в G 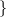
|
| Лемма (нижняя оценка): |
Пусть  — произвольный связный неориентированный граф с — произвольный связный неориентированный граф с 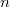 вершинами.Тогда, вершинами.Тогда,  . .
|
| Доказательство: |

|
Пусть,  множеств вершин окрашенных в соответствующие цвета при правильно покраски графа множеств вершин окрашенных в соответствующие цвета при правильно покраски графа  .Каждое из .Каждое из  — независимое множество (поскольку вершины множества покрашены в один цвет при правильной покраски графа — независимое множество (поскольку вершины множества покрашены в один цвет при правильной покраски графа  , следовательно, они попарно не смежны внутри множества).
Заметим, что для произвольного , следовательно, они попарно не смежны внутри множества).
Заметим, что для произвольного  , ,  (т.к (т.к  независимое множество). То есть, независимое множество). То есть, 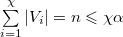 , следовательно , следовательно 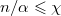 . .
|
8.2 Конструирование хроматического полинома
| Теорема (Зыкова): |
Для хроматического многочлена графа  верна формула: верна формула:  , где , где  — число способов разбить вершины — число способов разбить вершины  на на  независимых множеств, независимых множеств,  , а , а  — нисходящая факториальная степень. — нисходящая факториальная степень.
|
| Доказательство: |

|
В правильной раскраске вершины, имеющие одинаковый цвет, не смежны, поэтому все такие вершины могут быть объединены в одно независимое множество. Перебрав все возможные разбиения на независимые множества с последующей их всевозможной покраской  доступными цветами получим искомое число способов раскраски графа доступными цветами получим искомое число способов раскраски графа  в в  цветов.
Теперь проделаем это более формально. Подсчитаем число раскрасок графа цветов.
Теперь проделаем это более формально. Подсчитаем число раскрасок графа  , в которых используется точно , в которых используется точно  цветов, для этого его нужно разбить на цветов, для этого его нужно разбить на  независимых множеств и вершины в каждом таком классе покрасить в один из независимых множеств и вершины в каждом таком классе покрасить в один из  цветов, отличный от всех других множеств, так как мы не делаем никаких предположений о связи между классами.
Рассмотрим случай, где цветов, отличный от всех других множеств, так как мы не делаем никаких предположений о связи между классами.
Рассмотрим случай, где  . Чтобы получить такую раскраску зафиксируем какое-нибудь разбиение множества вершин графа . Чтобы получить такую раскраску зафиксируем какое-нибудь разбиение множества вершин графа  на на  независимых множеств, затем берем один из классов в разбиении и раскрашиваем его в один из независимых множеств, затем берем один из классов в разбиении и раскрашиваем его в один из  цветов, потом берем следующий класс и окрашиваем его вершины в одинаковый цвет любой из цветов, потом берем следующий класс и окрашиваем его вершины в одинаковый цвет любой из  оставшихся красок и т.д. Всего таких способов разбиения существует оставшихся красок и т.д. Всего таких способов разбиения существует  . Следовательно, перебрав все возможные разбиения на . Следовательно, перебрав все возможные разбиения на  независимых множеств, получим, что число интересующих нас раскрасок графа независимых множеств, получим, что число интересующих нас раскрасок графа  равно равно 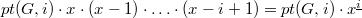 .
Заметим теперь, что при .
Заметим теперь, что при  число число  -раскрасок, в которых используется точно -раскрасок, в которых используется точно  цветов, равно цветов, равно 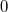 и при этом и при этом  тоже равно тоже равно 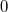 .
Суммирование по .
Суммирование по  от от 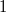 до до 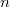 даст полное число способов. даст полное число способов.
|
https://www.allmath.ru/highermath/algebra/graph/graph5.htm
8.3 Теорема Кёнига о бихроматических графах
| Теорема: |
Граф  -раскрашиваемый тогда и только тогда, когда он двудольный. -раскрашиваемый тогда и только тогда, когда он двудольный.
|
| Доказательство: |

|
Если множество вершин двудольного графа можно разделить на два независимых подмножества так, что ни одна из вершин ни в одном из этих подмножеств не является смежной к вершине из этого же подмножества, тогда граф  — —  -раскрашиваем. -раскрашиваем.  .
Если же граф .
Если же граф  -раскрашиваемый, то множество его вершин можно разделить на два непересекающихся множества так, чтобы в каждом из них не нашлось двух смежных вершин. Тогда граф будет двудольны. -раскрашиваемый, то множество его вершин можно разделить на два непересекающихся множества так, чтобы в каждом из них не нашлось двух смежных вершин. Тогда граф будет двудольны.
|
8.4 Алгоритм построения правильной раскраски.


8.5 Теорема Хивуда о раскраске планарного графа
https://kadm.imkn.urfu.ru/files/tgr13.pdf
8.6 Раскраска карт.
Теорема о четырёх красках утверждает, что всякую расположенную на сфере карту можно раскрасить не более чем четырьмя разными цветами (красками) так, чтобы любые две области с общим участком границы были раскрашены в разные цвета. При этом области могут быть как односвязными, так и многосвязными (в них могут присутствовать «дырки»), а под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке не считаются общей границей для них. Задача раскраски карты на плоскости эквивалентна задаче на сфере.
8.7 Теоремы Шеннона и Визинга о хроматическом классе.
Теорема Визинга — утверждение теории графов, согласно которому рёбра любого неориентированного графа могут быть раскрашены в число цветов, максимум на единицу большего максимальной степени вершин А δ {\displaystyle \delta } графа. Поскольку по меньшей мере А δ {\displaystyle \delta } цветов необходимо всегда, все неориентированные графы можно разбить на два класса — графы «первого класса», для которых А δ {\displaystyle \delta } цветов достаточно, и «второго класса», для которых необходимо А+1 δ + 1 {\displaystyle \delta +1} цветов.
Результат установлен Вадимом Визингом в 1964 году.
https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%92%D0%B8%D0%B7%D0%B8%D0%BD%D0%B3%D0%B0#.D0.90.D0.BB.D0.B3.D0.BE.D1.80.D0.B8.D1.82.D0.BC.D1.8B
https://ru.wikipedia.org/wiki/%D0%9C%D1%83%D0%BB%D1%8C%D1%82%D0%B8%D0%B3%D1%80%D0%B0%D1%84_%D0%A8%D0%B5%D0%BD%D0%BD%D0%BE%D0%BD%D0%B0#CITEREFShannon1949