Расстояние между параллельными плоскостями
Плоскость α и плоскость β параллельны. На плоскости β выберем произвольную точку А (рис. 2). Из точки А опустим перпендикуляр АА0 на плоскость α. Перпендикуляр АА0 и назовем расстоянием между плоскостями α и β.
Заметим, что длина этого перпендикуляра не зависит от того, какую точку мы выбрали.
Например, выберем другую точку В, опустим перпендикуляр ВВ0. Прямые АА0 и ВВ0 перпендикулярны одной и той же плоскости, значит, прямые АА0 и ВВ0 параллельны. Тогда из свойств параллельных плоскостей отрезки АА0 и ВВ0 равны.
Расстояние между прямой и плоскостью
Расстояние между прямой и плоскостью определяется в случаях, когда прямая параллельна плоскости. Тогда все точки прямой а равноудалены от плоскости α. Выберем любую точку А на прямой а, опустим перпендикуляр АА0 на плоскость α (рис. 3). Длина перпендикуляра АА0 и называется расстоянием между прямой а и параллельной ей плоскостью α.
Обозн.: АА0 = р(а; α ).
Вопрос 2. Перпендикуляр и наклонная
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
Конец отрезка, лежащий в плоскости, называется основанием наклонной (Рис. 4).
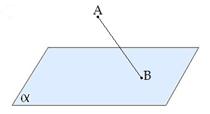
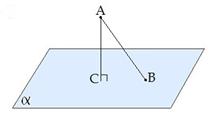
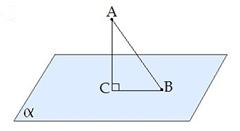
Рис. 4 Рис. 5 Рис. 6
AB - наклонная.
B - основание наклонной.
AC - перпендикуляр.
C - основание перпендикуляра.
CB - проекция наклонной AB на плоскость α.
Перпендикуляром, проведенным из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости.
Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра (Рис. 5).
Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к плоскости.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной (Рис. 6).
Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость.
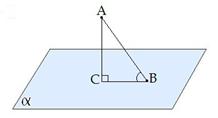
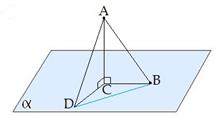
Рис. 7 Рис. 8
∢CBA - угол между наклонной AB и плоскостью α (Рис. 7).
Если AD>AB, то DC>BC (Рис. 8).
Если из данной точки к данной плоскости провести несколько наклонных, то большей наклонной соответствует большая проекция.
Решение задач из учебника. https://docbaza.ru/urok/geometr/10/007/044.html
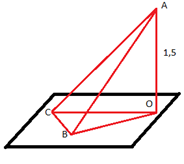
140. Из точки А, не принадлежащей плоскости α, проведены к этой плоскости перпендикуляр АО и две наклонные АВ и АС. Известно, что ∠OAB= ∠BAС = 60°, АО = 1,5 см. Найдите расстояние между основаниями наклонных.
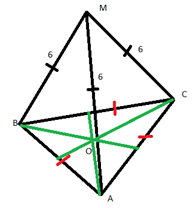
143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 см. Найдите расстояние от точки М до плоскости ABC, если АВ = 6 см.
Вопрос 3. Теорема о трех перпендикулярах.
Теорема о трех перпендикулярах. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной (рис. 9).
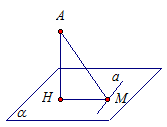
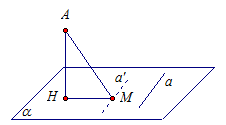
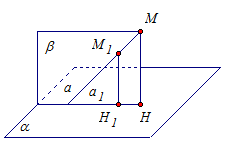
Рис. 9. Рис. 10. Рис. 11.
Обратная теорема
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Замечание к теореме о трех перпендикулярах
В доказанной прямой и обратной теореме точка М (основание наклонной) лежала на прямой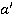 
, лежащей в плоскости α. Давайте проведем в плоскости α другую прямую а, которая параллельна 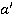. Тогда углы между прямыми a, АМ, НМ не изменятся. И из перпендикулярности прямой а и прямой АМ будет вытекать перпендикулярность прямой а и прямой НМ и наоборот.
Проекция фигур на плоскость
Любая фигура, в том числе фигура F, состоит из точек. Если мы все точки спроектируем на плоскость α, то получим фигуру F1 – проекцию фигуры F на плоскость α. F1 = пр α F (рис. 10).
Утверждение о проекции прямой на плоскость, не перпендикулярной плоскости
Проекцией прямой а на не перпендикулярную к ней плоскость α является прямая (рис. 11).
Вопрос 4. Угол между прямой и плоскостью.
Определение. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярную к ней, называется угол между прямой и ее проекцией на плоскость.
Рис. 4.
Рассмотрим плоскость α и прямую АН, НМ - перпендикуляр, АМ - проекция прямой. Угол между прямой АН и плоскостью α – это угол между прямой АН и ее проекцией АМ на плоскости, т.е. это угол МАН = φ0. Обозначение: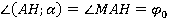 
Если прямая перпендикулярна плоскости, то она проектируется в точку, угол между прямой и плоскостью считается равным 90°.