Средства измерений уравновешивающего преобразования

Структурная схема средства измерений уравновешивающего преобразования показана на рис. 1.3.

Рис. 1.3. Структурная схема средства измерений уравновешивающего преобразования

Для цепи обратного преобразования (обратной связи)

x_m^` = x_nβ₁ β₂ …. β_m = x_nβ (1.5)

где β — коэффициент преобразования цепи обратного преобразования;

β₁, β₂,.., β_m — коэффициенты преобразования звеньев обратной связи.

На входе цепи прямого преобразования в узле СУ происходит сравнение (компенсация) входного сигнала х и выходного сигнала цепи обратного преобразования х'_m и при этом на выходе СУ получается разностный сигнал Δх = х — х'_m.

При подаче на вход сигнала х выходной сигнал х_n, а следовательно, и х'_m, будут возрастать до тех пор, пока х и х'_т не станут равны. При этом по значению х_n можно судить об измеряемой величине х.

Средства измерений, имеющие такую структурную схему, могут работать как с полной, так и с неполной компенсацией.

При полной компенсации в установившемся режиме

Δх = х — х_т = 0. (1.6)

Это возможно в тех устройствах, у которых в цепи прямого преобразования предусмотрено интегрирующее звено с характеристикой преобразования х_i= (x_i-1) dt. Примером такого звена является электродвигатель, для которого угол поворота вала определяется приложенным напряжением и временем. В этом случае, учитывая (1.5) и (1.6), получим

х_n = х/(β₁ β₂... β_m)=х/ β. (1.7)

Таким образом, в момент компенсации сигнал на выходе средства измерений пропорционален входному сигналу и не зависит от коэффициента преобразования цепи прямого преобразования.

Чувствительность (коэффициент преобразования)

S= = = 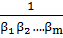(1.8)

Мультипликативная относительная погрешность, обусловленная нестабильностью коэффициентов преобразования звеньев, при достаточно малых изменениях этих коэффициентов

Как видно из этого выражения, относительная мультипликативная погрешность обусловлена только относительным изменением коэффициента преобразования цепи обратного преобразования.

Аддитивная погрешность в средствах измерений с полной компенсацией практически обусловливается порогом чувствительности звеньев, расположенных до интегрирующего звена, и порогом чувствительности самого интегрирующего звена.

Под порогом чувствительности звена понимается то наименьшее изменение входного сигнала, которое способно вызвать появление сигнала на выходе звена. Порог чувствительности имеют, например, электродвигатели, часто применяемые в рассматриваемых устройствах. Для реальных звеньев график характеристики преобразования может иметь вид, показанный на рис. 1.4, где ± Δх_i-1 — порог чувствительности.

Рис. 1.4. Характеристика преобразования звена с порогом чувствительности

При наличии порога чувствительности средства измерений состояние компенсации наступает при х — х'_т = Δх. Таким образом, изменение входного сигнала в пределах ± Δx не вызывает изменения выходного сигнала, т. е. появляется абсолютная аддитивная погрешность, значение которой может быть в пределах ± Δх.

При неполной компенсации в средствах измерений интегрирующего звена нет и обычно выполняется условие (1.5), а также

x_n = kΔx, (1.9)

где k = k₁ k₂...k_n — коэффициент преобразования цепи прямого преобразования. В этом случае установившийся режим наступает при некоторой разности

Δх = х — х'_т. (1.10)

Зависимость между выходным и входным сигналами, находимая путем решения уравнений (1.5), (1.9) и (1.10),

x_n = kx/(l+kβ). (1.11)

Как видно из выражения (1.11), при установившемся режиме выходной сигнал пропорционален входному и зависит от коэффициентов преобразования цепи как обратного, так и прямого преобразования.

Если выполняется условие kβ »l, то уравнение (1.11) переходит в (1.7) и при этом нестабильность коэффициента преобразования цепи прямого преобразования не влияет на работу устройства. Практически, чем выше kβ, тем меньше влияние k. Предел увеличения kβ обусловлен динамической устойчивостью средства измерений.

Чувствительность (коэффициент преобразования) средства измерений с неполной компенсацией

S= = (1.12)

Мультипликативная погрешность, обусловленная изменением коэффициентов преобразования звеньев при достаточно малых изменениях этих коэффициентов.

Следовательно, при kβ >>1 (что обычно имеет место) составляющая, обусловленная изменением коэффициента β, целиком входит в результирующую погрешность, а составляющая, обусловленная изменением коэффициента k, входит в результирующую погрешность ослабленной в kβ раз.

Нелинейность характеристики преобразования цепи прямого преобразования можно рассматривать как результат влияния изменения коэффициента преобразования k относительно некоторого начального значения при х = 0. Полученные уравнения показывают, что нелинейность характеристики преобразования уменьшается действием отрицательной обратной связи в kβ раз.

Аддитивная погрешность может быть найдена путем введения в структурную схему дополнительных сигналов Δx_o1, Δх_о2,-.., Δx_on, Δx`<sub>o1</sub>, Δх`_o2,..., Δх`_oт, равных смещениям характеристик преобразования соответствующих звеньев.

Применяя методику, рассмотренную выше, получим абсолютную аддитивную погрешнось, равную погрешности

Δx_o=[Δx_o1/k₁ + Δx_o1/(k₁k₂) +…. + Δx_o1/(k₁ k₂...k_n)]— (β₂β₃….β_mΔx`<sub>o1</sub> + β<sub>3</sub>β4…..β<sub>m</sub>Δx`_o2 + …+ Δx`_om). (1.13)

Следует отметить, что средства измерений могут иметь комбинированные структурные схемы, когда часть цепи преобразования охвачена обратной связью.

Вид структурной схемы средства измерений влияет не только на рассмотренные характеристики (чувствительность, погрешность), но также на входные и выходные сопротивления, динамические свойства и др.