Вэтих вольтметрах (рис. 2, а и б) измеряемое напряжение Ux предварительно преобразуется во временной интервал tx путем сравнения Ux с линейно-изменяющимся напряжением Uk.
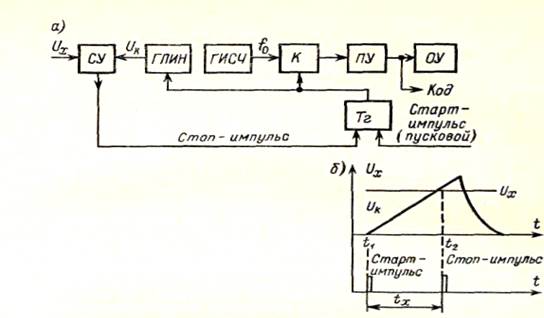
Рис. 2. Схема (а) и диаграммы напряжений (б) время-импульсного вольтметра
При запуске прибора старт-импульсом в момент t1 срабатывает триггер Тг, который открывает ключ К и запускает генератор линейно-изменяющегося напряжения ГЛИН. Напряжение UK на выходе генератора ГЛИН начинает изменяться по линейному закону, и на вход ПУ подаются квантующие импульсы. В момент t2 при UK=UX сравнивающее устройство СУ стоп-импульсом через триггер и ключ прекращает подачу импульсов в ПУ. Таким образом, за время tx=t2 — t1 = Ux/k (где k — коэффициент, характеризующий скорость изменения напряжения Uк) на вход ПУ пройдет число импульсов
N=tx/T0=Uxf0/k. (2.1)
Составляющие погрешности прибора:
1) погрешность квантования, зависящая от tx/To;
2) погрешность реализации от нестабильности fо;
3) погрешность от наличия порога срабатывания СУ;
4)погрешность от нелинейности и нестабильности кривой линейно-изменяющегося напряжения, т. е. от непостоянства k; эта составляющая практически определяет точность этих вольтметров.
В настоящее время у время-импульсных ЦИУ погрешность снижена до ±0,05 %. Показания этих ЦИУ определяются мгновенным размером входного сигнала, а поэтому эти ЦИУ чувствительны к помехам.
Задача 1.14
Найти результат и погрешность косвенного измерения частоты по результатам прямых измерений реактивного сопротивления и индуктивности катушки с независимыми случайными погрешностями, распределенными по нормальному закону.
XL = (1,10  0,02) Ом, PxL = 0,96;
0,02) Ом, PxL = 0,96;
L = (105  2) мГн, РL = 0,94.
2) мГн, РL = 0,94.
Записать результат в стандартной форме для Р = 0,92.
Решение:
1) Определяем результат косвенного измерения частоты по формуле
ω = 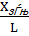 =
= 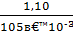 = 10,476 (Гц)
= 10,476 (Гц)
2) Определяем СКО случайной погрешности косвенного измерения σ(Y).
Для этого сначала находим СКО погрешности измерений XL и L:
σ(XL)=  ,
,
где Δ1 = 0,02 Ом – половина доверительного интервала случайной погнрешности измерения реактивного сопротивления катушки;
Z1 – значение аргумента Z для функции Лапласа
Ф(Z)= 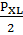 =
= 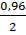 = 0,48;
= 0,48;
По таблице П.1 приложения для Ф(Z)=0,48 находим ZXL = 2,05
Отсюда
σ(XL)= 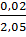 = 0,00976 Ом.
= 0,00976 Ом.
Аналгогично для нахождения σ(L) определяем Ф(Z)= 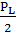 =
=  = 0,47
= 0,47
По таблице П.1 приложения для Ф(Z)=0,47 находим ZL = 1,87.
Отсюда
σ(L)=  = 0,00106 Гн.
= 0,00106 Гн.
Затем определяем частные производные:
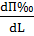 =
= 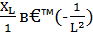 = -
= - 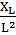 = -
= - 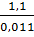 = -100.
= -100.
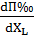 =
=  =
= 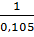 = 9,524.
= 9,524.
Наконец, находим СКО
σ(ω) = 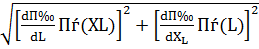 =
=
 = 0,9761 Гц.
= 0,9761 Гц.
3) Определим доверительный интервал для погрешности косвенного измерения частоты.
Для Ф(Z) = 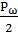 =
= 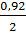 = 0,46 по таблице П.1 приложения находим Zω= 1,75.
= 0,46 по таблице П.1 приложения находим Zω= 1,75.
Отсюда
Δω= σ(ω) · Zω= 0,9761·1,75 ≈ 1,71 Гц.
4) Записываем результат измерения в стандартной форме:
ω = (10,476  1,71) Гц; Р = 0,92.
1,71) Гц; Р = 0,92.
Задача 4.07
Измерительный мост собран по схеме, приведенной на рисунке 4.1. Определить емкость конденсатора Сх и тангенс угла диэлектрических потерь tgδ, если баланс моста достигается при значениях R2, R3, R4, С3, указанных ниже, а частота питающего мост переменного напряжения f.
f = 700Гц;
С3= 2000 пФ = 2000·10-12 Ф;
R2 = 40 кОм = 40·103 Ом;
R3 = 40 кОм = 40·103 Ом;
R4 = 20 кОм = 20·103 Ом.
Сх -?
tgδ -?
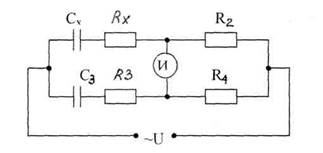
Рис. 4.1. Схема к задаче 4.07
Решение:
Для измерения емкости конденсаторов с малыми потерями показана на Рис. 4.1.
Для анализа используем эквивалентную схему Рис. 4.2.
Полные сопротивления плеч в данном случае:
Z1 = Rx + 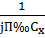 ;
;
Z2 = R2;
Z3 = R3 +  ;
;
Z4 = R4.
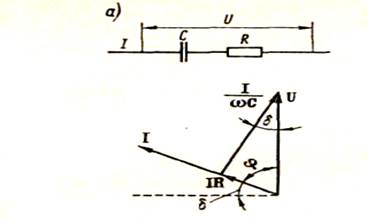
Рис. 4.2.Последовательная (а) эквивалентная схема и векторная диаграмма конденсатора с потерями
Подставив эти выражения в формулу равновесия моста, будем иметь

Отсюда получим условие равновесия моста:
Сx = C3 ·R4 / R2;
Rx = R3 ·R2 / R4.
Сx = 2000·10-12 ·20·103 / 40·103 = 1000·10-12 (Ф);
Rx = 40·103 ·40·103 / 20·103 = 80·103 (Ом) = 80 кОм.
Угол потерь δ, дополняющий до 90º угол фазового сдвига тока относительнго напряжения, определяется из выражения
tgδ = ω· Сx · Rx = ω· С3 · R3;
ω = 2πf;
tgδ = 2· 3,14·700·1000·10-12 ·80·103 = 351680000· 10-9 = 0,35168,
откуда
δ = 19º21`.
Задача 6.07
Для измерения сопротивления Rx используют амперметр с внутренним сопротивлением RA и вольтметр с внутренним сопротивлением Rv. При составлении схемы измерений вольтметр включается до амперметра и измеряет падение напряжения на амперметре и измеряемом сопротивлении или после амперметра (рис. 5). Определить, какая из двух схем дает меньшую погрешность измерения. Исходные данные для расчета приведены ниже.
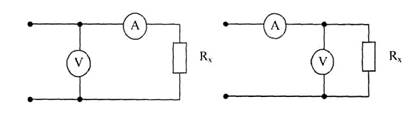
а) б)
Рис. 5. Схемы к задаче 6.07
Rx = 25 Ом;
RA = 5 Ом;
Rv = 15 кОм = 15·103 Ом.
Решение:
Измерение токов и напряжений всегда сопровождаются погрешностью, обусловленной сопротивлением используемого средства измерений. Включение в исследуемую цепь средства измерений искажает режим этой этой цепи. Включение амперметра, имеющего сопротивление RA в цепь, изображенную на Рис. 5,а, приведет к тому, что вместо тока I= U/R, который протекал в этой цепи до включения амперметра, после включения амперметра пойдет ток I1= U/(Rх+ RA).
Погрешность Δ I= I1- I = U/(Rх+ RA) - U/Rх
Для наглядного представления, примем U= 10 В.
Тогда I= 0,4 А;
I1= 0,3333 А;
Δ I= 0,0666 А и чем выше U, тем больше погрешность.
Показания же вольтметра почти не изменилось, т.к. RA меньше Rх.
По схеме, представленной на Рис. 5,б, при включении вольтметра параллельно резистору Rх, имеющего сопротивление Rv, для измерения напряжения на резисторе Rх, режим цепи тоже нарушается, т.к. вместо напряжения Uv = U· Rх / (Rх + RA), которое было в схеме до включения вольтметра, после его включения напряжение
Uv1 =  = 8,3313 (В).
= 8,3313 (В).
Uv = 8,333 В.
Тогда, погрешность ΔU = Uv - Uv1 = 0,0017 (В).
Поэтому можно сделать вывод:
1) Погрешность для Рис. 5,а тем выше, чем выше сопротивление амперметра;
2) Погрешность для Рис.5,б тем выше, чем меньше сопоротивление вольтметра
- поэтому первая схема дает меньшую погрешность измерения.
Выводы
При изучении получены знания по использованию методов и средств измерений, ознакомились с принципами работы и устройством основных измерительных приборов и систем, приобрели навыки проведения измерений.
ЛИТЕРАТУРА
1. Основы метрологии и электрические измерения. /Под ред. Е.М. Душина/ - Л. «Энергоатомиздат», 1987 – 480с.
2. Метрология, стандартизация и измерения в технике связи. /Под ред. Б.П. Хромого/. – М «Радио и связь», 1986 – 424с.
3. Кукуш В.Д. Электрорадиоизмерения – М. «Радио и связь», 1985 – 368с.
4. Винокуров В.И., Каплин С.И., Петелин И.Г. Электрорадиоизмерения – М, «Высшая школа»,1986 –351с.
5. Методические указания к изучению курса «Основы метрологии и измерительной техники» / Сост. Ф.Я. Шухат – Северодонецк; Изд-во СТИ, Восточноукр. Нац. Ун-та, 2000, 27 с.
6. Васильев А.С. Основы метрологии и технические измерения- М., Машиностроение, 1988 – 240 с.
7. Основы метрологии и электрические измерения: Учебник / Под ред. Е.М.Душина – Л., Энергоатомиздат, 1987 – 480 с.
8. Цюцюра С.В., Цюцюра В.Д. Метрологія, основи вимірювань, стандартизація та сертифікація: Навч. посіб. – К., Знання, 2005 – 242с.
ПРИЛОЖЕНИЕ
Таблица П.1
Значение нормированной функции Лапласа Ф(Z) 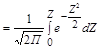
| Z | Ф(Z) | Z | Ф(Z) |
| 0,0 | 0,00000 | 2,1 | 0,48214 |
| 0,1 | 0,03983 | 2,2 | 0,48610 |
| 0,2 | 0,07926 | 2,3 | 0,48928 |
| 0,3 | 0,11791 | 2,4 | 0,49180 |
| 0,4 | 0,15542 | 2,5 | 0,49379 |
| 0,5 | 0,19146 | 2,6 | 0,49534 |
| 0,6 | 0,22575 | 2,7 | 0,49653 |
| 0,7 | 0,25804 | 2,8 | 0,49744 |
| 0,8 | 0,28814 | 2,9 | 0,48913 |
| 0,9 | 0,31594 | 3,0 | 0,49865 |
| 1,0 | 0,34134 | 3,1 | 0,49903 |
| 1,1 | 0,36433 | 3,2 | 0,49931 |
| 1,2 | 0,38493 | 3,3 | 0,49952 |
| 1,3 | 0,40320 | 3,4 | 0,49966 |
| 1,4 | 0,41924 | 3,5 | 0,49977 |
| 1,5 | 0,43319 | 3,6 | 0,49984 |
| 1,6 | 0,44520 | 3,7 | 0,49989 |
| 1,7 | 0,45543 | 3,8 | 0,49993 |
| 1,8 | 0,46407 | 3,9 | 0,49995 |
| 1,9 | 0,47128 | 4,0 | 0,499968 |
| 2,0 | 0,47725 | 4,5 | 0,499999 |