Работа, совершаемая идеальным газом при различных процессах.
Гироскоп.
Гироскопом ( или волчком) называется массивное
| Моменты инерции некоторых тел:
1. Тонкий стержень длины l
I=ml²/12
2. Брусок длиной а и шириной b
I=m(a²+b²)/12
3. Диск (цилиндр) радиусом R
I=mR²/2
4. Кольцо, внешний радиус которого R, а внутренний – r
I=m(R²+r²)/2
5. Тонкостенное кольцо (обруч)
I=m<R²>
6. Шар
I=2mR²/5
§3. Теорема Штейнера
Момент инерции I относительно произвольной оси равен сумме момента инерции IC относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:
I=IC+ma²
Рассмотрим ось С, проходящую через центр масс тела, и параллельную ей ось О, отстоящую от оси С на а. Обозначим Ri перпендикулярный к оси С вектор, проведенный от оси к элементарной массе Δmi, и R’i – аналогичный вектор от оси О. Между векторами имеется соотношение R’i=Ri+a.
| от расстояния точки ее приложения А до оси вращения, т.е. зависит от момента силы. Моментом М вращающей силы (вращающим моментом) называется произведение вращающей силы F на радиус окружности r, описываемой точкой приложения силы: M=Fr. (В общем случае моментом М силы F относительно точки О называется векторное произведение радиуса силы (расстояния между осью вращения и линией действия силы) r на вектор силы F: М=r×F. Численное значение момента силы может быть рассчитано по формуле M= rFsinα).
Другой характеристикой является момент инерции. Моментом инерции твердого тела называется сумма моментов инерции материальных точек этого тела относительно оси вращения, причем под моментом инерции материальной точки следует понимать произведение его массы на квадрат расстояния от оси вращения: I=mr².
§2. Основной закон вращательного движения.
Разобьем все тело на элементарные массы. Хотя сила F приложена к одной точке А тела, ее вращающее действие передается всем частицам: к каждой элементарной массе Δmi будет приложена элементарная вращающая сила ΔFi.
ΔFi=Δmiai
ΔFiri=Δmir²β
ΔMi=ΔIβ
Основной закон динамики вращения (второй закон Ньютона для вращательного движения): если на твердое
|
Сложение двух одинаково направленных колебаний одинаковой амплитуды, частоты которых мало отличаются друг от друга (биения).
Пусть тело одновременно участвует в двух одинаково направленных колебаниях с одинаковыми амплитудами А, но с различными круговыми частотами ω, мало отличающимися друг от друга.
В этом случае разность фаз колебаний оказывается переменной. Поэтому можно написать уравнения слагаемых колебаний без начальных фаз:
х1=А1sin(ω1t); х2=А2sin(ω2t)
х=х1+х2
Результирующее колебание оказывается негармоническим. Однако, учитывая, что
(ω1-ω2)/2<<(ω1+ω2)/2
можно считать результирующее колебание почти гармоническим, имеющим круговую частоту ω=(ω1+ω2)/2, период Т=2π/ω=4π/(ω1+ω2) и амплитуду 2Аcos[(ω1-ω2)/2]t, которая очень медленно периодически изменяется со временем. Такого рода колебания называются биениями (рис).
Сложение взаимно перпендикулярных гармонических колебаний
Пусть тело одновременно участвует в двух взаимно перпендикулярных колебаниях одинаковой частоты,
| свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания. На этом свойстве основано определение ускорения свободного падения с помощью оборотного маятника.
§5. Векторная диаграмма.
Решение ряда вопросов, в частности сложение нескольких колебаний одинакового направления (сложение нескольких функций), значительно облегчается и становится наглядным, если изображать колебания графически в виде векторов на плоскости. Полученная таким способом схема называется векторной диаграммой.
Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью х угол, равный начальной фазе колебаний.
§6. Сложение колебаний.
Сложение двух одинаково направленных гармонических колебаний одинаковой частоты.
Пусть тело одновременно участвует в двух одинаково направленных колебаниях одинаковой частоты, описываемых уравнениями
х1=А1sin(ω0t+α1); х2=А2sin(ω0t+α2)
Амплитуды и начальные фазы этих колебаний различны. Требуется определить характеристики результирующего колебания. Очевидно, что его смещение х равно алгебраической сумме смещений слагаемых
| точки или оси.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.
Отклонение маятника от положения равновесия – угол φ, образованный нитью с вертикалью. При отклонении маятника от положения равновесия возникает вращающий момент М, стремящийся вернуть маятник в положение равновесия (аналогичен квазиупругой силе). Следовательно: M=-mglsinφ
Подставим в уравнение динамики вращательного движения, обозначив угловое ускорение φ’’, а момент инерции равным ml²: mlφ’’=-mglsinφ.
φ’’+g/l sinφ=0
Примем g/l= ω0², и при малых углах sinφ≈φ:
φ’’+ω0²φ=0
Соответственно решение: φ=аcos(ω0t+α)
Частота колебаний математического маятника зависит только от длины маятника и от ускорения свободного падения и не зависит от массы маятника.
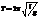Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. При отклонении маятника от положения равновесия на угол φ возникает вращающий момент, стремящийся вернуть
| Период колебания Т – время, за которое происходит одно полное колебание (фаза колебаний получает приращение 2π).
Т=2π/ω0
Число колебаний в единицу времени называется частотой колебаний ν.
ν=1/T
Соответственно: ω0=2π/Т
Это величина, равная числу колебаний за 2π секунд и называемая круговой или циклической частотой.
Продифференцируем уравнение колебаний, получив выражения для скорости и ускорения:
v=x’=-aω0sin(ω0+α)=aω0cos(ω0+α+π/2)
а =х’’=-aω02cos(ω0t+α)=αω0²cos(ω0t+α+π)
Выводы:
1. Как и смещение х, скорость v и ускорение а некоторой точки совершают гармонические колебания с одинаковой круговой частотой ω и периодом Т=2π/2.
2. Амплитуды этих колебаний различны: а – у смещения, ωа – у скорости и ω²а – у ускорения
3. Фазы колебаний также различны: колебание скорости опережает колебание смещения по фазе на π/2 (по времени на Т/4), колебание ускорения опережает колебание смещения по фазе на π (по времени на Т/2)
§3. Энергия гармонических колебаний.
Квазиупругая сила является консервативной. Поэтому полная энергия гармонического колебания
| mg=kΔl0 (Δl0 – удлинение пружины). Будем характеризовать смещение шарика из положения равновесия координатой х, причем ось х направим по вертикали вниз, а нуль оси совместим с положением равновесия шарика. Если сместить шарик в положение, характеризуемое координатой х, то удлинение пружины станет Δl0+х и проекция результирующей силы на ось х F=mg-k(Δl0+х). Получаем Fx=-kx. Т.о. результирующая сила тяжести и упругой силы имеет характер квазиупругой силы.
Сообщим шарику смещение х=а, после чего предоставим систему самой себе. Под действием квазиупругой силы шарик будет двигаться к положению равновесия со все возрастающей скоростью v=х’. При этом потенциальная энергия системы будет убывать, но зато появится все возрастающая кинетическая энергия. Придя в положение равновесия шарик продолжает двигаться по инерции. Это движение будет замедленным и прекратится тогда, когда кинетическая энергия полностью превратится в потенциальную, т.е. когда смещение шарика станет равным –а. Затем такой же процесс будет протекать при движении шарика в обратном направлении. Если трение в системе отсутствует, энергия системы должна сохранятся и шарик будет двигаться в пределах от х=а до х=-а неограниченно долго.
Уравнение второго закона Ньютона имеет вид:
mx’’=-kx
|
описываемых уравнениями
х=А1sin(ω0t+α1); у=А2sin(ω0t+α2)
где х – смещение, совершаемое по горизонтали, у – смещение по вертикали. Требуется определить характер результирующего движения тела.
х/А1=sinω0t∙cosα1+cosω0t∙sinα1
у/A2= sinω0t∙cosα2+cosω0t∙sinα2
Умножая первое уравнение на sinα2, а второе на sinα1и вычитая из первого второе (а затем умножив наоборот):
(x/A1)sinα2-(y/A2)sinα1=sinω0t∙sin(α2-α1)
(x/A1)cosα2-(y/A2)cosα1=-cosω0t∙sin(α2-α1)
Возведя их в квадрат и сложив, получаем уравнение траектории:
х²/А²1+у/A²2-2хуcos(α2-α1)/(A1A2)= sin²(α2-α1)
Рассмотрим два частных случая:
1. Амплитуды колебаний различны, начальные фазы одинаковы (A1≠A2, α1=α2). Тогда получим:
у=А2х/А1
Это уравнение прямой. Следовательно, результирующее колебание совершается вдоль прямой, проходящей через положение равновесия под углом α к направлению первого колебания:
tgα= А2/А1
Результирующее смещение:
| Применив обозначения: 2β=r/m, ω0²=k/m
x’’+2βx’+βω0²x=0
ω0 представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивление среды (при r=0). Эту частоту называют собственной частотой системы.
Общее решение уравнения:
здесь а0 и α – произвольные постоянные, ω – величина, определяемая формулой
В соответствии с видом функции движение системы можно рассматривать как гармоническое колебание частоты ω с амплитудой, изменяющейся по закону 
Скорость затухания колебаний определяется величиной β=r/2m, которую называют коэффициентом затухания. Время τ, за которое амплитуда уменьшается в е раз τ=1/β. Следовательно коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшается в е раз.
Период затухающих колебаний равен
| называемая добротностью колебательной системы. Добротность пропорциональна числу колебаний, совершаемых системой за то время, за которое амплитуда уменьшается в е раз.
§2. Автоколебания
При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды. Если восполнять эту убыль энергии, колебания станут незатухающими. Пополнение энергии системы может осуществляться за счет толчков извне, однако эти толчки должны сообщаться системе в такт с ее колебаниями, в противном случае они могут ослабить колебания и даже прекратить их совсем. Можно сделать так, чтобы колеблющаяся система сама управляла внешним воздействием, обеспечивая согласованность сообщаемых ей толчков со своим движением. Такая система называется автоколебательной, а совершаемые ею незатухающие колебания – автоколебаниями.
Пример автоколебательной системы – часовой механизм. Маятник часов насажен на одну ось с изогнутым рычагом – анкером. На концах анкера имеются выступы специальной формы, называемые палеттами. Зубчатое ходовое колесо находится под воздействием цепочки с гирей или закрученной пружины, которые стремятся повернуть его по часовой стрелке. Однако большую часть времени колесо упирается одним из зубьев в боковую поверхность той либо иной палетты, скользящей при
| Т.о. вторая функция описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. 
Для данной колебательной системы амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания φ также зависит от частоты вынуждающей силы.
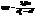§4. Резонанс.
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это называется резонансом, а соответствующая частота – резонансной частотой.
Чтобы определить резонансную частоту ωрез, нужно найти максимум функции
| среднем положении, то маятник сильно раскачается.
Увеличение энергии маятника при этом происходит за счет работы, которую совершает сила, действующая на нить. Сила натяжения нити при колебаниях маятника не постоянна: она меньше в крайних положениях, когда скорость обращается в нуль, и больше в среднем положении, когда скорость маятника максимальна. Поэтому отрицательная работа внешней силы при удлинении маятника оказывается меньше по величине, чем положительная работа, совершаемая при укорочении маятника. В итоге работа внешней силы за период оказывается больше нуля.
Волновое движение.
§1. Упругие волны.
Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространятся в среде от частицы к частице с некоторой скоростью v. Процесс распространения колебаний в пространстве называется волной.
Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором
|
| положения равновесия частиц, колеблющихся в одинаковой фазе). Волновой фронт все время перемещается. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической – множество концентрических сфер.
Расстояние λ, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Очевидно:
λ=vT
Длину волны можно определить как расстояние между ближайшими точками среды, колеблющимися с разностью фаз, равной 2π.
§2. Уравнения плоской и сферической волн.
Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x, y, z и времени t: ξ=ξ(x,y,z,t) Эта функция должна быть периодической как относительно времени, так и относительно координат. Периодичность по времени вытекает из того, что ξ описывает колебания частицы с координатами x, y, z. Периодичность по координатам следует из того, что точки, отстоящие друг от друга на расстояние λ, колеблются одинаковым образом.
| скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.
Волна, распространяющаяся в противоположном направлении описывается уравнением:
Уравнению плоской волны можно придать симметричный относительно х и t вид. Для этого введем величину
которая называется волновым числом.
При распространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается – наблюдается затухание волны. В однородной среде такое затухание происходит по экспоненциальному закону.
Уравнение сферической волны. Если ограничится рассмотрением волны на расстояниях от источника, значительно превышающих его размеры, то источник можно считать точечным. В изотропной и однородной среде волна, порождаемая таким источником, будет сферической.
| §4. Энергия упругой волны.
Пусть в некоторой среде распространяется в направлении оси х плоская продольная волна
Выделим в среде элементарный объем ΔV, чтобы скорость движения и деформацию во всех точках объема можно было считать одинаковыми и равными, соответственно, ∂ξ/∂t и ∂ξ/∂x. Тогда выражения для кинетической, потенциальной (как упругой деформации) и полной энергий:
Разделив энергию на объем, в котором она содержится, получим плотность энергии
Плотность энергии каждый момент времени в разных точках пространства различна. В одной и той же точке плотность энергии изменяется со временем по закону квадрата синуса. Среднее значение квадрата синуса равно
| время Δt энергия ΔW. Тогда плотность потока энергии:
т.к. ΔW=wΔS┴vΔt, v – фазовая скорость. Вектор j плотности потока энергии называется вектором Умова. Он различен в разных точках пространства, а в данной точке изменяется со временем по закону квадрата синуса. Его среднее значение равно
Когда говорят об интенсивности волны в данной точке, то имеют в виду среднее по времени значение плотности потока энергии, переносимой волной.
§5. Стоячие волны.
Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказывается геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это вытекающее из опыта утверждение называется принципом суперпозиции (наложения) волн.
Когда колебания, обусловленные отдельными волнами в каждой из точек среды, обладают постоянной разностью фаз, волны называются когерентными. При сложении когерентных волн возникает явление
| плоскость, точки которой имеют данное значение координаты.
В точках, координаты которых удовлетворяют условию 
амплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Это также не точки, а плоскости.
Расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно λ/2. Пучности и узлы сдвинуты друг относительно друга на четверть волны.
Основы молекулярной физики и физической кинетики.
Молекулярно-кинетическая теория.
Молекулярная физика – раздел физики, изучающий строение и свойства вещества исходя из так называемых молекулярно-кинетических представлений.
§1. Основные положения молекулярно-кинетической теории.
1. Все вещества состоят из очень маленьких отдельных частиц – молекул. Молекулы состоят из атомов. Размеры (диаметры) атомов имеют порядок 10-8-10-7 см. Самые крупные молекулы возможно рассмотреть под электронным микроскопом.
|
| потенциальной энергии взаимодействия молекул имеет минимум при r=r0. Следовательно, положение устойчивого равновесия молекул соответствует минимуму их потенциальной энергии. График зависимости потенциальной энергии от расстояния между молекулами – потенциальная кривая, АВС – потенциальная яма, В – дно потенциальной ямы, DВ – глубина потенциальной ямы.
Доказательство – сжимаемость газа, упругие деформации тел; невозможность восстановить разломанное тело путем простого составления его частей (из-за шероховатостей) указывает на то, что силы сцепления действуют на очень малых расстояниях.
3. Молекулы, образующие тело, находятся в состоянии непрерывного беспорядочного движения. Доказательством существования хаотического движения молекул служит броуновское движение – весьма малые взвешенные в жидкости частицы всегда находятся в состоянии непрерывного беспорядочного движения, которое не зависит от внешних причин и оказывается проявлением внутреннего движения вещества. Броуновские частицы совершают движение под влиянием беспорядочных ударов молекул.
Другое доказательство – явление диффузии (проникновение молекул одного вещества между молекулами другого).
4. Его интенсивность (средняя скорость частиц)
| микроскопическую природу тел. В основе термодинамики лежат фундаментальные законы (начала термодинамики), установленные путем обобщения очень большого числа опытных фактов на основе законов превращения энергии.
§3. Масса молекул.
Относительной атомной массой (Ar) химического элемента называется отношение массы атома этого элемента к 1/12 массы атома 12С. Относительной молекулярной массой (Мr) вещества называется отношение массы молекулы этого вещества к 1/12 массы атома 12С. Эти величины безразмерны.
Масса, равная 1/12 массы атома 12С, называется атомной единицей массы (а.е.м.).
Моль представляет собой количество вещества, в котором содержится число частиц, равное числу атомов в 12г 12С.
Число частиц, содержащихся в моле вещества, называется постоянной Авогадро. Опытным путем установлено, что она равна NA=6,02213∙1023 моль-1.
Масса моля М – молярная масса. Она равна произведению постоянной Авогадро на массу молекулы:
M=NAMrmед
Отсюда можно найти mед, она равна 1,66∙10-27кг.
Масса атома равна произведению относительной атомной массы на а.е.м.
| первоначальное отклонение какой-либо величины от равновесного значения уменьшается в е раз, называется временем релаксации. Для каждого параметра состояния имеется свое время релаксации. Наибольшее из этих времен представляет собой время релаксации системы.
Термодинамическим процессом называется переход системы из одного состояния в другое. Такой переход всегда связан с нарушением равновесия системы. Бесконечно медленный процесс состоит из последовательности равновесных состояний. Такой процесс называется равновесным или квазистатическим. Бесконечно медленный процесс является абстракцией. Практически можно считать квазистатическим процесс, протекающий настолько медленно, что отклонения значений параметров от равновесных пренебрежимо малы.
При изменении направления равновесного процесса система будет проходить через те же равновесные состояния, что и при прямом ходе, но в обратной последовательности. Поэтому равновесные процессы называют также обратимыми.
Процесс, при котором система после ряда изменений возвращается в исходное состояние, называется круговым процессом или циклом.
Все количественные выводы термодинамики применимы только к равновесным состояниям и обратимым процессам.
| разности значений внутренней энергии в конечном и начальном состояниях.
§6. Теплота и температура.
Тепловое состояние тела (вещества) определяется интенсивностью хаотического (теплового) движения его молекул. При изменении интенсивности этого движения изменяются внутренняя энергия тела и его тепловое состояние.
Температура – скалярная величина, характеризующая тепловое состояние тела, количественно описывающая интенсивность хаотического движения его молекул. Чем интенсивнее тепловое движение молекул в теле, тем выше его температура. Если при тепловом контакте тепловые состояния тел не изменяются, то их температура одинакова – тела находятся в тепловом равновесии.
Простейшим и наиболее распространенным термометром является жидкостный (ртутный или спиртовой), в качестве температурного признака которого выбрано свойство тел (жидкости) расширятся при нагревании. В шкале Цельсия выбраны две точки столбика уровня жидкости: таяние льда и кипение воды, между которыми сто делений, каждое из которых 1ºС.
В физике пользуются термодинамической температурой, которая имеет глубокий физический смысл (термодинамическая температура определяется средней кинетической энергией, приходящейся на одну молекулу
| Обозначения: А – работа, совершаемая данным телом над внешними телами, А’ – работа, совершаемая внешними телами над телом, Q – количество теплоты, переданное данному телу внешней средой, Q’ – количество теплоты, переданное данным телом внешней средой.
При совершении одним телом работы А над другим, равно как и при сообщении одним телом другому теплоты Q, эти тела обмениваются внутренней энергией – энергия одного тела увеличивается, другого на столько же уменьшается.
Q=U2-U1+A
Количество теплоты, сообщенное системе, идет на приращение внутренней энергии системы и на совершение системой работы над внешними телами.
Совершенная системой работа и количество полученной системой теплоты зависят от пути перехода системы из одного состояния в другое. Следовательно, ни Q, ни А не являются функциями состояния, в силу чего нельзя говорить о запасе теплоты или работы, которым обладает система в различных состояниях.
§8. Работа, совершаемая телом при изменениях объема.
Взаимодействие данного тела с соприкасающимися с ним телами можно охарактеризовать давлением, которое оно оказывает. Перемещение точек приложения сил взаимодействия сопровождается изменением объема тела. Следовательно, работа, совершаемая данным телом над
|
| распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением к сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.
Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.
Геометрическое место точек, колеблющееся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновые поверхности остаются неподвижными (они проходят через
|
или, что тоже самое, минимум выражения, стоящего под корнем в знаменателе. Продиффернцировав это выражение по ω и приравняв нулю, получаем условие определяющее ωрез:
Уравнение имеет три решения: при нуле – максимум знаменателя, отрицательное не имеет смысла. Т.о. 
Подставив его в уравнение амплитуды, получим выражение для амплитуды при резонансе:
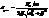§5. Параметрический резонанс.
Существует иной вид воздействия, с помощью которого можно раскачать систему. Этот вид воздействия заключается в совершаемом в такт с колебаниями периодическом изменении какого-либо параметра системы, вследствие чего само явление называется параметрическим резонансом.
Пример: простейший маятник – шарик на нити. Если периодически изменять длину маятника l, увеличивая ее в моменты, когда маятник находится в крайних положениях, и уменьшая в моменты, когда маятник находится в
| качании маятника по поверхности зуба. Только в моменты, когда маятник находится вблизи среднего положения, палетты перестают преграждать путь зубьям и ходовое колесо проворачивается, толкая анкер зубом, скользящим своей вершиной по скошенному торцу палетты. За полный цикл качаний маятника (за период) ходовое колесо проворачивается на два зуба, причем каждая из палетт получает по толчку.
§3. Вынужденные колебания.
Пусть колебательная система подвергается действию внешней силы, изменяющейся со временем по гармоническому закону:
Fx=F0cos ωt
В этом случае уравнение второго закона Ньютона:
mx’’=-kx-rx’+F0cosωt
x’’+2βx’+βω0²x=f0cosωt
где 2β=r/m, ω0²=k/m, f0=F0/m
Общее решение этого уравнения:
Первое слагаемое играет заметную роль только в начальной стадии процесса, при так называемом установлении колебаний. С течением времени из-за множителя exp(-βt) роль этого слагаемого уменьшается, и по прошествии достаточного времени им можно пренебречь, сохраняя в решении лишь второе слагаемое.
| При незначительном сопротивлении среды (β²<<ω0²) период колебаний практически равен Т0=2π/ω0. С ростом коэффициента затухания период колебаний увеличивается.
Последующие амплитуды отклонения образуют геометрическую прогрессию.
Отношение значений амплитуд, соответствующих моментам времени, различающимися на период, равно
Это отношение называют декрементом затухания, а его логарифм – логарифмическим декрементом затухания:
Отсюда: 
За время τ, за которое амплитуда уменьшается в е раз, система успевает совершить N e =τ/T. Отсюда, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то же время, за которое амплитуда уменьшается в е раз.
Для характеристики колебательной системы часто употребляется также величина
Q=π/λ=πN e
| 2. Амплитуды колебаний различны, начальные фазы отличаются на π/2 (A1≠A2, α1-α2=π/2). Тогда:
х2/А12+у2/А22=1
Это уравнение эллипса. Результирующее движение тела совершается по эллипсу, полуоси которого равны амплитудам слагаемых колебаний. (рис)
х=А1sin(ω0t+α1); у=А2sin(ω0t+α1+π/2)
Затухающие и вынужденные колебания.
§1. Затухающие колебания
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем наиболее часто встречающемся, случае сила сопротивления F* пропорциональна скорости:
F*x=-rx’
Здесь r – постоянная, называемая коэффициентом сопротивления.
Знак минус обусловлен тем, что сила F* и скорость v имеют противоположные направления; следовательно, их проекции на ось х имеют разные знаки.
Уравнения второго закона Ньютона при наличии сил сопротивления имеет вид
mx’’=-kx-rx’
|
| 2. Между молекулами тела одновременно действуют силы взаимного притяжения (сцепления) и силы взаимного отталкивания. При этом силы отталкивания должны убывать с увеличением расстояния быстрее, чем силы сцепления. Только при этом условии молекулы могут находится в устойчивом равновесии на некотором определенном расстоянии друг от друга (на котором силы отталкивания равны силам сцепления). Если под влиянием каких-либо причин молекулы сблизятся на расстояние меньшее (большее) равновесного, то силы отталкивания (сцепления) начнут преобладать и восстановят равновесное состояние между молекулами.
Согласно экспериментальным и теоретическим исследованиям f обратно пропорциональны n-ой степени расстояния r между молекулами. Для сил притяжения n=7, для сил отталкивания n=9÷15. (граф.)
Характер зависимости потенциальной энергии W взаимодействия молекул от расстояния между ними. При r=∞ W=0. Если молекулы окажутся на расстоянии r≈1,5∙10-7 см друг от друга, то они начнут сближаться за счет работы сил притяжения, а потенциальная энергия молекул будет при этом уменьшаться и достигнет минимального значения при r=r0 (при F=0). Дальнейшее сближение молекул возможно только за счет работы, совершаемой против сил отталкивания. При этом потенциальная энергия молекул начнет резко возрастать. В результате кривая
| интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга.
Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну.
Упростив: 
В точках, координаты которых удовлетворяют условию: 
амплитуда колебаний достигает максимального значения. Эти точки называются пучностями стоячей волны. Координаты пучностей: хпучн=±nλ/2. Пучность представляет собой не одну единственную точку, а
| половине. Соответственно среднее по времени значение плотности энергии в каждой точке среды равно
Среда, в которой распространяется волна, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной; следовательно волна переносит с собой энергию. Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Поток энергии равен:
Поток энергии скалярная величина, размерность совпадает с размерностью мощности.
Поток энергии в разных точках среды может обладать различной интенсивностью. Для характеристики течения энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии. Эта величина численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.
Пусть через площадку ΔS┴, перпендикулярной направлению распространения волны, переносится за
| 
а – амплитуда на расстоянии от источника, равном единице; r – радиус поверхности. Для поглощающей среды в формулу добавляется множитель экспоненты.
§3. Волновое уравнение.
Уравн
|
Поиск по сайту:
|