Тема 4. Показатели вариации
Понятие вариации. Задачи статистического изучения вариации.
Повторим некоторые определения, изученные ранее
| Понятие | Определение |
| Вариация | _______________________________________________ |
Варианты
| ______________________________________________________ ______________________________________________________ ______________________________________________________ |
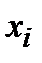
Частоты (повторения)
| ______________________________________________________ ______________________________________________________ |
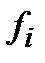
Частость
| ______________________________________________________ ______________________________________________________ ______________________________________________________ ______________________________________________________ |
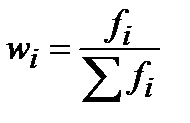
| Вариационный ряд | ______________________________________________________ ______________________________________________________ ______________________________________________________ ______________________________________________________ |
О факторах ____________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задачи статистического изучения вариации:
1) ______________________________________________________________________
____________________________________________________________________________
2) ______________________________________________________________________
____________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
Для измерения вариации признака применяются различные
абсолютные и относительные показатели.
| Показатели вариации |
| Абсолютные показатели |
| коэффициент осцилляции |
| размах вариации |
| среднее линейное отклонение |
| дисперсия |
| среднее квадратическое отклонение |
| коэффициент вариации |
| относительное линейное отклонение |
| Относительные показатели |
Такие показатели вариации, как среднее линейное отклонение, дисперсия и среднее квадратическое отклонение основаны на рассмотрении отклонений значений признака отдельных единиц совокупности от средней арифметической.
Размах вариации
Размах вариации (R) _____________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
Среднее линейное отклонение
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
Среднее линейное отклонение ________________________________________________
________________________________________________________________________________
________________________________________________________________________________
| 
|
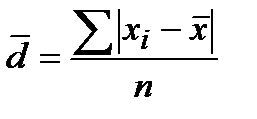
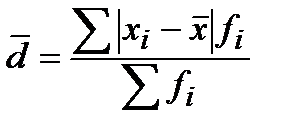
| простая форма - применяется, если каждая из вариант встречается в совокупности только один раз | взвешенная форма - применяется, если каждая из вариант встречается в совокупности несколько раз |
Здесь d - __________________________________________________________
- ________________________________________________________________________
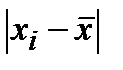f - _______________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
| Необходимость использования в формулах среднего линейного отклонения модулей отклонений вариант от средней вызвана тем, что алгебраическая сумма этих отклонений равна нулю по свойствам средней арифметической. |
Дисперсия. Свойства дисперсии. Дисперсия альтернативного признака
Дисперсия (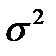
)– _________________________________________________________________
________________________________________________________________________________
В зависимости от исходных данных дисперсия вычисляется:
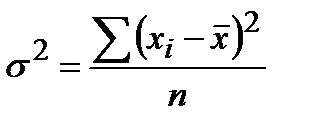– простая или 
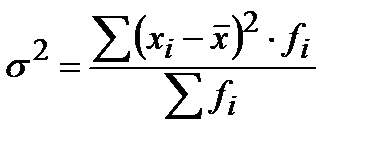– взвешенная.
Свойства дисперсии (повторить самостоятельно).
1. ______________________________________________________________________________
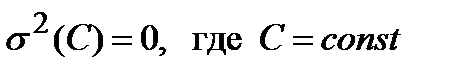
2. _________________________________________________________________________
________________________________________________________________________________
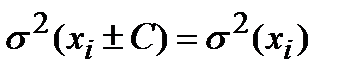
3. ____________________________________________________________________________
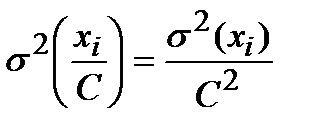и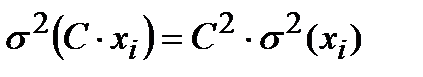 
Используя свойства среднего и дисперсии получим более простую формулу расчёта последней.
В соответствии с определением дисперсии:
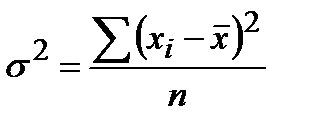
Теперь, раскроем скобки.
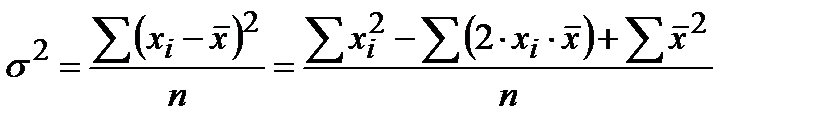
Т.к. средняя арифметическая для заданного набора данных является величиной постоянной, то для удвоенного произведения можно применить свойство 1 средней:
.
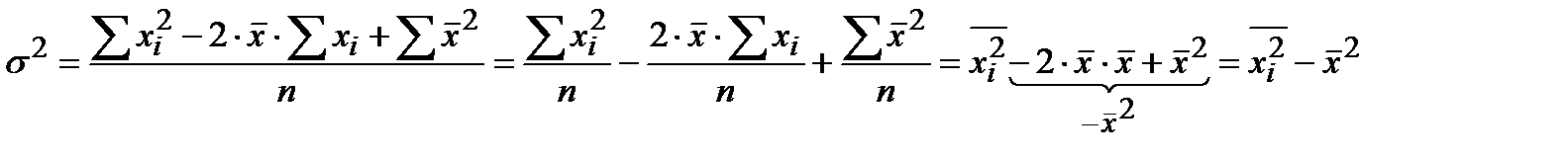Итак:
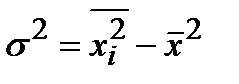
Дисперсия альтернативного признака
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
Средняя величина альтернативного признака: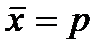 
Вывод формулы:
Дисперсия альтернативного признака: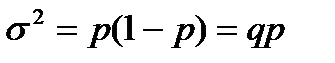 
Вывод формулы:
Виды дисперсии. Правило сложения дисперсии.
Различают три вида дисперсий
| Виды дисперсий |
| Общая дисперсия |
| Внутригрупповая дисперсия |
| Межгрупповая дисперсия |
| Простая |
| Взвешенная |
| Простая |
| Взвешенная |
| Простая |
| Взвешенная |
1. Общая дисперсия ________________________________________________________________
________________________________________________________________________________
Вычисляется по формулам:
| 
|
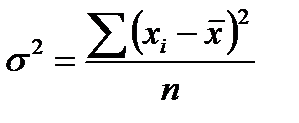
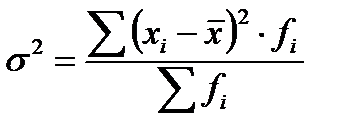
2. Внутригрупповая дисперсия (частная, остаточная, случайная) ________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
Вычисляется по формуле:
| 
|
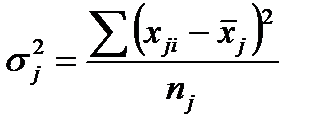
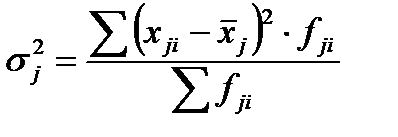
здесь j – номер группы, i – номер элемента в каждой j -й группе.
Пример.
Группа 1
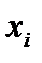
| -1 |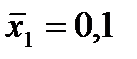 
| |||
|
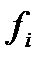
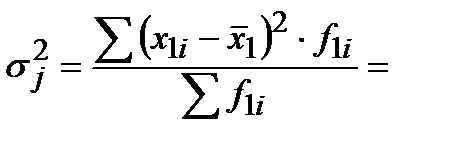
Группа 2
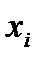
| - 1 |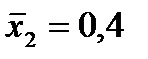 
| |||
|
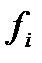
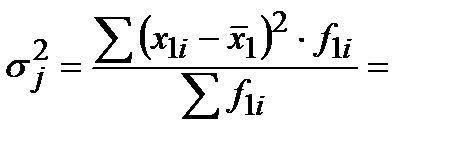
Средняя из внутригрупповых дисперсий ________________________________________________
________________________________________________________________________________
________________________________________________________________________________
|
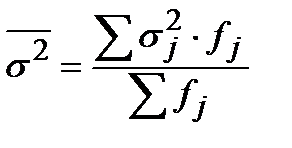
Она рассчитывается по формуле:
Для нашего примера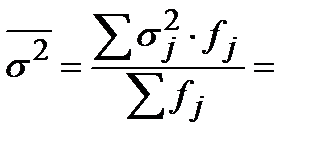 
3. Межгрупповая дисперсия (факторная) ___________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
|
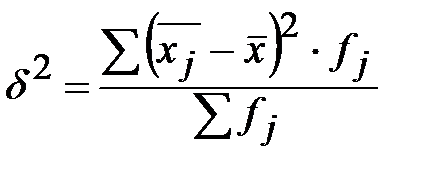
Правило сложения дисперсии в статистике
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
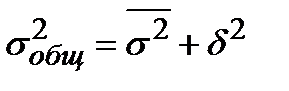
Среднее квадратическое (стандартное) отклонение.
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
Относительные показатели вариации (коэффициент вариации, коэффициент осцилляции, линейный коэффициент вариации, децильный коэффициент вариации)
В статистической практике часто возникает необходимость сравнения вариации различных признаков. При сравнении изменчивости различных признаков в совокупности, для оценки интенсивности вариации, для сравнения ее в разных совокупностях и для разных признаков удобно применять относительные показатели вариации. Эти показатели вычисляются как отношение абсолютных показателей к средней арифметической или медиане. Используя в качестве абсолютного показателя вариации размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, получают относительные показатели изменчивости.
| Коэффициент осцилляции (или относительный размах вариации) |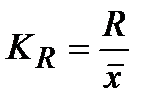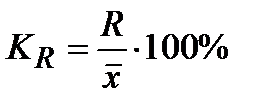  
| _________________________________________ _________________________________________ _________________________________________ _________________________________________ |
| Линейный коэффициент вариации (или относительное линейное отклонение) |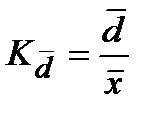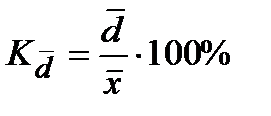  
| _________________________________________ _________________________________________ _________________________________________ _________________________________________ |
| Коэффициент вариации |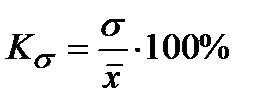  
| _________________________________________ _________________________________________ _________________________________________ _________________________________________ |
где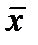 
– ________________________________
R – ________________________________
– ________________________________
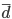σ – ________________________________
Замечание (об однородности совокупности). _________________________________________
________________________________________________________________________________
________________________________________________________________________________