Дана электрическая цепь и значение всех элементов. Требуется рассчитать комплексные токи во всех ветвях. Для этого выбираем произвольно направление всех комплексных токов в ветвях на исходной схеме. Представим схему в комплексном виде. Исходная схема представлена на рисунке 3.

Рис. 3
Выбираем произвольно положительные направления контурных токов во всех ветвях и рассчитываем необходимо количество уравнений по первому и второму законом Кирхгофа:
y=Ny-1=2-1=1
k=Nв-Nу+1-Nт =3-2+1-0=2
Запишем уравнение по первому закону Кирхгофа для первого узла:

|
Запишем два уравнения по второму закону Кирхгофа. Достаточным условием независимости может быть требование, что каждый новый замкнутый контур должен содержать хотя бы одну новую ветвь.

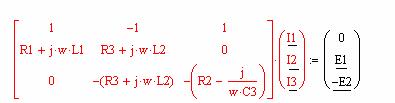
или
ZI=E
Далее находим токи.
I=Z-1E,
где:
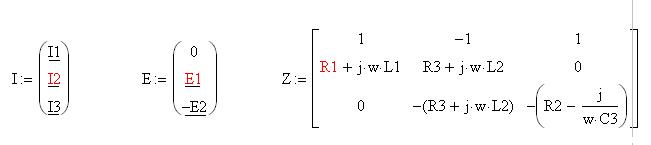
Для подсчета данного уравнения используем программу Mathcad 14, отсюда получаем результаты:

Построим векторную диаграмму (Рис 4):

Рис. 4
Метод контурных токов
Выбираем произвольно положительные направления комплексных токов и контурных токов. Исходная схема с учетом данного метода представлена на рис. 5.

Рис.5
Рассчитываем необходимое количество независимых контуров:
k=Nв-Nу+1-Nт =3-2+1-0=2
Обозначаем контурные токи Iii так, чтобы каждый из них проходил через один источник тока. Составляем следующую систему:

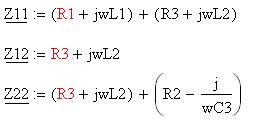
Таким образом, систему можно переписать в следующем виде:
ZI=E
Далее находим токи.
I=Z-1E,

Для подсчета данного уравнения используем программу Mathcad 14, отсюда получаем результаты:

То есть:

Теперь вычислим истинные комплексные токи во всех ветвях, используя первый закон Кирхгофа для комплексных величин как алгебраическую сумму контурных токов, протекающих по данной ветви.
Получим:


Метод узловых потенциалов
Исходная схема с учетом данного метода представлена на рисунке 6.

Рис. 6
Произвольно выбираем направления всех комплексных токов в ветвях на исходной схеме. Определить количество уравнений N системы уравнений:

Пусть потенциал узла 2 будет равен нулю(V2=0). Решим систему уравнений относительно потенциала узла 1.

Получаем:


Получаем:

Подставляем V 1 в обобщенный закон Ома, получаем значения искомых комплексных токов:



Метод двух узлов
Методом двух узлов для комплексных величин определяется комплексным напряжение между этими узлами, а затем по величине этого напряжения определяются комплексные токи ветвей. В нашей схеме примем, что I =0. Искомая схема представлена на рисунке 7.

Рис. 7
Искомая формула, по которой мы будем искать комплексное напряжение между двумя узлами имеет вид:




Метод наложения
Произвольно выбираем направление всех комплексных токов в ветвях и пронумеруем все независимые источники целыми числами. Исходная схема представлена на рисунке 8.

Рис. 8
Положить равным нулю все источники ЭДС и комплексного тока кроме первого. При этом независимые источники, ЭДС которых равна нулю, заменяем короткозамкнутыми отрезками. Исходная схема представлена на рисунке 9.

Рис. 9
Таким образом, получаем:


Положить равным нулю все источники ЭДС и комплексного тока кроме второго. При этом независимые источники, ЭДС которых равна нулю, заменяем короткозамкнутыми отрезками. Исходная схема представлена на рисунке 10.

Рис. 10


Подставляем все значения и получаем:
