ЛЕКЦИЯ 12
В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом причинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Самым распространенным в настоящее время формализмом, описывающим структуру и взаимодействие параллельных систем и процессов, являются сети Петри (англ. Petri Nets), предложенные К. Петри [8].
Основные соотношения. Теория сетей Петри развивается в нескольких направлениях: разработка математических основ, структурная теория сетей, различные приложения (параллельное программирование, дискретные динамические системы и т. д.).
Формально сеть Петри (N-схема) задается четверкой вида
N=<B, D, 1, О>,
где В - конечное множество символов, называемых позициями, B  Ø;D- конечное множество символов, называемых переходами, D≠Ø, B∩D≠Ø; I - входная функция (прямая функция инцидентности), O: D
Ø;D- конечное множество символов, называемых переходами, D≠Ø, B∩D≠Ø; I - входная функция (прямая функция инцидентности), O: D  B →{0,1}; О - выходная функция (обратная функция инцидентности), О: D× В→{О, 1}. Таким образом, входная функция 1 отображает переход dj в множество входных позиций b
B →{0,1}; О - выходная функция (обратная функция инцидентности), О: D× В→{О, 1}. Таким образом, входная функция 1 отображает переход dj в множество входных позиций b 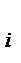
 I (d
I (d  ), а выходная функция О отображает переход dj в множество выходных позиций b
), а выходная функция О отображает переход dj в множество выходных позиций b 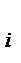
 D (d
D (d  ). Для каждого перехода dj
). Для каждого перехода dj  D можно определить множество входных позиций перехода I(dj) и выходных позиций перехода О (dj) как
D можно определить множество входных позиций перехода I(dj) и выходных позиций перехода О (dj) как
I (d  )={ b
)={ b 
 │ I (b
│ I (b  , d
, d  )=1} i=
)=1} i=  ; j=
; j=  , n =│ B │, m =│ D │
, n =│ B │, m =│ D │
O (d  )={ b
)={ b 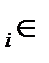 B │ O (d
B │ O (d  , b
, b  )=1}
)=1}
Аналогично, для каждого перехода b  В вводятся определения множества входных переходов позиции I(b
В вводятся определения множества входных переходов позиции I(b 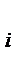 )и множества выходных переходов позиции
)и множества выходных переходов позиции
О (b j): I (b  )={d
)={d  D│I(d
D│I(d  ,b
,b  )= 1}, О (b
)= 1}, О (b  )={d
)={d  D │ О (b
D │ О (b  )= 1}.
)= 1}.
Графически N -схема изображается в виде двудольного ориентированного мультиграфа, представляющего собой совокупность позиций и переходов (рис. 6.1).
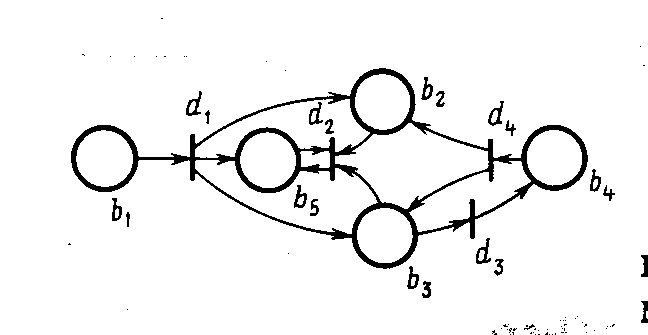
Рис. 6.1. Графическое изображение N-схемы
Как видно из этого рисунка, граф N -схемы имеет два типа узлов: позиции и переходы, изображаемые О и 1 соответственно. Ориентировочные дуги соединяют позиции и переходы, причем каждая дуга направлена от элемента одного множества (позиции, или перехода) к элементу другого множества (переходу или позиции). Граф N -схемы является мультиграфом, так как он допускает существование кратных дуг от одной вершины к другой.
Представим формально N-схему, показанную в виде графа на рис. 6.1
N =< B, D, I, О >,
В =< b  ,b
,b  ,b
,b  ,b
,b  ,b
,b 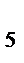 >,
>,
D=<d  ,d
,d  ,d
,d  ,d
,d  >,
>,
I (d  ) = { b
) = { b  }, О (d
}, О (d  )= { b2, Ьз, bs },
)= { b2, Ьз, bs },
I (d2) = { b  ,b
,b  ,b
,b  }, О (d2) = { bs },
}, О (d2) = { bs },
I (dз)= { ЬЗ }. О (dз) = { b  }.
}. 
I (d  ) = { b
) = { b  }, О (d
}, О (d  ) = { b
) = { b 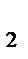 ,b
,b  }.
}.
Возможные приложения. Приведенное представление N-схемы может использоваться только для отражения статики моделируемой системы (взаимосвязи событий и условий), но не позволяет отразить в модели динамику функционирования моделируемой системы. Для представления динамических свойств объекта вводится функция маркировки (разметки) М: В→ {О, 1, 2,... }. Маркировка М есть присвоение неких абстрактных объектов, называемых метками (фишками), позициям N -схемы, причем количество меток, соответствующее каждой позиции, может меняться. При графическом задании N-схемы разметка отображается помещением внутри вершин-позиций соответствующего числа точек (когда количество точек велико, ставят цифры).
Маркированная (размеченная) N -схема может быть описана в виде пятерки N  = < B, D, I, O, M > и является совокупностью сети Петри и маркировки М [8].
= < B, D, I, O, M > и является совокупностью сети Петри и маркировки М [8].
Функционирование N -схемы отражается путем перехода от разметки к разметке. Начальная разметка обозначается как М  : В →{О, 1, 2,...}.
: В →{О, 1, 2,...}.
Смена разметок происходит в результате срабатывания одного из переходов d  D сети. Необходимым условием срабатывания перехода d
D сети. Необходимым условием срабатывания перехода d  является b
является b 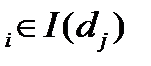 { М (b
{ М (b  ) ≥1}, где М (b
) ≥1}, где М (b  ) - разметка позиции b
) - разметка позиции b  . Переход d
. Переход d 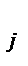 , для которого выполняется указанное условие, определяется как находящийся в состоянии готовности к срабатыванию или как возбужденный переход.
, для которого выполняется указанное условие, определяется как находящийся в состоянии готовности к срабатыванию или как возбужденный переход.
Срабатывание перехода d 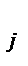 изменяет разметку сети М (b)на разметку М '(b) по следующему правилу:
изменяет разметку сети М (b)на разметку М '(b) по следующему правилу:
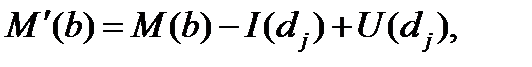
т. е. переход d  изымает по одной метке из каждой своей входной позиции и добавляет по одной метке в каждую из выходных позиций. Для изображения смены разметки М на М' применяют обозначение M └
изымает по одной метке из каждой своей входной позиции и добавляет по одной метке в каждую из выходных позиций. Для изображения смены разметки М на М' применяют обозначение M └  M'.
M'.
Рассмотрим размеченную N - схему с начальной разметкой М  = {1, О, О, О, 1, О, 1}, которая приведена на рис. 6.2, а. При такой начальной разметке N-схемы единственным готовым к срабатыванию является переход d2, срабатывание которого ведет к смене разметка МО └
= {1, О, О, О, 1, О, 1}, которая приведена на рис. 6.2, а. При такой начальной разметке N-схемы единственным готовым к срабатыванию является переход d2, срабатывание которого ведет к смене разметка МО └  M1, rдe М1 = {О, 1, 1, О, 1, О, 1} (рис. 6.2, б).
M1, rдe М1 = {О, 1, 1, О, 1, О, 1} (рис. 6.2, б).
При разметке М1 возможно срабатывание переходов d  ,d
,d  и d
и d  .В зависимости от того, какой переход сработал первым, получается одна из трех возможных новых маркировок (рис. 6.2, в, г, д). Функционирование N-схемы продолжается до тех пор, пока существует хотя бы один возможный переход.
.В зависимости от того, какой переход сработал первым, получается одна из трех возможных новых маркировок (рис. 6.2, в, г, д). Функционирование N-схемы продолжается до тех пор, пока существует хотя бы один возможный переход.

Рис. 6.2. Пример функционирования размеченной N-схемы.
Таким образом, N- сxeма выполняется путем запусков переходов под управлением количества меток и их распределения в сети. Переход запускается удалением меток из его входных позиций и образованием новых меток, помещаемых в выходные позиции. Переход может запускаться только тогда, когда он разрешен. Переход называется разрешенным, если каждая из его входных позиций имеет число меток, по крайней мере равное числу дуг из позиции в переход.
Важной особенностью моделей процесса функционирования систем с использованием типовых N -схем является простота построения иерархических конструкций модели. С одной стороны, каждая N -схема может рассматриваться как макропереход или макропозиция модели более высокого уровня. С другой стороны, переход или позиция N-схемы может детализироваться в форме отдельной подсети для более углубленного исследования процессов в моделируемой системе S. Отсюда вытекает возможность эффективного использования N-схем для моделирования параллельных и конкурирующих процессов в различных системах.