Решение типовых примеров

Решение типовых примеров

1 Проверить, является ли дифференцируемой функция а) 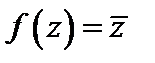; б) .

Решение. а) Функция 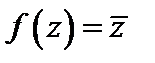непрерывна на всей комплексной плоскости . Она может быть представлена в виде . Тогда при любом имеем .

Приращение может стремиться к нулю по любому направлению. Выбирая для два различных направления, получим два различных значения отношения:

– если , , 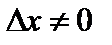то ;

– если , , то .

Следовательно, предел не существует. Функция непрерывная на всей комплексной плоскости не имеет производной ни в одной точке плоскости.

б) Пусть . Тогда 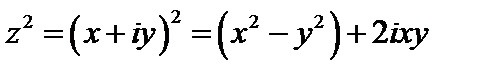. Следовательно, , 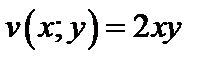. Условия Коши-Римана , выполняются в любой точке . Значит, функция дифференцируема на всей комплексной плоскости. Тогда

.

2 Найти аналитическую функцию , если при условии .

Решение. Частные производные первого и второго порядков функции равны:

, ; , .

Функция является гармонической на всей комплексной плоскости , так как

.

Согласно теореме 4, существует функция , сопряженная к . Проинтегрируем 1-е условие Коши-Римана по переменной :

.

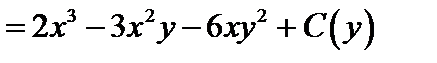Дифференцируя последнее равенство по переменной и подставляя во 2-е условие Коши-Римана , получим .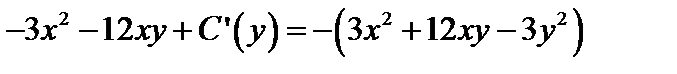

Отсюда . Интегрируя по , получим , .Тогда аналитическая функция имеет вид

.

Из условия находим постоянную : . Искомая функция примет вид

== .

3 Найти коэффициент растяжения и угол поворота при отображении 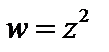в точке .

Решение. Имеем . Тогда

.

Так как , ,

то при отображении 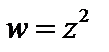происходит растяжение с коэффициентом, равным 4, и поворот против часовой стрелки на угол, равный .

ИЗ - 3 Интегрирование функции комплексной переменной

1 Вычислить интегралы (в интегралах по замкнутому контуру контур обходит против часовой стрелки).

1.1	а)	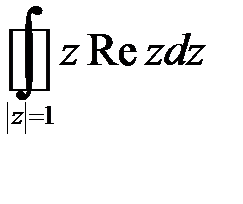б) .
1.2	а)	б) .
1.3	а)	б) .
1.4	а)	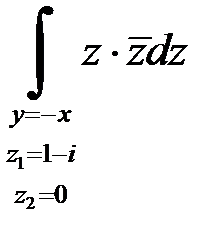б) .
1.5	а)	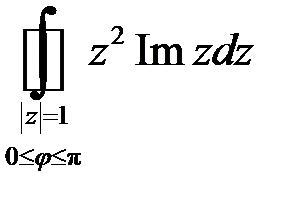б) .
1.6	а)	б) .
1.7	а)	б) .
1.8	а)	б)
1.9	а)	б) .
1.10	а)	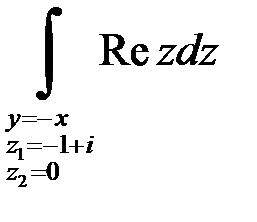б) .
1.11	а)	б) .
1.12	а)	б) .
1.13	а)	б) .
1.14	а)	б) .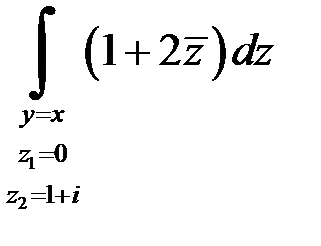

2 Вычислить интегралы по замкнутому контуру с помощью интегральной формулы Коши (контур обходится против часовой стрелки), сделать чертеж.

 

2.1	а)	б)	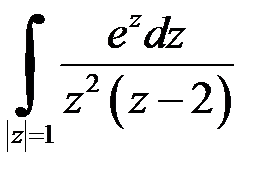в)
2.2	а)	б)	в)
2.3	а)	б)	в)
2.4	а)	б)	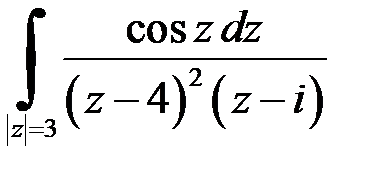в)
2.5	а)	б)	в)
2.6	а)	б)	в)
2.7	а)	б)	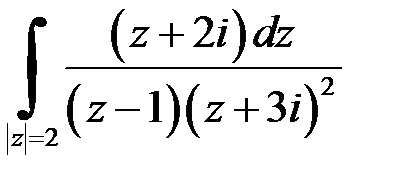в)
2.8	а)	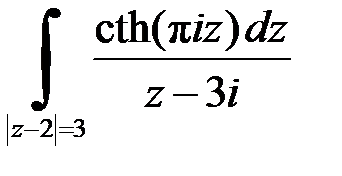б)	в)
2.9	а)	б)	в)
2.10	а)	б) .	в)
2.11	а)	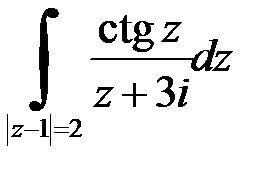б)	в)
2.12	а)	б)	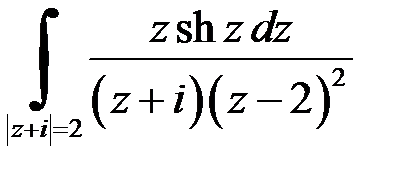в)
2.13	а)	б)	в)
2.14	а)	б)	в)
2.15	а)	б)	в)

Решение типовых примеров

 

1 Вычислить интегралы

а) ; б) 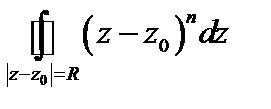при ; в) .

Решение. а) по формуле Ньютона-Лейбница имеем:

;

б) параметрические уравнения окружности с центром в точке имеют вид:

Отсюда комплексно-параметрическое уравнение окружности есть

, .

Тогда по теореме 1 получим:

;

в) имеем:

.

2 Вычислить , где – отрезок прямой , соединяющий точки и .

Решение. 1 способ. Так как контур интегрирования – прямая , сделаем замену . Тогда

, ,

где является постоянным и .

Таким образом,

, , ; .

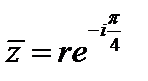В точке имеем , а в точке получим:

.

Тогда получим:

.

2 способ. Выделим действительную и мнимую части исходной функции:

.

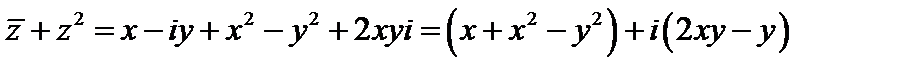Отсюда

;

.

Тогда получим

.

3 Вычислить , где – часть окружности , расположенная в верхней полуплоскости.

Решение. Положим . Так как , то и . Тогда и по условию.

Тогда по теореме 1 получим

.

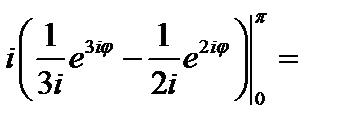
4 Вычислить , где 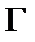– отрезок прямой , соединяющей точки и

Решение. Параметрические уравнения контура 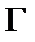есть , или , где действительное изменяется от 0 до . Тогда по теореме 1 получим

.

5 Вычислить .

Решение. Функция аналитична всюду на . Применяя формулу Ньютона-Лейбница, получаем

.

6 Вычислить интеграл , если есть окружность, определяемая уравнением:

а) 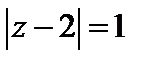; б) ; в) .

Решение. Особыми точками функции будут точки, обращающие в нуль знаменатель, т. е. . Решая уравнение, получим две особые точки , .

а) внутри области , ограниченной окружностью 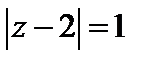, нет особых точек функции , т. е. аналитична в области . В силу теоремы Коши (практическое занятие 3) имеем

;

б) внутри области, ограниченной окружностью , лежит точка . По интегральной формуле Коши имеем:

;

в) в области, ограниченной окружностью , лежат обе особые точки: и . Непосредственно применять интегральную формулу Коши нельзя. Вычислить данный интеграл можно двумя способами.

1 способ Разложим дробь на простейшие:

.

Подставляя в интеграл и применяя интегральную формулу Коши, получим:

.

2 способ Построим окружности и с центрами в точках и малых радиусов таких, чтобы окружности не пересекались и целиком лежали в круге . В трехсвязной области, ограниченной окружностями , и подынтегральная функция аналитична всюду. По теореме Коши для многосвязной области (практическое занятие 3) имеем

.

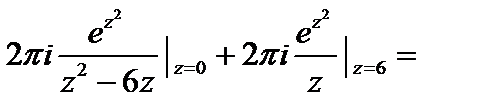
7 Пользуясь интегральной формулой Коши, вычислить интеграл , где окружность обходится в положительном направлении.

Решение. Внутри области, ограниченной окружностью , находится точка , в которой знаменатель функции обращается в нуль.

Перепишем заданный интеграл так

.

Функция является аналитической в круге . Применяя интегральную формулу Коши в точке получим

.

8 Вычислить интегралы

а) ; б) .

Решение. а) особые точки функции , . В области лежит точка .

Преобразуем подынтегральную функцию:

.

Тогда по следствию 2 теоремы 4 получим

;

б) подынтегральная функция является аналитической в области всюду, кроме точки . Функция является всюду аналитической в круге . При по следствию 2 теоремы 4 имеем

.

Так как и , то .

 

 

Индивидуальное задание 4 Вычеты

1 Разложить функции в ряд Лорана в окрестности изолированных особых точек и определить область сходимости полученного ряда.

 

1.1	а) ;	б)
1.2	а) ;	б)
1.3	а) ;	б)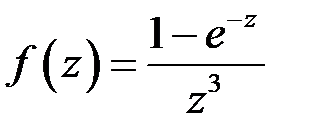
1.4	а) ;	б)
1.5	а) ;	б)
1.6	а) ;	б)
1.7	а) ;	б)
1.8	а) ;	б)
1.9	а) ;	б)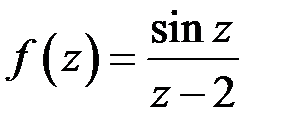
1.10	а) ;	б)
1.11	а) ;	б)
1.12	а) ;	б)
1.13	а)	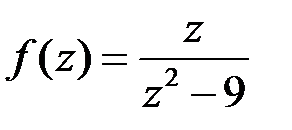б)
1.14	а) ;	б)
1.15	а) ;	б)

 

2 Определить характер особых точек функции на расширенной комплексной плоскости и найти вычеты в этих точках.

2.1	а) ;	б) .
2.2	а) ;	б) .
2.3	а) ;	б) .
2.4	а) ;	б) .
2.5	а) ;	б) .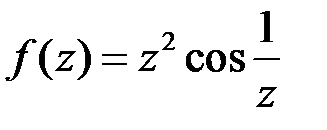
2.6	а) ;	б) .
2.7	а) 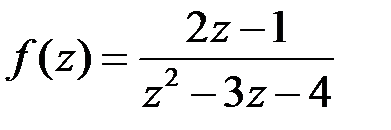;	б) .
2.8	а) ;	б) .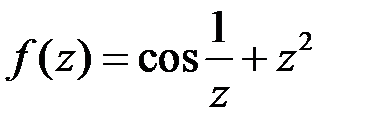
2.9	а) ;	б) .
2.10	а) 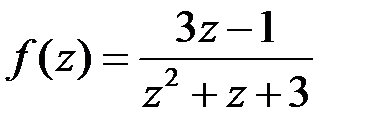;	б) .
2.11	а) ;	б) .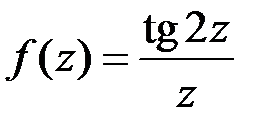
2.12	а) 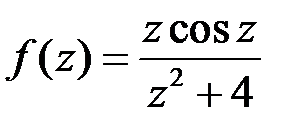;	б) .
2.13	а) ;	б) .
2.14	а) ;	б) .
2.15	а) ;	б) .

Решение типовых примеров:

1 Разложить функцию в ряд Лорана в окрестности особой точки

Решение. Используя основное разложение функции в ряд Маклорена, получим

.

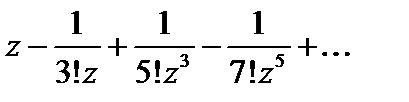Функция является аналитической в кольце .

2 Разложить в ряд Лорана функцию

а) в круге ; б) в кольце ; в) в области .

Решение. Функция имеет две особые точки , . Представим функцию в виде

а) разложение в круге :

.

Ряд для первой функции сходится при условии , т. е. в области , для второй – в области , поэтому ряд для функции сходится в круге ;

б) разложение в кольце :

.

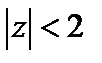Ряд для первой функции сходится, если , т. е. при , для второй функции, если 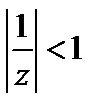, т. е. если , а ряд для функции сходится в кольце ;

в) разложение для :

.

Ряд для первой функции сходится в области 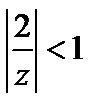, т. е. при 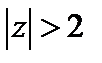, для второй, если , т. е. если , поэтому ряд для функции сходится в области .

3 Разложить функцию в ряд Лорана в окрестности ее особых точек .

Решение. Преобразуем функцию:

.

Разложение в окрестности точки по степеням до ближайшей особой точки 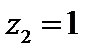(в кольце ) есть:

.

Разложение в окрестности точки по степеням , справедливо в кольце :

.

4 Какую особенность в точке имеет функция ?

Решение. 1 способ Точка является устранимой особой точкой, так как предел в этой точке равен

.

2 способ В окрестности точки разложение в ряд Лорана имеет вид:

= .

Видно, что ряд Лорана в точке не содержит членов с отрицательными степенями, т. е. не содержит главной части. Согласно теореме 3 точка является устранимой особой точкой для функции .

5 Какую особенность в точке имеет функция ?

Решение. 1 способ Имеем:

– если вдоль положительной части действительной оси, то ;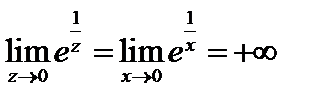

– если 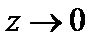вдоль отрицательной части действительной оси, то .

Следовательно, данная функция не имеет предела в точке .

2 способ Разложение в ряд Лорана функции в окрестности точки имеет вид:

.

Видно, что главная часть ряда Лорана содержит бесконечное число членов. Согласно теореме 5 точка является существенно особой точкой.

6 Определить какую особенность в бесконечно удаленной точке имеет функция .

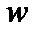Решение. Произведем замену переменной на переменную по формуле . Тогда данная функция принимает следующий вид 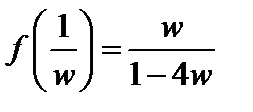. При условии имеет место разложение:

.

Возвращаясь к переменной , имеем:

, .

Видно, что ряд Лорана не содержит правильную часть. Следовательно, точка 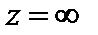является устранимо особой точкой.

7 Найти особые точки и определить их характер для функции .

Решение. Особая точка функции 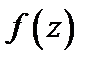есть .

1 способ. Вычислим предел

Значит, является устранимой особой точкой функции.

2 способ. Разложение в ряд Лорана в окрестности точки 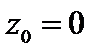имеет вид:

.

Ряд Лорана не содержит главной части, значит по теореме 3 точка 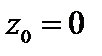есть устранимая особая точка данной функции.

8 Найти особые точки и определить их характер для функции .

Решение. Найдем особые точки функции из условия: .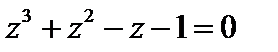

Решая уравнение, получим две особые точки ; .

Найдем предел в точке :

Согласно определению, точка – полюс. Чтобы определить его порядок, представим функцию в виде:

,

где – аналитична в точке и .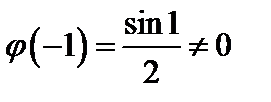

Отсюда по теореме 2 точка – полюс 2-го порядка функции .

Аналогично точка – полюс, поскольку

.

Так как , где – аналитична в точке и , то точка – простой полюс функции

9 Найти особые точки и определить их характер для функции

Решение. Особая точка функции . Так как

, то точка – полюс.

Для функции 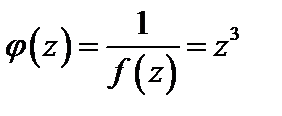точка – нуль третьего порядка, значит, для функции – полюс 3-го порядка.

10 Определить характер особой точки для функции .

Решение. 1 способ Рассмотрим поведение функции на действительной и мнимой осях.

Пусть и при . Пусть и при .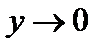

Отсюда следует, что функция не имеет ни конечного, ни бесконечного предела в точке и 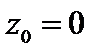– существенно особая точка функции

2 способ Разложим функцию в ряд Лорана в окрестности точки , т. е. в области :

Главная часть ряда Лорана содержит бесконечное число слагаемых, поэтому точка является существенно особой точкой функции

Поделиться: