Бланк результатов расчета

Полный факторный эксперимент

Вариант 1. Задание 1.

Установить зависимость между устойчивостью колонны мартеновской печи (F=y, кН) и определяющими факторами: Х₁- высотой колонны (Н), м; Х₂ -площадью поперечного сечения (S), м²; Х₃ - эксцентриситетом (l₀), мм.

Матрица планирования и результаты экспериментов

№ опыта	Х1	Х2	Х3	Y
	-1	-1	-1
	+1	-1	-1
	-1	+1	-1
	+1	+1	-1
	-1	-1	+1
	+1	-1	+1
	-1	+1	+1
	+1	+1	+1
				79,55
				79,40
				79,10

 

Уравнение регрессии имеет вид:

y=b₀+b₁x₁₊b₂x₂+b₃x₃+b₁₂x₁x₂+b₁₃x₁x₃+b₂₃x₂x₃

Вычислим коэффициенты уравнения регрессии:

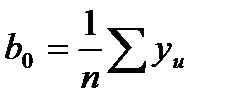
где n=2³= 8.

b₀=(75,90+75,10+75,65+75,15+87,20+84,15+80,55+78,45)/8 = 79,02

b₁=(-75,9+75,10-75,65+75,15-87,20+84,15-80,55+78,45)/8= - 0,81

b₂=(-75,9-75,10+75,65+75,15-87,20-84,15+80,55+78,45)/8= -1,57

b₃=(-75,9-75,10-75,65-75,15+87,20+84,15+80,55+78,45)/8=3,57

b₁₂=(75,9-75,10-75,65+75,15+87,20-84,15-80,55+78,45)/8=0,16

b₁₃=(75,9-75,10+75,65-75,15-87,20+84,15-80,55+78,45)/8= - 1,52

b₂₃=(75,9+75,10-75,65-75,15-87,20-84,15+80,55+78,45)/8=-0,48

Запишем уравнение регрессии с учетом полученных коэффициентов:

y=79,02-0,81X₁-1,57X₂+3,57X₃+0,16X₁X₂-1,52X₁X₃-0,48X₂X₃

Для проверки значимости коэффициентов, нужно установить, выполняется ли условие:

|b_i|≥S_b*t,

Где |b_i|- модуль рассчитанного коэффициента регрессии,

f=n₀-1=3-1=2 –число степеней свободы при количестве опытов в центре плана n₀=3, следовательно t=4.3- табличное значение критерия Стьюдента.

S_b²-дисперсия коэффициентов регрессии,

S_b²=S_B²/n,

S_B²- дисперсия воспроизводимости опытов,

 

Где y_om-значение переменной отклика в центре плана,

n₀=3 – число опытов в центре плана,

Среднее значение переменной отклика в центре плана:

y_ср=(79,55+79,40+79,10)/3=79,35

S_B²=1/(3-1)*(4+9+0)=6,5

S_b²=6,5/8=0,8125

Расчетное значение критерия Стьюдента

t_pi=|b_i|/S_b

Определим значимость коэффициентов, сравнивая расчетное значение критерия Стьюдента с табличным.

t_p0=169>4.3 – коэффициент значим;

t_p1=8,7>4.3 – коэффициент значим;

t_p2=16,8>4.3 – коэффициент значим;

t_p3=23,4>4.3 – коэффициент значим;

t_p12=-2,6<4.3 – коэффициент не значим;

t_p13=-3,2<4.3 – коэффициент не значим;

t_p23=-2,9<4.3 – коэффициент не значим;

Запишем уравнение регрессии с учетом значимых коэффициентов:

y=152,375+7,875X₁+15,125X₂+21,125X₃

Переведем полученное уравнение регрессии в натуральные величины. Для этого воспользуемся исходной таблицей данных.

Уровни факторов	Х1	Х2	Х3
Верхний уровень	3,5
Нижний уровень	3,2	7,8

 

Физические (натуральные) переменные найдем по формулам:

x_i=(X_i-X_i0)/ΔX_i0 ,

где x_{i –} кодированное значение фактора,

X_i – натуральное значение фактора,

ΔX_i0 – интервал варьирования фактора.

Найдем натуральное значение фактора на нулевом уровне:

Х_i0=(X_iB+X_iH)/2,

Где X_iB – значение верхнего фактора,

X_iH – значение нижнего фактора.

X₀₁=(3,5+3,2)/2=3,35;

X₀₂=(11+7,8)/2=9,4;

X₀₃=(12+8)/2=10.

Найдем интервал варьирования факторов:

ΔX₀₁=(3,5-3,2)/2=0,15;

ΔX₀₂=(11-7,8)/2=1,6;

ΔX₀₃=(12-8)/2=2.

Физические (натуральные) переменные примут вид:

Х₁=(Х₁-3,35)/0,15;

Х₂= (Х₂-9,4)/1,6;

Х₃= (Х₃-10)/2.

Преобразуем уравнение регрессии и получим его в натуральных величинах:

y=-217,98+52,5x₁+9,45x₂+10,56x₃.

Уравнение регрессии считается адекватным, если выполняется условие:

F_P≤F_T;

Где F_T – табличное значение критерия Фишера,

F_P – расчетное значение критерия Фишера.

Табличное значение критерия Фишера при уровне значимости α=0,05 зависит от числа степеней свободы дисперсии адекватности

f_ад=n-z,

где n=8,

z=4 – число значимых коэффициентов уравнения регрессии

и числа степеней свободы дисперсии воспроизводимости

f_B=n₀-1,

где n₀=3 – число опытов в центре плана.

f_ад=8-4=4; f_B=3-1=2. F_T=19,247 (по табл).

Расчетное значение критерия Фишера:

F_p=S_ад²/S_B²,

Дисперсия адекватности:

где у_u – экспериментальное значение функции отклика,

у_u – расчетное значение переменной отклика в u-м опыте, определенном при подстановке в уравнение регрессии.

S_ад²=167,5204/4=41,8801,

F_p=41,8801/6,5=6,44.

Выполняется условие 6,44<19.247, т.е. F_P≤F_T, следовательно, полученное уравнение регрессии адекватно.

 

 

Бланк результатов расчета

Исходные данные
Наименование	Обозначение	Единицы измерения	Интервал варьирования	Уровень
Верхний	Нулевой	Нижний
+1		-1
	X1	м	0,15	3,5	3,35	3,2
	X2	м2	1,6		9,4	7,8
	X3	мм

 

Опыты	План	Переменная отклика	Расчеты
X1	X2	X3	yu	yu	(yu-yu)2
	-1	-1	-1		108,21	67,4041
	+1	-1	-1		123,96	9,2416
	-1	+1	-1		138,45	6,5025
	+1	+1	-1		154,2	7,84
	-1	-1	+1		150,45	12,6025
	+1	-1	+1		166,2	3,24
	-1	+1	+1		180,69	5,3361
	+1	+1	+1		196,44	55,3536
					∑(yu-yu)2	167,5204
y0ср=133	SB2=6,5	Sb2=0,8125	t=4,3

 

Коэффициенты уравнения регрессии	b0 152,375	b1 7,875	b2 15,125	b3 21,125	b12 -2,375	b13 -2.875	b23 -2,625
Расчетное значение критерия Стьюдента tp	t0	t1   8,7	t2   16,8	t3   23,4	t12   -2,6	t13   -3,2	t23   -2,9
Проверка значимости	+	+	+	+	-	-	-
Sад2=41,8801
Fp=6,44 FT=19,247 Модель адекватна
Рассчитанное уравнение регрессии
Кодированное	y=152,375+7,875X1+15,125X2+21,125X3
Натуральное	y=-217,98+52,5x1+9,45x2+10,56x3